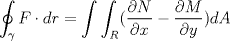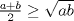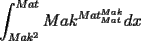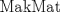|
|
|
|
|
|
|
  |
 Sep 10 2008, 02:07 PM Sep 10 2008, 02:07 PM
Publicado:
#1
|
|
|
Dios Matemático Supremo Grupo: Baneado Mensajes: 3.360 Registrado: 11-March 08 Miembro Nº: 16.617 |
  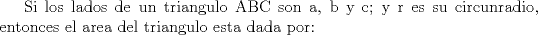 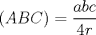 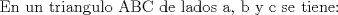 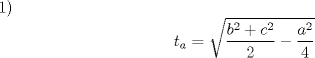 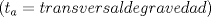 ![TEX: 2)$$<br />b_\alpha = \sqrt {\frac{{bc}}<br />{{\left( {b + c} \right)^2 }}\left[ {\left( {b + c} \right)^2 - a^2 } \right]} <br />$$](./tex/c4ea7a5d2dd90683ea366fef350254bb.png) 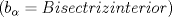 ![TEX: 3)$$<br />b_{\alpha '} = \sqrt {\frac{{bc}}<br />{{\left( {c - b} \right)^2 }}\left[ {a^2 - \left( {c - b} \right)^2 } \right]} <br />$$](./tex/55456e45872af69dfcbdf1bfe673b325.png) 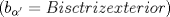    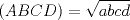 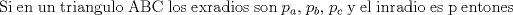 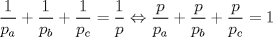 |
|
|
|
 Sep 11 2008, 08:58 PM Sep 11 2008, 08:58 PM
Publicado:
#2
|
|
 Staff Fmat Grupo: Moderador Mensajes: 1.185 Registrado: 29-October 05 Desde: Santiago, Chile Miembro Nº: 352 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
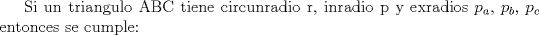 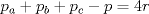 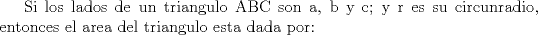 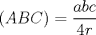 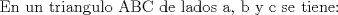 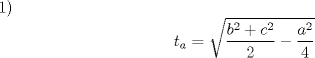 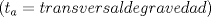 ![TEX: 2)$$<br />b_\alpha = \sqrt {\frac{{bc}}<br />{{\left( {b + c} \right)^2 }}\left[ {\left( {b + c} \right)^2 - a^2 } \right]} <br />$$](./tex/c4ea7a5d2dd90683ea366fef350254bb.png) 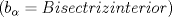 ![TEX: 3)$$<br />b_{\alpha '} = \sqrt {\frac{{bc}}<br />{{\left( {c - b} \right)^2 }}\left[ {a^2 - \left( {c - b} \right)^2 } \right]} <br />$$](./tex/55456e45872af69dfcbdf1bfe673b325.png) 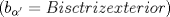 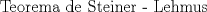 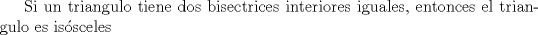  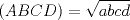 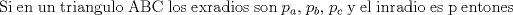 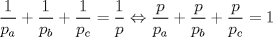 Sería bueno que entregaras algunas demostraciones de estas fórmulas (podrían estar erradas), o que algún otro usuario del foro lo haga. De todas formas se agradece el aporte Saludos. -------------------- "He looks rather ill, but he looks all over the genius he was" (G. H. Hardy)
"A mathematician is a device for turning coffee into theorems" (Paul Erdös) |
|
|
|
 Sep 20 2008, 07:45 PM Sep 20 2008, 07:45 PM
Publicado:
#3
|
|
 Matemático Grupo: Usuario FMAT Mensajes: 55 Registrado: 3-May 06 Desde: Location Unknow Miembro Nº: 1.018 Nacionalidad:  Universidad:  Sexo:  |
junto con dar algunos teoremas mas,q nos ayudarn para lo siguiente, dare algunas dem(de las q me acuerdo) de las teoremas puestos por vivanco. se q talves la dem de algunso teoremas no son como muy elegantes q digamos...pero weno algo es algo xd
primero dare la de la medida de la bisectriz y de la tranversal de gravedad... para su demostraciones rapi2 y baratas usaremas el teorema de stewart(stw)( http://www.fmat.cl/index.php?showtopic=9371). dem. de la tranversal de gravedad(voy a pedir prestado la foto de Krizalid, del topic de stw) Usando stw  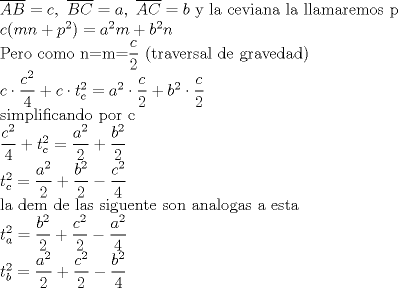 Dem de la bisectrices (para ello usaremas el teoremas de la bisectrices.. creo q asi se llma) Sabemos por el t de las bisec. interior q ![TEX: $n=\dfrac{ac}{a+b} \ , m=\dfrac{bc}{a+b}$\\<br />$c\left(\dfrac{abc^2}{(a+b)^2}+b_\gamma^2\right)=\dfrac{a^2bc}{a+b} + \dfrac{b^2ac}{a+b}$\\<br />$\text{simplificando por c}$\\<br />$b_\gamma^2=\dfrac{a^2bc+b^2ac}{a+b}-\dfrac{abc^2}{(a+b)^2}$\\<br />$b_\gamma^2=\dfrac{ab(a+b)}{a+b}-\dfrac{abc^2}{(a+b)^2}$\\<br />$b_\gamma^2=ab-\dfrac{abc^2}{(a+b)^2}$\\<br />$b_\gamma^2=ab\left(1-\dfrac{c^2}{(a+b)^2}\right)$\\<br />$b_\gamma^2=\dfrac{ab}{(a+b)^2}[(a+b)^2-c^2]$\\<br />$\text{analogamente a esta salen}$\\<br />$b_\alpha^2=\dfrac{bc}{(b+c)^2}[(b+c)^2-a^2]$\\<br />$b_\beta^2=\dfrac{ca}{(c+a)^2}[(c+a)^2-b^2]$](./tex/46b9b69d822420511eb854bd216f4c86.png) formula del area en funcion de sus lados y el radio de la circunferencia circuncrita ( r )  geo1231.PNG ( 12.11k )
Número de descargas: 0
geo1231.PNG ( 12.11k )
Número de descargas: 0  t3.PNG ( 8.21k )
Número de descargas: 0
t3.PNG ( 8.21k )
Número de descargas: 0Areas en funcion del radio de la circunferencia incrita Sea   t4.PNG ( 10.23k )
Número de descargas: 0
t4.PNG ( 10.23k )
Número de descargas: 0Area en funcion de los radios de laa circunferencias excinscritas( 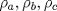 ) )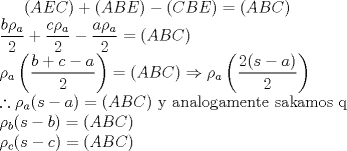 teninedo encuenta las formulas de las areas demotraremos lo siguente: 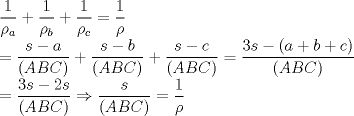 ![TEX: \noindent$\rho_a+\rho_b+\rho_c+\rho=4r$\\<br />$=\dfrac{(ABC)}{s-a}+\dfrac{(ABC)}{s-b}+\dfrac{(ABC)}{s-c}+\dfrac{(ABC)}{s}$\\<br />$=\dfrac{(ABC)[s(s-b)(s-c)+s(s-b)(s-a)+s(s-a)(s-c)-(s-a)(s-b)(s-c)]}{s(s-a)(s-b)(s-c)}$\\<br />$=\dfrac{(ABC)[s(s-c)[s-b+s-a]+(s-a)(s-b)[s-(s-c)]]}{(ABC)^2}$(por heron)\\<br />$=\dfrac{s(s-c)c+(s-a)(s-b)c}{(ABC)}$\\<br />$=\dfrac{c[s^2-cs+s^2-bs-as+ab]}{(ABC)}$(dps de resolver)\\<br />$=\dfrac{c[2s^2-s(a+b+c)+ab]}{(ABC)}$\\<br />$=\dfrac{c[ab]}{(ABC)} \Rightarrow \dfrac{cab}{(ABC)}=4r $\\](./tex/092de7acc1619b312426e4a087a7047a.png) multiplicando las formulas de las areas de recien tenemos 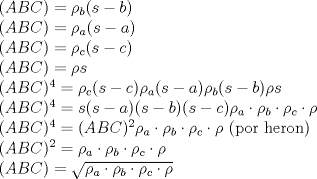 Bueno eso por ahora pd: dem de heron no puso , pues es muy conocida(creo q estas tmb) pero weno. -------------------- "Dios creo los números naturales, todo lo demás es obra del hombre"
Leopold Kronecker Estudiante de Matemagica , de por vida Curriculum : |
|
|
|
 Sep 20 2008, 08:54 PM Sep 20 2008, 08:54 PM
Publicado:
#4
|
|
 Dios Matemático Supremo Grupo: Moderador Mensajes: 590 Registrado: 14-October 07 Miembro Nº: 11.310 Colegio/Liceo:  Universidad:  Sexo:  |
hay un ejercicio relacionado con esas formulas, eso creo porque piden la distancia entre el circuncentro y el incentro
-------------------- |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 9th April 2025 - 04:11 AM |