|
|
|
|
|
|
|
  |
 Feb 22 2010, 12:10 AM Feb 22 2010, 12:10 AM
Publicado:
#1
|
|
|
Principiante Matemático Grupo: Usuario FMAT Mensajes: 7 Registrado: 21-February 10 Miembro Nº: 66.023 |
**Reposteado/movido en/a la sección correcta del foro.**
Hola! Soy nuevo acá, pero me encanta el espíritiru del foro. Soy de la Universidad SImón Bolívar de Venezuela. En fin, estoy apenas empezando con series, y me doy cuenta que me cuesta muchsimo determinar a qué otra serie comprar alguna para simplificar el trabajo de la determinación de su convergencia. No sé si alguien tiene algunos consejos o tips para hallar algo a qué comparar, porque estoy sentado haciendo ejercicios y no doy con nada! (excepto para polinomios). Estos son algunos que he intentado y no tengo ni idea: ![TEX: \[1)\sum{\frac{{({\cos n\ })}^2}{3^n}}\ \ \ \ \ \ \ \ \ ,\ \ \ \ \ \ \ \ \ \ \ \ 2)\sum{\frac{{\ln n\ }}{e^n}}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ ,\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 3)\sum{\frac{1}{3+5^n}}\]](./tex/9a16d2c28b2ee849505abe9293d0a9dd.png) Gracias y disculpen la molestia! Mensaje modificado por jahd5000 el Feb 22 2010, 12:11 AM |
|
|
|
 Feb 22 2010, 12:29 AM Feb 22 2010, 12:29 AM
Publicado:
#2
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.818 Registrado: 21-December 06 Miembro Nº: 3.434 |
Es una consulta por tema, pero te lo dejo pasar esta vez.
Por ejemplo, la tercera serie que pones, si n es muy grande, tienes que 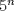 es asquerosamente mas grande que 3, y entonces la serie es parecida a la que tiene como término general es asquerosamente mas grande que 3, y entonces la serie es parecida a la que tiene como término general 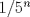 , asi que probablemente sea bueno comparar con esa. , asi que probablemente sea bueno comparar con esa.La segunda serie creo que sale mas facil por criterio del cuociente. Para la primera, 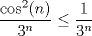 y cae altiro. y cae altiro.
-------------------- |
|
|
|
 Feb 22 2010, 01:56 AM Feb 22 2010, 01:56 AM
Publicado:
#3
|
|
|
Principiante Matemático Grupo: Usuario FMAT Mensajes: 7 Registrado: 21-February 10 Miembro Nº: 66.023 |
Es una consulta por tema, pero te lo dejo pasar esta vez. La segunda serie creo que sale mas facil por criterio del cuociente. si bueno, la postee primeramente no por las series sino por pedir consejo para sabes a que comparar, y segundo porque en verdad son lo más basico y a modo de ejemplo, pero de verdad mil gracias por aclarar cada una. Ahora para la segunda, no puedo servirme del criterio del cociente porque los ejericios sugeridos, estos entre ellos, estan para elaborarse sólo con las herramientas de comparacion inicialmente y luego integral o propiedades básicas de las series (geometrica, serie p, telescopica y armonica) |
|
|
|
 Feb 22 2010, 07:33 AM Feb 22 2010, 07:33 AM
Publicado:
#4
|
|
 Staff FMAT Grupo: Super Moderador Mensajes: 8.124 Registrado: 21-May 06 Miembro Nº: 1.156 Nacionalidad:  Sexo:  |
En la tercera, si sólo deseas usar comparación, toma en cuenta de que para
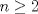 (en general las series parten en (en general las series parten en 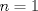 pero como el logaritmo de la unidad es cero, vale la pena partir en 2), es pero como el logaritmo de la unidad es cero, vale la pena partir en 2), es 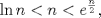 de tal manera que de tal manera que 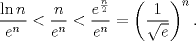 Eventualmente tu serie es convergente comparada con la geométrica de término general 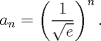 ----- En verdad encuentro algo innecesario poner problemas en donde las cotas no resulten tan fáciles de hallar, ahí es cuando viene adecuado aplicar comparación con paso al límite, criterio de la raíz, del cuociente, de la integral, etc. Ahora bien, para la primera, siempre es bueno tener un manejo de variadas desigualdades, y una de las más importantes es la del acotamiento del coseno, pues 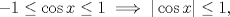 y luego como ambos miembros son positivos, tenemos que y luego como ambos miembros son positivos, tenemos que 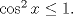 Esto usó DTK la convergencia concluye rápidamente de la serie geométrica. Esto usó DTK la convergencia concluye rápidamente de la serie geométrica.Por otra parte, para la 3era. es todo un manejo tuyo, tú acotas como quieres, pues sabes que para cada todo 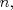 (en particular para (en particular para 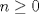 ), es claro que es ), es claro que es 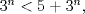 luego luego 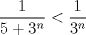 y de nuevo concluyes usando comparación directa con la serie geométrica. (De hecho, por algo se denota por comparación directa, en donde las cotas no son difíciles de hallar.) y de nuevo concluyes usando comparación directa con la serie geométrica. (De hecho, por algo se denota por comparación directa, en donde las cotas no son difíciles de hallar.) |
|
|
|
 Feb 22 2010, 06:04 PM Feb 22 2010, 06:04 PM
Publicado:
#5
|
|
|
Principiante Matemático Grupo: Usuario FMAT Mensajes: 7 Registrado: 21-February 10 Miembro Nº: 66.023 |
Si!, Gracias. Lo del coseno cuadrado siendo entre 0 y 1 ya me lo habia figurado, y el tercero ciertamente es sencillo. Pero ya como que le voy agarrando más a esto, me sirven mucho sus explicaciones. Mil gracias!
Kriz, me gusta mucho to signature de PS3! las hiciste tu? porque entiendo que hay muchos sitios que te ofrecen urls de imagenes gif generadas con los labels que tu escojas, pero me extraña q el tuyo no tenga algún link! Mensaje modificado por jahd5000 el Feb 22 2010, 06:12 PM |
|
|
|
 Feb 22 2010, 06:27 PM Feb 22 2010, 06:27 PM
Publicado:
#6
|
|
 Staff FMAT Grupo: Super Moderador Mensajes: 8.124 Registrado: 21-May 06 Miembro Nº: 1.156 Nacionalidad:  Sexo:  |
No para nada, no me acuerdo dónde la robé.
Me alegro que te sirva la ayuda, saludos. |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 9th April 2025 - 07:01 AM |











