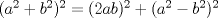Regularidades en Tríos Pitagóricos

Foro fmat.cl > Sector Preparación PSU - Construyendo tu camino al éxito !! > Contenidos > Geometría

2 Páginas:

1 2 >

Regularidades en Tríos Pitagóricos, Es bueno saber esto

Opciones

GmHernan Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 26 2010, 11:26 PM Publicado: #1
Maestro Matemático Grupo: Team Ensayos FMAT Mensajes: 114 Registrado: 4-March 09 Desde: Ñuñoa Miembro Nº: 44.042 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Otro buen post sobre nuestro amigo Pitágoras. $TEX: Los tríos pitagoricos corresponden a numeros naturales enteros que se encuentran en los lados del tríangulo rectángulo y cumpliendo con el teorema de Pitágoras. $ a^2 + b^2 = c^2 $<br />Algunos tríos pitagóricos son $ 3-4-5, 6-8-10, 9-40-41 $, y asi enternamente podría mencionar.<br />La pregunta es, ¿estos trios son por azar?. ¿Si son por azar, tendremos que aprendernos todos de memoria?<br />La respuesta es muy sencilla, en la matemática muy pocas son al azar y realmente suena tonto y absurdo aprenderse tantos tríos. Existe unas fórmulas que expresan estos tríos. La primera es<br /><br />$ \displaystyle a, \frac {(a^2-1)}{2}, \frac {(a^2+1)}{2} $ Solo para impares $ > que 1 $ <br /><br /> <br /><br /><br />Donde $a$ corresponde al cateto menor ,$ \frac {(a^2-1)}{2}$ al otro cateto y $ \frac {(a^2+1)}{2} $ a la hipotenusa. El porque de esto es fácil de explicar, solo basta realizar esto<br /><br />$ \displaystyle (a)^2 + (\frac {(a^2-1)}{2} )^2 = c^2 $<br /><br /><br />$ \displaystyle a^2 + \frac {a^4-2a^2+1}{4} = c^2 $<br /><br /><br />$ \displaystyle \frac {a^4+2a^2+1}{4} = c^2 $<br /><br /><br />$ \displaystyle \frac {(a^2+1)}{2} = c$<br /><br />Y como $ a^2 + 1 $ para que sea divisible por $ 2 $, ya que los trios trabajan con números enteros y naturales, $a$ debe ser $2n+1$ desde $ n=1$, ya que un impar al cuadrado da impar y mas $1$ da un valor par.<br /><br />Ejemplo, $ 9,40,41 $. $ 9 $ es cateto menor, y por fórmula pitagoras sería. <br /><br /><br />$ \displaystyle \frac {9^2 - 1}{2} = 40 $<br /><br /><br />$ \displaystyle \frac {9^2 + 1}{2} = 41 $<br /><br />Comprobando<br />$ 9^2 + 40^2 = 41 ^2 $<br /><br /><br />$ 81 + 1600 = 1681 $<br /><br />La segunda fórmula corresponde a :<br /><br /><br /><br />$ \displaystyle a, \frac {a^2}{4} - 1, \frac {a^2}{4} + 1 $ Sola para valores pares $ > 2 $<br /><br /><br /><br />Teorema de Aquita (no estoy seguro del nombre, sorry)<br /><br /><br />Donde $a$ corresponde al cateto menor, $\frac {a^2}{4} - 1 $ al otro cateto y $\frac {a^2}{4} +1$ a la hipotenusa.<br /><br />La explicación es analoga a la anterior, pero lo hare de otra forma. <br />$c$ cateto menor, $a$ valor a comprobar <br />$ $TEX: <br />$ \displaystyle ©^2 = (\frac {a^2}{4} - 1)^2 - (\frac {a^2}{4} +1)^2 $ (aplicando suma por diferencia)<br /><br /><br />$ \displaystyle ©^2 = [(\frac {a^2}{4} - 1) + (\frac {a^2}{4} +1)][(\frac {a^2}{4} - 1) - (\frac {a^2}{4} +1)] $<br /><br /><br />$ \displaystyle ©^2 = {a^2} $ <br /><br />Y como $a^2$ para ser divisible por 4, debe ser $2n+2$ desde $n=1$, puesto que par al cuadrado dara par, y debe ser mayor que 2 ya que en la fórmula del cateto mas grande, quedaria en 0<br />Ejemplo, $ 10,24,26 $. $ 10 $ es cateto menor, y por fórmula pitagoras sería. <br /><br /><br />$ \displaystyle \frac {10^2 }{2}-1 = 24 $<br /><br /><br />$ \displaystyle \frac {10^2}{2}+1 = 26 $<br /><br />Comprobando<br /><br /><br />$ 10^2 + 24^2 = 26 ^2 $<br /><br /><br />$ 100 + 576 = 676 $<br /><br /><br />$ Espero que les sirva harto, puesto que me demore mucho en demostrarlo Saludos, sirve para sacar triangulos con sólo un cateto o sólo una hipotenusa y han salido ejercicio asi Por si acaso, ahi el link del porque use suma por diferencia http://www.fmat.cl/index.php?showtopic=55306 Pd: un dia aburrido en clases lo saque y pense que era algo nuevo, pero lo vi en un libro y me di cuenta que america ya había sido decubierta Sorry por la redacción, estaba cag* de sueño Mensaje modificado por GmHernan** el Jan 27 2010, 04:13 PM -------------------- Son unos loquillos QUOTE(toto Usorno @ Nov 13 2010, 07:54 PM) Loco, tomate otro año no más erís joven no le hagai caso a esta manga de ñoños culiaos que serían incapaces de perder años porq no tendrían de que vanagloriarse (sus únicos logros son los académicos). Sigue adelante no más, encuentra tu vocación y si son 10 años los que tenís q esperar, esperalos... en Europa los hue.ones salen del colegio y salen a recorrer el mundo como dos años y de ahí se meten a la universidad... nadie te apura socio... SE FELIZ QUOTE(MatematicoPrincipiante @ Jul 17 2012, 05:18 PM) .......... no importa cual sea la identidad de kaissa...estamos en un foro de matemáticas, no en facebook, importa un pico si kaissa es hombre, mujer, buena para culear, etc., .......... QUOTE(salvador.augusto allende @ Jul 24 2012, 10:19 PM) .......... pero estas escuelas qls valen callampa, lo unico bueno que tienen son las mansas perras, en otras palabras solamente irias a la u a remojar el pate.... QUOTE(Maxooon @ Mar 6 2012, 06:57 AM) Santiago lindo, santiago hermoso, me encanta tu aroma a smog por las mañanas y el sonido de los claxon por las tardes, tu gente mal genio y apurada, tu locomocion congestionada, y que todas las noches me hagas cerrar mi casa con candados, llaves, pestillos y alarmas. QUOTE(MatematicoPrincipiante @ Jul 17 2012, 05:18 PM) .......... no importa cual sea la identidad de kaissa...estamos en un foro de matemáticas, no en facebook, importa un pico si kaissa es hombre, mujer, buena para culear, etc., .......... QUOTE(//Whiplash// @ Jun 1 2010, 11:44 PM) Las mujeres también tenemos derechos QUOTE(salvador.augusto allende @ Jul 24 2012, 10:19 PM) .......... pero estas escuelas qls valen callampa, lo unico bueno que tienen son las mansas perras, en otras palabras solamente irias a la u a remojar el pate.... QUOTE(Maxooon @ Mar 6 2012, 06:57 AM) Santiago lindo, santiago hermoso, me encanta tu aroma a smog por las mañanas y el sonido de los claxon por las tardes, tu gente mal genio y apurada, tu locomocion congestionada, y que todas las noches me hagas cerrar mi casa con candados, llaves, pestillos y alarmas. QUOTE(Kaissa @ Jan 3 2013, 06:12 PM) Dios! Señor! qué hemos hecho para merecer leer esto!!!! Hubiera tenido más sentido decir "un thread del año pasado" Voy a enumerar un poco: 1- lógica fail. 2- redacción fail. 3- gramática fail. Me vas a disculpar, estimado coquitao pero le voy a sacar un screenshot a esto y lo voy a nominar al "post fmat del año" (pero aún estoy en la indecisión de que sea 2012 o 2013 :( )

Nabodorbuco Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 27 2010, 08:08 AM Publicado: #2
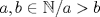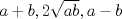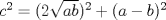Dios Matemático Supremo Grupo: Team Ensayos FMAT Mensajes: 513 Registrado: 25-April 08 Desde: CSMC Miembro Nº: 21.189 Nacionalidad: Colegio/Liceo: Sexo:	Aportando a lo escrito por GmHernan Otro metodo para encontrar trios pitagoricos, esta vez con dos numeros $TEX: $a, b \in \mathbb{N} /a>b$$ seria $TEX: $a+b,2\sqrt{ab},a-b$$ , donde $TEX: $a+b$$ es la hipotenusa. 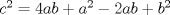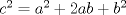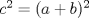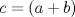$TEX: $c^{2}=(2\sqrt{ab})^{2}+(a-b)^{2}$$ $TEX: $c^{2}=4ab+a^{2}-2ab+b^{2}$$ $TEX: $c^{2}=a^{2}+2ab+b^{2}$$ $TEX: $c^{2}=(a+b)^{2}$$ $TEX: $c=(a+b)$$ Resultando 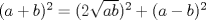$TEX: $(a+b)^{2}=(2\sqrt{ab})^{2}+(a-b)^{2}$$ una manera alternativa para los que no gustan de raices $TEX: $(a^{2}+b^{2})^{2}=(2ab)^{2}+(a^{2}-b^{2})^{2}$$ -------------------- FunGeometry SIEMPRE CON LAS MEJORES INTENCIONES DE AYUDAR. ATTE. NABODORBUCO EL TERCER OJO GoGeometry LA IDEA ES QUE NO ESPERES QUE FMAT RESUELVA TUS TAREAS, ESCRIBE SIEMPRE CUALES SON TUS INQUIETUDES

Phi Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 27 2010, 09:26 AM Publicado: #3
Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 161 Registrado: 11-October 07 Miembro Nº: 11.187 Nacionalidad: Sexo:	wena.. me recuerda el colegio esto.. un dia un profe me lo hizo como reto.. y me dijo que uno de sus otros alumnos lo habia hecho en 7 dias.. bueno la cosa es que me demore como 15 minutos xd.. aun recuerdo la cara del profe.. aunq el me cae muy bien.. buen aporte en todo caso =) .. saludos --------------------

fabiannx15 Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 27 2010, 11:03 AM Publicado: #4
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.169 Registrado: 11-June 08 Desde: rancagua Miembro Nº: 26.922 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	lo habia leido por ahi... pero nunca le puse antencion ahora kaxe gracias -------------------- Richard Fabian Jerez Ex alumno del Liceo Oscar Castro 4ºL matemático Estudiante Ingeniería Civil Mecánica USM ¿Necesitas ayuda para la psu y no tienes dinero?: Agrega a logratus850@hotmail.com y comienza a preguntar! Somos un grupo de universitarios dispuestos a ayudarte de manera gratuita para que logres tus sueños, todos tuvimos como promedio más de 800 puntos en la PSU. Team PSU 2010!! Únete! [color="#000080"][/color]

Anis Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 27 2010, 02:22 PM Publicado: #5
Maestro Matemático Grupo: Team Ensayos FMAT Mensajes: 102 Registrado: 22-October 08 Desde: MAIPU Miembro Nº: 36.770 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	por lo menos en mi coleee nunka lo vi xD ! wuen aporte gracias -------------------- Anis rosaditaaaaaaaa !!!! sumateee con tu firma !!! jojo

Kaissa Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 27 2010, 03:46 PM Publicado: #6
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad: Colegio/Liceo: Sexo:	de acuerdo esta bonito... pero tengo un problema con tu explicacion: La Redaccion xd ojala arreglaras eso. comentar tambien que en el sector olimpico de fmat y tambien en mathlinks este tema es arduamente tratado, entre otras cosas se puede demostrar que si x, y z son un trio pitagorico de enteros entoncces xyz es divisible por 60; en fin. tambien hay una formula explicita para hallar TODOS los trios pitagoricos que existen, sin distincion alguna. (obviamente los importantes son aquellos en que mcd(x,y,z)=1) -------------------- Este es un extracto de Qué es fmat by Kenshin. La pregunta para ti estimado(a) lector(a) es... ¿Qué haces tu para que ésto se cumpla?

felper Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 27 2010, 03:54 PM Publicado: #7
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.767 Registrado: 21-January 08 Desde: Santiago - Ancud Miembro Nº: 14.865 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Scott Loomis redactó un libro en el que compilaba 367 demostraciones del teorema de Pitágoras. En él también aparecen muchas construcciones de tríos Pitagóricos. Si alguien quiere profundizar en este tema, puede buscar aquel libro. Buen aporte, GmHernan. -------------------- Estudia para superarte a ti mismo, no al resto.

sebaxbkn Ver Perfil del Miembro Ver los mensajes de este miembro	Sep 23 2011, 02:22 PM Publicado: #8
Principiante Matemático Destacado Grupo: Usuario FMAT Mensajes: 16 Registrado: 7-August 08 Miembro Nº: 31.682 Nacionalidad: Colegio/Liceo: Sexo:	Uhh que bkn! No lo conocía, me ayudaste a hacer una tareas, muchas gracias!!

andreanthua Ver Perfil del Miembro Ver los mensajes de este miembro	Sep 23 2011, 02:44 PM Publicado: #9
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.525 Registrado: 13-July 10 Desde: Santiago, Chile Miembro Nº: 74.135 Nacionalidad: Universidad: Sexo:	Gracias a esto no tengo que aprenderme los tríos pitagóricos. Gracias, aportazo!. -------------------- Stay hungry. Stay foolish ahorroClicks

Legition Rompedi... Legition Rompediskoteqa Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 28 2012, 11:31 PM Publicado: #10
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.566 Registrado: 20-June 11 Desde: Region del Maule Miembro Nº: 90.738 Sexo:	3,4,5 5,12,13 8,15,17 9,40,41 vale me ahorraste aprendermelos -------------------- Actualmente en Ingenieria Industrial y en 3er año Ingeniería Civil Mecánica. From my personal life: I highly recommend this video Click Here!** Es altamente deseable tener aptitud para la quimica(termodinámica), la programación, alta comprensión de un problema y planteamiento del mismo, y tener resiliencia al estudiar Ingenieria Civil Industrial. Civil Industrial es en gran parte saber levantar(modelar problemas) procesos logísticos. Puedo dar fe que la Universidad Nacional Andres Bello está adelante de varias U'es Regionales(Calidad similar a la UTAL). Realidad universidades del mundo (18:30): Youtube Quiten Filosofia, Musica y Religión del Curriculum de la Media!! No es recomendado trabajar/colaborar entre matemáticos en general. En general, y a menos que Chile gaste mínimo 2% PIB en I+D, quedarse a investigar en el país, es matarse académicamente. Como recomendación Brasil es un pais muy adelantado en investigación versus AL. Gasto 2023: 0,34%.

« Posterior · Geometría · Anterior »

2 Páginas:

1 2 >

2 usuario(s) está(n) leyendo esta discusión (2 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 23rd November 2024 - 03:09 PM