|
|
|
|
|
|
|
  |
 Jan 26 2010, 01:34 PM Jan 26 2010, 01:34 PM
Publicado:
#1
|
|
|
Dios Matemático Supremo Grupo: Baneado Mensajes: 3.360 Registrado: 11-March 08 Miembro Nº: 16.617 |
Encontrar las/la solucion mediante cualquier herramienta que desee
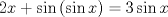
Mensaje modificado por xdanielx el Jan 26 2010, 01:34 PM |
|
|
|
 May 5 2018, 05:47 PM May 5 2018, 05:47 PM
Publicado:
#2
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.566 Registrado: 20-June 11 Desde: Region del Maule Miembro Nº: 90.738 Sexo:  |
Quizas estoy complejizandolo, no creo :/
Le doy un poco de avance ![TEX: \[\begin{gathered}<br /> 2 + \cos (\sin x)\cos x = 3\cos x \hfill \\<br /> (\cos (\sin x))'\cos x + \cos (\sin x)\sin x = - 3senx \hfill \\<br /> - \sin (\sin x){\cos ^2}x + \cos (\sin x)\sin x = - 3senx \hfill \\<br /> - \sin (\sin x)(1 - {\sin ^2}x) + \cos (\sin x)\sin x = - 3senx \hfill \\<br /> \sin (\sin x) + \sin (\sin x)({\sin ^2}x) + \sin x\cos (\sin x) = - 3\sin x \hfill \\<br /> \sin (\sin x) + \sin (\sin x)({\sin ^2}x) + \sin x(\sqrt {1 - {{\sin }^2}(\sin x} ) = - 3\sin x \hfill \\ <br />\end{gathered} \]](/tex-image/8671faf901ac8b25a8461e0e1513829c.png) ![TEX: \[\begin{gathered}<br /> u = \sin x \hfill \\<br /> \sin u + \sin (u){u^2} + u\sqrt {1 - {{\sin }^2}(u)} = - 3u \hfill \\<br /> u\sqrt {1 - {{\sin }^2}(u)} = - 3u - \sin u - \sin (u){u^2} \hfill \\ <br />\end{gathered} \]](/tex-image/ad28002618fe07ddcac88d27c8f65764.png) ![TEX: \[\begin{gathered}<br /> \sin (u)(1 - {u^2}) = - 3u + u\sqrt {1 - {{\sin }^2}(u)} \hfill \\<br /> \sin (u)(1 - {u^2}) = - 3u(1 - \sqrt {1 - {{\sin }^2}(u)} ) \hfill \\<br /> {\text{Arreglado error signo al derivar cos en 2da linea y el menos en 4ta linea}} \hfill \\ <br />\end{gathered} \]](/tex-image/3a7b8258a25365f5d0da1887326feecd.png)
Mensaje modificado por Legition Rompediskoteqa el May 6 2018, 03:36 PM -------------------- Actualmente en Ingenieria Industrial y en 3er año Ingeniería Civil Mecánica.
From my personal life: I highly recommend this video Click Here! Es altamente deseable tener aptitud para la quimica(termodinámica), la programación, alta comprensión de un problema y planteamiento del mismo, y tener resiliencia al estudiar Ingenieria Civil Industrial. Civil Industrial es en gran parte saber levantar(modelar problemas) procesos logísticos. Puedo dar fe que la Universidad Nacional Andres Bello está adelante de varias U'es Regionales(Calidad similar a la UTAL). Realidad universidades del mundo (18:30): Youtube Quiten Filosofia, Musica y Religión del Curriculum de la Media!! No es recomendado trabajar/colaborar entre matemáticos en general. En general, y a menos que Chile gaste mínimo 2% PIB en I+D, quedarse a investigar en el país, es matarse académicamente. Como recomendación Brasil es un pais muy adelantado en investigación versus AL. Gasto 2023: 0,34%.  |
|
|
|
 Jun 15 2018, 08:10 PM Jun 15 2018, 08:10 PM
Publicado:
#3
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 947 Registrado: 28-September 07 Desde: Santiago Miembro Nº: 10.639 Nacionalidad:  Universidad:  Sexo:  |
A simple vista, una solución es x=0 (esto demuestra por lo menos la existencia de por lo menos una solución jaja).
Se me ocurrió algo muy flaite, pero igual no más xd, pa que alguien lo corrija y lo modifique para resolverlo. Considere 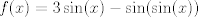 . El objetivo se reduce a resolver . El objetivo se reduce a resolver 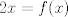 . .La función f es continua y periódica. Encontremos los puntos críticos de f. 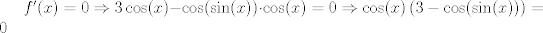 osea 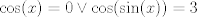 La segunda es vacía. La primera implica que 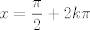 o o 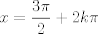 Entonces tenemos que 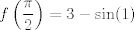 y y 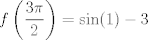 Así, para todo x real, 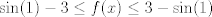 Pero como queríamos resolver 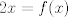 , entonces imponemos , entonces imponemos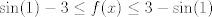 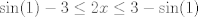 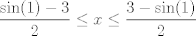 Buscamos así soluciones para x en ese intervalo. Aprovechando un post que hice hace unas semanas, usaremos el método de la secante para buscar una solución a la ecuación 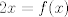 , que es equivalente a encontrar los ceros de la función , que es equivalente a encontrar los ceros de la función 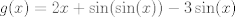 . Subo excel con las iteraciones. Ojo que excel trabaja con punto flotante, pero filo xd. . Subo excel con las iteraciones. Ojo que excel trabaja con punto flotante, pero filo xd.En la primera iteración encontramos un cero de g(x), la cual converge a exactamente 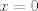 , la cual fue encontrada al principio al ojo. , la cual fue encontrada al principio al ojo.Por la estructura de la ecuación, tengo toda la tincada que es la única solución. Sólo faltaría demostrar la unicidad. Mensaje modificado por Laðeralus el Jun 15 2018, 08:15 PM
Archivo(s) Adjunto(s)
|
|
|
|
 Jun 15 2018, 10:31 PM Jun 15 2018, 10:31 PM
Publicado:
#4
|
|
 Maestro Matemático Grupo: Usuario FMAT Mensajes: 110 Registrado: 8-February 16 Miembro Nº: 143.585 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Off-topic
Quizas estoy complejizandolo, no creo :/ Le doy un poco de avance ![TEX: \[\begin{gathered}<br /> 2 + \cos (\sin x)\cos x = 3\cos x \hfill \\<br /> (\cos (\sin x))'\cos x + \cos (\sin x)\sin x = - 3senx \hfill \\<br /> - \sin (\sin x){\cos ^2}x + \cos (\sin x)\sin x = - 3senx \hfill \\<br /> - \sin (\sin x)(1 - {\sin ^2}x) + \cos (\sin x)\sin x = - 3senx \hfill \\<br /> \sin (\sin x) + \sin (\sin x)({\sin ^2}x) + \sin x\cos (\sin x) = - 3\sin x \hfill \\<br /> \sin (\sin x) + \sin (\sin x)({\sin ^2}x) + \sin x(\sqrt {1 - {{\sin }^2}(\sin x} ) = - 3\sin x \hfill \\ <br />\end{gathered} \]](/tex-image/8671faf901ac8b25a8461e0e1513829c.png) ![TEX: \[\begin{gathered}<br /> u = \sin x \hfill \\<br /> \sin u + \sin (u){u^2} + u\sqrt {1 - {{\sin }^2}(u)} = - 3u \hfill \\<br /> u\sqrt {1 - {{\sin }^2}(u)} = - 3u - \sin u - \sin (u){u^2} \hfill \\ <br />\end{gathered} \]](/tex-image/ad28002618fe07ddcac88d27c8f65764.png) ![TEX: \[\begin{gathered}<br /> \sin (u)(1 - {u^2}) = - 3u + u\sqrt {1 - {{\sin }^2}(u)} \hfill \\<br /> \sin (u)(1 - {u^2}) = - 3u(1 - \sqrt {1 - {{\sin }^2}(u)} ) \hfill \\<br /> {\text{Arreglado error signo al derivar cos en 2da linea y el menos en 4ta linea}} \hfill \\ <br />\end{gathered} \]](/tex-image/3a7b8258a25365f5d0da1887326feecd.png) ¿porque derivas al inicio? Ya que nadie te va a explicar porque no resulta (y si lo intentan hacer quiza no entiendas) te doy un ejemplo. Cos(x)=x Derivando, según tu Sin(x)=-1 Con eso, según tu X=(4n+3)pi/2 Pero todos esos valores te dan 0 en el coseno por lo que Cos(x) es siempre distinto de x. |
|
|
|
 Jun 15 2018, 11:41 PM Jun 15 2018, 11:41 PM
Publicado:
#5
|
|
|
Maestro Matemático Grupo: Usuario FMAT Mensajes: 128 Registrado: 27-November 15 Miembro Nº: 142.558 |

Mensaje modificado por hermite el Jun 15 2018, 11:42 PM |
|
|
|
 Jun 16 2018, 02:27 AM Jun 16 2018, 02:27 AM
Publicado:
#6
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 524 Registrado: 2-October 13 Miembro Nº: 122.939 Nacionalidad:  Sexo:  |
Quizas estoy complejizandolo, no creo :/ Le doy un poco de avance ![TEX: \[\begin{gathered}<br /> 2 + \cos (\sin x)\cos x = 3\cos x \hfill \\<br /> (\cos (\sin x))'\cos x + \cos (\sin x)\sin x = - 3senx \hfill \\<br /> - \sin (\sin x){\cos ^2}x + \cos (\sin x)\sin x = - 3senx \hfill \\<br /> - \sin (\sin x)(1 - {\sin ^2}x) + \cos (\sin x)\sin x = - 3senx \hfill \\<br /> \sin (\sin x) + \sin (\sin x)({\sin ^2}x) + \sin x\cos (\sin x) = - 3\sin x \hfill \\<br /> \sin (\sin x) + \sin (\sin x)({\sin ^2}x) + \sin x(\sqrt {1 - {{\sin }^2}(\sin x} ) = - 3\sin x \hfill \\ <br />\end{gathered} \]](/tex-image/8671faf901ac8b25a8461e0e1513829c.png) ![TEX: \[\begin{gathered}<br /> u = \sin x \hfill \\<br /> \sin u + \sin (u){u^2} + u\sqrt {1 - {{\sin }^2}(u)} = - 3u \hfill \\<br /> u\sqrt {1 - {{\sin }^2}(u)} = - 3u - \sin u - \sin (u){u^2} \hfill \\ <br />\end{gathered} \]](/tex-image/ad28002618fe07ddcac88d27c8f65764.png) ![TEX: \[\begin{gathered}<br /> \sin (u)(1 - {u^2}) = - 3u + u\sqrt {1 - {{\sin }^2}(u)} \hfill \\<br /> \sin (u)(1 - {u^2}) = - 3u(1 - \sqrt {1 - {{\sin }^2}(u)} ) \hfill \\<br /> {\text{Arreglado error signo al derivar cos en 2da linea y el menos en 4ta linea}} \hfill \\ <br />\end{gathered} \]](/tex-image/3a7b8258a25365f5d0da1887326feecd.png) loco ya te dijeron hace meses que derivar una ecuación no la resuelve, y lo sigues haciendo indiscriminadamente en cada problema que no sabes resolver, al menos demuestra un poco de progreso, que vas aprendiendo o que al menos lees el feedback que te da la gente con sus respuestas en el foro saludos |
|
|
|
 Jun 16 2018, 02:45 AM Jun 16 2018, 02:45 AM
Publicado:
#7
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 947 Registrado: 28-September 07 Desde: Santiago Miembro Nº: 10.639 Nacionalidad:  Universidad:  Sexo:  |
loco ya te dijeron hace meses que derivar una ecuación no la resuelve, y lo sigues haciendo indiscriminadamente en cada problema que no sabes resolver, al menos demuestra un poco de progreso, que vas aprendiendo o que al menos lees el feedback que te da la gente con sus respuestas en el foro saludos Resuelva 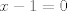 Solución: derivando, 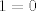 |
|
|
|
 Jun 16 2018, 01:07 PM Jun 16 2018, 01:07 PM
Publicado:
#8
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.875 Registrado: 27-December 07 Desde: ∂Ω©ȹʕѺϧگἐᾋ1©Ӹ█₯►☻X TH.....I FORGOR Miembro Nº: 14.122 Nacionalidad:  Universidad:  Sexo:  |
ahora entiendo.
Lo que sucede es que legi cree que resolver f(x)=g(x), implica que tambien f'(x)=g'(x) lo cual esta maaaaaaal: de partida. decir f(x)=g(x) no se puede inferir nada si no hay un contexto. Por ejemplo. es muy distinto decir f(x)=g(x) para ALGUN x, que f(x)=g(x) para TODO x. solo es posible decir (creo, bajo ciertas condiciones) f'(x)=g'(x) en el segundo caso. en el primero no. ya dieron algunos ejemplos de eso. Deberia el Legi darse la cacha' con eso. si es que puede. Saludos Claudio. -------------------- Claudio Henriquez Tapia Ingeniero Civil Matemático UTFSM y Prof. DMAT UTFSM Candidato a Doctor en Estadística UC. Campus San Joaquin Si todo sale bien, estaría defendiendo en Julio 2024. [indent] everywhere at the end of FMAT fmat needs .... To Survive... 3ch03s facts: Frases para el bronce by 3ch03s: Fmat dejame subir mas citas! TB-3030303 que es YTP-Tennis: |
|
|
|
 Jun 16 2018, 09:43 PM Jun 16 2018, 09:43 PM
Publicado:
#9
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 524 Registrado: 2-October 13 Miembro Nº: 122.939 Nacionalidad:  Sexo:  |
ahora entiendo. Lo que sucede es que legi cree que resolver f(x)=g(x), implica que tambien f'(x)=g'(x) lo cual esta maaaaaaal: de partida. decir f(x)=g(x) no se puede inferir nada si no hay un contexto. Por ejemplo. es muy distinto decir f(x)=g(x) para ALGUN x, que f(x)=g(x) para TODO x. solo es posible decir (creo, bajo ciertas condiciones) f'(x)=g'(x) en el segundo caso. en el primero no. ya dieron algunos ejemplos de eso. Deberia el Legi darse la cacha' con eso. si es que puede. Saludos Claudio. basta con que haya igualdad en un conjunto de puntos que se esten acumulando en otro punto para poder definir la derivada cuyas propiedades conocemos si el conjunto es discreto o hay puntos que no son de acumulación vamos a quedar tan en ridículo como legi al hacer eso |
|
|
|
 Jun 22 2018, 01:19 AM Jun 22 2018, 01:19 AM
Publicado:
#10
|
|
|
Matemático Grupo: Usuario FMAT Mensajes: 49 Registrado: 26-May 18 Miembro Nº: 157.415 Nacionalidad:  Sexo:  |
-------------------- Estudiante de Ingeniería
|
|
|
|
  |
2 usuario(s) está(n) leyendo esta discusión (2 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 23rd November 2024 - 06:06 PM |












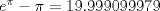


![TEX: \[x' = 0\]](/tex-image/2f831e084ec7942a789831021502f9d5.png)