Identificarse Registrarse

Psu
Enseñanza Básica
Enseñanza Media
Universidad
Olimpiadas
Comunidad



 
 Reply to this topicStart new topic
> Propuesto normal
Uchiha Itachi
mensaje Jan 14 2010, 11:05 PM
Publicado: #1


Staff FMAT
Ícono de Grupo

Grupo: Super Moderador
Mensajes: 4.857
Registrado: 2-January 08
Miembro Nº: 14.268
Nacionalidad:
Colegio/Liceo: The Garden School
Universidad: Universidad de Chile-FCFM
Sexo:



TEX: % MathType!MTEF!2!1!+-<br />% feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaae4uaiaabM<br />% gacaqGGaGaae4raiaabccacaqGLbGaae4CaiaabccacaqG1bGaaeOB<br />% aiaabccacaqGNbGaaeOCaiaabwhacaqGWbGaae4BaiaabccacaqGHb<br />% GaaeOyaiaabwgacaqGSbGaaeyAaiaabggacaqGUbGaae4BaiaabYca<br />% caqGGaGaaeyzaiaab6gacaqG0bGaae4Baiaab6gacaqGJbGaaeyzai<br />% aabohacaqGGaGaaeizaiaabwgacaqGTbGaaeyDaiaabwgacaqGZbGa<br />% aeiDaiaabkhacaqGLbGaaeiiaiaabghacaqG1bGaaeyzaiaabccaca<br />% qG0bGaae4BaiaabsgacaqGVbGaaeiiaiaabohacaqG1bGaaeOyaiaa<br />% bEgacaqGYbGaaeyDaiaabchacaqGVbGaaeiiaiaabsgacaqGLbGaae<br />% iiaiaabEeacaqGGaGaaeyzaiaabohacaqGGaGaaeOBaiaab+gacaqG<br />% YbGaaeyBaiaabggacaqGSbGaaeOlaaaa!7AB0!<br />\[<br />{\text{Si G es un grupo abeliano}}{\text{, entonces demuestre que todo subgrupo de G es normal}}{\text{.}}<br />\]<br />


--------------------
Candidato a doctor en Cs. De la ingeniería mención modelamiento matemático, DIM. Universidad de Chile

Magíster en ciencias mención matemática,
Profesor de estado en matemáticas y computación,
Licenciado en educación matemáticas y computación,
USACH
Go to the top of the page
 
+Quote Post
coquitao
mensaje Jan 14 2010, 11:22 PM
Publicado: #2


Dios Matemático Supremo
Ícono de Grupo

Grupo: Super Moderador
Mensajes: 2.065
Registrado: 25-May 08
Desde: Pelotillehue
Miembro Nº: 24.463
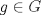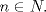Trivial. Si N es un subgrupo de G entonces TEX: $gng^{-1} = e \in N$ para cada TEX: $g \in G$ y TEX: $n \in N.$ QED.

Es mucho más interesante el análisis de la implicación recíproca:

http://www.fmat.cl/index.php?showtopic=51156


--------------------
"Please forget everything you have learned in school; for you haven't learned it... Please keep in mind at all times the corresponding portions of your school curriculum; for you haven't actually forgotten them." -- E. Landau
Go to the top of the page
 
+Quote Post
Edwin Wilfredo V...
mensaje Apr 26 2014, 02:34 PM
Publicado: #3


Principiante Matemático
Ícono de Grupo

Grupo: Usuario FMAT
Mensajes: 3
Registrado: 26-April 14
Miembro Nº: 128.969
Nacionalidad:
Sexo:



CITA(Uchiha Itachi @ Jan 14 2010, 11:05 PM) *
TEX: % MathType!MTEF!2!1!+-<br />% feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaae4uaiaabM<br />% gacaqGGaGaae4raiaabccacaqGLbGaae4CaiaabccacaqG1bGaaeOB<br />% aiaabccacaqGNbGaaeOCaiaabwhacaqGWbGaae4BaiaabccacaqGHb<br />% GaaeOyaiaabwgacaqGSbGaaeyAaiaabggacaqGUbGaae4BaiaabYca<br />% caqGGaGaaeyzaiaab6gacaqG0bGaae4Baiaab6gacaqGJbGaaeyzai<br />% aabohacaqGGaGaaeizaiaabwgacaqGTbGaaeyDaiaabwgacaqGZbGa<br />% aeiDaiaabkhacaqGLbGaaeiiaiaabghacaqG1bGaaeyzaiaabccaca<br />% qG0bGaae4BaiaabsgacaqGVbGaaeiiaiaabohacaqG1bGaaeOyaiaa<br />% bEgacaqGYbGaaeyDaiaabchacaqGVbGaaeiiaiaabsgacaqGLbGaae<br />% iiaiaabEeacaqGGaGaaeyzaiaabohacaqGGaGaaeOBaiaab+gacaqG<br />% YbGaaeyBaiaabggacaqGSbGaaeOlaaaa!7AB0!<br />\[<br />{\text{Si G es un grupo abeliano}}{\text{, entonces demuestre que todo subgrupo de G es normal}}{\text{.}}<br />\]<br />


Archivo(s) Adjunto(s)
Archivo Adjunto  sshot_1.png ( 24.83k ) Número de descargas:  0
 
Go to the top of the page
 
+Quote Post
 

Reply to this topicStart new topic
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):

 

Versión Lo-Fi Fecha y Hora actual: 3rd April 2025 - 11:47 PM
Powered By IP.Board 2.2.1 © 2007  IPS, Inc.