|
|
|
|
|
|
|
  |
 Jan 14 2010, 01:28 PM Jan 14 2010, 01:28 PM
Publicado:
#1
|
|
 Dios Matemático Supremo Grupo: Team Ensayos FMAT Mensajes: 513 Registrado: 25-April 08 Desde: CSMC Miembro Nº: 21.189 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Se tiene el siguiente orden de circunferencias tal que comenzamos con una de radio
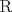 , la siguiente se fija tal que es tangente y pasa por el centro de esta, hacemos esto varias veces intercambiando de lado cada ves. Encontrar a que distancia se halla el centro de la n-sima circunferencia en relacion al punto azul, que es el primer punto de tangencia. Que pasa si , la siguiente se fija tal que es tangente y pasa por el centro de esta, hacemos esto varias veces intercambiando de lado cada ves. Encontrar a que distancia se halla el centro de la n-sima circunferencia en relacion al punto azul, que es el primer punto de tangencia. Que pasa si 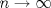 ??? ??? circulos.JPG ( 13.46k )
Número de descargas: 0
circulos.JPG ( 13.46k )
Número de descargas: 0Editado. Mensaje modificado por Nabodorbuco el Jan 15 2010, 07:49 AM -------------------- FunGeometry
SIEMPRE CON LAS MEJORES INTENCIONES DE AYUDAR. ATTE. NABODORBUCO EL TERCER OJO GoGeometry LA IDEA ES QUE NO ESPERES QUE FMAT RESUELVA TUS TAREAS, ESCRIBE SIEMPRE CUALES SON TUS INQUIETUDES |
|
|
|
 Jan 14 2010, 02:24 PM Jan 14 2010, 02:24 PM
Publicado:
#2
|
|
 Dios Matemático Supremo Grupo: Team Ensayos FMAT Mensajes: 1.294 Registrado: 16-March 09 Desde: ancud Miembro Nº: 45.100 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
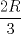 ?? ??si es asi te planteo mi solucion --------------------   Estudiante de 4° año ing civil mec utfsm |
|
|
|
 Jan 14 2010, 03:20 PM Jan 14 2010, 03:20 PM
Publicado:
#3
|
|
 Dios Matemático Supremo Grupo: Team Ensayos FMAT Mensajes: 1.559 Registrado: 18-November 07 Miembro Nº: 12.754 Nacionalidad:  Sexo:  |
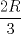 ?? ??si es asi te planteo mi solucion es k es de la enesima po. tienes q ubscar una forma general se me ocurre como haerla, cuando deje de chatear la hago XD saludos -------------------- Empezando con Desigualdades? Encuentra aquí problemas resueltos
|
|
|
|
 Jan 14 2010, 05:22 PM Jan 14 2010, 05:22 PM
Publicado:
#4
|
|
 Dios Matemático Supremo Grupo: Team Ensayos FMAT Mensajes: 513 Registrado: 25-April 08 Desde: CSMC Miembro Nº: 21.189 Nacionalidad:  Colegio/Liceo:  Sexo:  |
-------------------- FunGeometry
SIEMPRE CON LAS MEJORES INTENCIONES DE AYUDAR. ATTE. NABODORBUCO EL TERCER OJO GoGeometry LA IDEA ES QUE NO ESPERES QUE FMAT RESUELVA TUS TAREAS, ESCRIBE SIEMPRE CUALES SON TUS INQUIETUDES |
|
|
|
 Jan 14 2010, 07:55 PM Jan 14 2010, 07:55 PM
Publicado:
#5
|
|
 Dios Matemático Supremo Grupo: Team Ensayos FMAT Mensajes: 1.559 Registrado: 18-November 07 Miembro Nº: 12.754 Nacionalidad:  Sexo:  |
EDIT: Discúlpnenme, ahora, meses despues releyendo el tema, caché que en el enunciado salía "cuando n tiende a infinito", perdón por haber hecho el off topic con el "no veo el n en tu expresión" xD
Saludos! Mensaje modificado por Hamon el Jun 28 2010, 02:09 AM -------------------- Empezando con Desigualdades? Encuentra aquí problemas resueltos
|
|
|
|
 Jan 14 2010, 09:11 PM Jan 14 2010, 09:11 PM
Publicado:
#6
|
|
 Dios Matemático Supremo Grupo: Team Ensayos FMAT Mensajes: 1.294 Registrado: 16-March 09 Desde: ancud Miembro Nº: 45.100 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
bueno, jugando un poko con el dibujito podemos, primeramente, darnos cuenta que los radios de las circunferencias que se van formando cumplen con la siguiente formula :
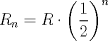 Luego al sumar los respectivos radios para encontrar la distancia 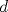 nos encontramos con la sig particularidad: nos encontramos con la sig particularidad: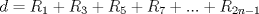 por lo tanto el problema se limita a calcular la sumatoria de todos estos 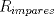 desde el uno hasta el infinito entonces: desde el uno hasta el infinito entonces: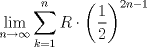 y eso resolviendo me dio 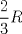 srry por lo breve pero entenderas que eran muchas fraciones XD y me dio mucha flojera hacerlas ademas de que voi viajando mas incomodo bueno ojala te bien saludos --------------------   Estudiante de 4° año ing civil mec utfsm |
|
|
|
 Jan 14 2010, 10:01 PM Jan 14 2010, 10:01 PM
Publicado:
#7
|
|
|
Dios Matemático Supremo Grupo: Baneado Mensajes: 3.360 Registrado: 11-March 08 Miembro Nº: 16.617 |
por que aplicaste limite? no deberia ser
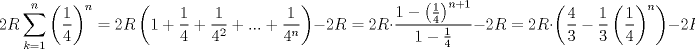 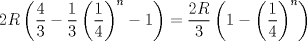
Mensaje modificado por xdanielx el Jan 14 2010, 10:09 PM |
|
|
|
 Jan 14 2010, 10:07 PM Jan 14 2010, 10:07 PM
Publicado:
#8
|
|
 Dios Matemático Supremo Grupo: Team Ensayos FMAT Mensajes: 1.294 Registrado: 16-March 09 Desde: ancud Miembro Nº: 45.100 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
por que aplicaste limite? no deberia ser 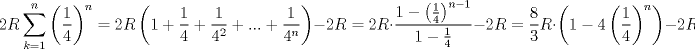 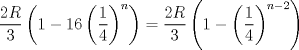 mmm pero se supone q tenemos q encontrar la distancia entre el centro e la n-esima circunferencia y el punto de tangencia azul. y supuse que tendriamos que encontrar en que numero converge, por lo cual aplike limite saludos, corrijame si la vendii xd --------------------   Estudiante de 4° año ing civil mec utfsm |
|
|
|
 Jan 15 2010, 07:48 AM Jan 15 2010, 07:48 AM
Publicado:
#9
|
|
 Dios Matemático Supremo Grupo: Team Ensayos FMAT Mensajes: 513 Registrado: 25-April 08 Desde: CSMC Miembro Nº: 21.189 Nacionalidad:  Colegio/Liceo:  Sexo:  |
La respuesta de xdanielx es correcta, la de felipe martinez es correcta solo si n tiende a infinito. Ahora cuando pense el problema lo resolvi con n tendiendo a infinito, por lo cual claramente la respuesta que esperaba era
 . De todas maneras estas dos respuestas son bastante buenas y dejan en claro las dos cosas que sucedian aqui, por lo cual creo que podemos proceder a que lo envien a resueltos. . De todas maneras estas dos respuestas son bastante buenas y dejan en claro las dos cosas que sucedian aqui, por lo cual creo que podemos proceder a que lo envien a resueltos. -------------------- FunGeometry
SIEMPRE CON LAS MEJORES INTENCIONES DE AYUDAR. ATTE. NABODORBUCO EL TERCER OJO GoGeometry LA IDEA ES QUE NO ESPERES QUE FMAT RESUELVA TUS TAREAS, ESCRIBE SIEMPRE CUALES SON TUS INQUIETUDES |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 8th July 2025 - 01:31 AM |








![TEX: $\sqrt[3]{\dfrac{1}{\cos\left(\frac{\pi}{7}\right)}}-\sqrt[3]{\dfrac{1}{\cos\left(\frac{2\pi}{7}\right)}}+\sqrt[3]{\dfrac{1}{\cos\left(\frac{3\pi}{7}\right)}}=\sqrt[3]{6\sqrt[3]{7}-8}$](./tex/c5b49cf6584e89b12a82db6b29f2cd73.png)



