quieres profundizar - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Programa de Enseñanza Media > 4º Medio > Contenidos 4º Medio

2 Páginas:

1 2 >

Reply to this topic

Start new topic

quieres profundizar, Ecuaciones cubicas y cuarticas?

xdanielx Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 12 2010, 08:39 PM Publicado: #1
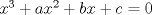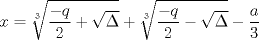Dios Matemático Supremo Grupo: Baneado Mensajes: 3.360 Registrado: 11-March 08 Miembro Nº: 16.617	Conozco dos formas para las cubicas que son mas menos similares, la primera La ecuacion de la forma $TEX: $x^3 + ax^2 + bx + c = 0$$ (1) tiene solucion $TEX: $$<br />x = \root 3 \of {\frac{{ - q}}<br />{2} + \sqrt \Delta } + \root 3 \of {\frac{{ - q}}<br />{2} - \sqrt \Delta } - \frac{a}<br />{3}<br />$$$ donde $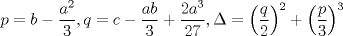TEX: $$<br />p = b - \frac{{a^2 }}<br />{3},q = c - \frac{{ab}}<br />{3} + \frac{{2a^3 }}<br />{{27}},\Delta = \left( {\frac{q}<br />{2}} \right)^2 + \left( {\frac{p}<br />{3}} \right)^3 <br />$$$ la raız cuadrada de Δ se escoge arbitrariamente y, fijada esta, las raıces cubicas u y v se escogen de modo que 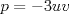$TEX: $$p = -3uv$$$ (es decir, se escoge una arbitrariamente y la otra se calcula mediante esta relacion). Las demostraciones las realizare a medida que vaya postiando, no ando con mucho tiempo debido a que todavia no tomo los ramos :/ Teorema: Consideremos una ecuacion (1) con coeficientes reales. Entonces: 1. Si Δ = 0 todas sus raıces son reales, y al menos dos de ellas son iguales. 2. Si Δ > 0 la ecuacion tiene una raız real y dos raıces imaginarias. 3. Si Δ < 0 la ecuacion tiene tres raıces reales simples. Teorema: Si Δ = 0 hay dos posibilidades: 1. Si p = q = 0, entonces la ecuacion tiene una raız triple x = −a/3. 2. Si pq 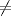$TEX: $ \ne$$ 0, entonces la ecuacion tiene una raız doble y una raız simple, dadas respectivamente por 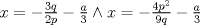$TEX: $x = - \frac{{3q}}{{2p}} - \frac{a}{3} \wedge x = - \frac{{4p^2 }}{{9q}} - \frac{a}{3}$$ Teorema: Si Δ > 0, una raız real viene dada por 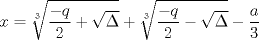$TEX: $$<br />x = \root 3 \of {\frac{{ - q}}<br />{2} + \sqrt \Delta } + \root 3 \of {\frac{{ - q}}<br />{2} - \sqrt \Delta } - \frac{a}<br />{3}<br />$$$ donde las raices cubicas u y v son reales. 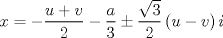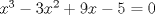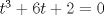Las otras dos raices son imaginarias y vienen dadas por: $TEX: $$<br />x = - \frac{{u + v}}<br />{2} - \frac{a}<br />{3} \pm \frac{{\sqrt 3 }}<br />{2}\left( {u - v} \right)i<br />$$$ veamos un ejemplo aplicando lo aprendido resolver la cubica $TEX: $x^3 - 3x^2 + 9x - 5 = 0$$ Hagamos $TEX: $x = t + 1$$ y nuestra ecuacion se transforma en $TEX: $t^3 + 6t + 2 = 0$$ analizamos 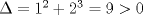$TEX: $\Delta = 1^2 + 2^3 = 9 > 0$$ Entonces la raiz real es $TEX: $x = \root 3 \of { - 1 + \sqrt 9 } + \root 3 \of { - 1 - \sqrt 9 } + 1 = \root 3 \of 2 - \root 3 \of { 4} + 1$$ y las dos imaginarias 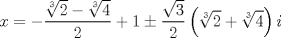$TEX: $$<br />x = - \frac{{\root 3 \of 2 - \root 3 \of 4 }}<br />{2} + 1 \pm \frac{{\sqrt 3 }}<br />{2}\left( {\root 3 \of 2 + \root 3 \of 4 } \right)i<br />$$$ ahora subiendo un poquito el nivel, que pasa con la ecuacion 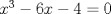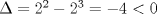$TEX: $x^3 - 6x - 4 =0$$ $TEX: $\Delta = 2^2 - 2^3 = - 4 < 0$$ es decir ha de tener tres raices reales, sin embargo si aplicamos cardano obtenemos una expresion de la forma $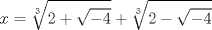TEX: $$<br />x = \root 3 \of {2 + \sqrt { - 4} } + \root 3 \of {2 - \sqrt { - 4} } <br />$$$ Cardano no supo que hacer con este tipo de expresiones. Fue Bombelli el primero que calculo una raız cubica compleja (sin saber muy bien lo que hacıa) similar a estas que nos acabamos de encontrar. 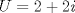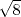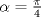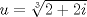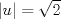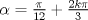En nuestro caso, si llamamos $TEX: $U = 2 +2i$$ tenemos que el modulo de U es $TEX: $\sqrt 8 $$ y su argumento $TEX: $\alpha = \frac{\pi }{4}$$ , luego las raices cubicas $TEX: ${u = \root 3 \of {2 + 2i} }$$ son los numeros complejos de modulo $TEX: ${\left\| u \right\| = \sqrt 2 }$$ y argumento $TEX: $\alpha = \frac{\pi }{{12}} + \frac{{2k\pi }}{3}$$ para k = 0,1,2 esw decir: 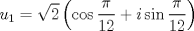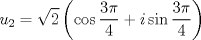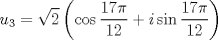$TEX: $$<br />u_1 = \sqrt 2 \left( {\cos \frac{\pi }<br />{{12}} + i\sin \frac{\pi }<br />{{12}}} \right)<br />$$$ $TEX: $$<br />u_2 = \sqrt 2 \left( {\cos \frac{{3\pi }}<br />{4} + i\sin \frac{{3\pi }}<br />{4}} \right)<br />$$$ $TEX: $$<br />u_3 = \sqrt 2 \left( {\cos \frac{{17\pi }}<br />{{12}} + i\sin \frac{{17\pi }}<br />{{12}}} \right)<br />$$$ centremonos en la segunda que es la mas facil de las tres 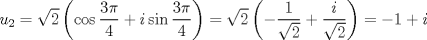$TEX: $$<br />u_2 = \sqrt 2 \left( {\cos \frac{{3\pi }}<br />{4} + i\sin \frac{{3\pi }}<br />{4}} \right) = \sqrt 2 \left( { - \frac{1}<br />{{\sqrt 2 }} + \frac{i}<br />{{\sqrt 2 }}} \right) = - 1 + i<br />$$$ el valor correspondiente a 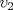$TEX: $v_2$$ se calcula mediante la relacion expuesta al principio $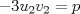TEX: $ - 3u_2 v_2 = p$$ de modo que $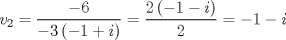TEX: $$<br />v_2 = \frac{{ - 6}}<br />{{ - 3\left( { - 1 + i} \right)}} = \frac{{2\left( { - 1 - i} \right)}}<br />{2} = - 1 - i<br />$$$ (Luego veremos que este calculo no era necesario, porque 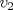$TEX: $v_2$$ teni que ser el conjugado de $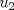TEX: $u_2$$ , precisamente porque la raiz $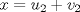TEX: $x = u_2 + v_2$$ ha de ser real.) En total, vemos que una raiz de la ecuacion es $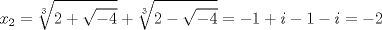TEX: $$<br />x_2 = \root 3 \of {2 + \sqrt { - 4} } + \root 3 \of {2 - \sqrt { - 4} } = - 1 + i - 1 - i = - 2<br />$$$ pero como el grado de la ecuacion es 3 deben existir 3 raices para nuestra ecuacion, las otras raices pueden calcularse del mismo modo, pero, una vez tenemos una de ellas, es mas facil dividir 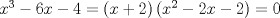$TEX: $x^3 - 6x - 4 = \left( {x + 2} \right)\left( {x^2 - 2x - 2} \right) = 0$$ , con lo que las otras dos raices resultan ser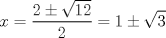 $TEX: $$<br />x = \frac{{2 \pm \sqrt {12} }}<br />{2} = 1 \pm \sqrt 3 <br />$$$ Teorema: Si Δ > 0 la ecuacion tiene tres raices reales simples, que vienen dadas por 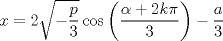$TEX: $$<br />x = 2\sqrt { - \frac{p}<br />{3}} \cos \left( {\frac{{\alpha + 2k\pi }}<br />{3}} \right) - \frac{a}<br />{3}<br />$$$ donde k = 0,1,2 y el angulo 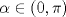$TEX: ${\alpha \in \left( {0,\pi } \right)}$$ segunda parte toda ecuacion de la forma 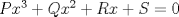$TEX: $Px^3 + Qx^2 + Rx + S = 0$$ (1) se puede llevar a $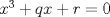TEX: $x^3 + qx + r = 0$$ (2) como? 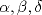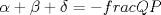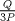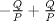aqui vamos, sean $TEX: $\alpha ,\beta ,\delta $$ las raices, entonces se verifica $TEX: $\alpha + \beta + \delta = - frac{Q}{P}$$ , entonces si sumamos a cada una de las raices $TEX: $\frac{Q}{{3P}}$$ en la ecuacion transformada la suma de las raices sera $TEX: $ - \frac{Q}{P} + \frac{Q}{P}$$ esw decir el segundo termino se hara cero. 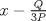entonces basta reemplazar x por $TEX: $x - \frac{Q}{{3P}}$$ haga la prueba para 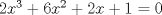$TEX: $2x^3 + 6x^2 + 2x + 1 = 0$$ siguiendo con el tema, como sabemos que toda ecuacion de la forma (1) se puede llevar a la forma (2) aca va lo bello realizado por Scipio Ferreo pero sin embargo Cardano la publico primero. 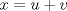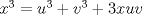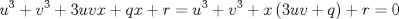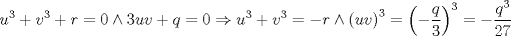hagamos $TEX: $x = u + v$$ entonces $TEX: $x^3 = u^3 + v^3 +3xuv$$ reemplazandolo en (2) $TEX: $$<br />u^3 + v^3 + 3uvx + qx + r = u^3 + v^3 + x\left( {3uv + q} \right) + r = 0<br />$$$ de aqui $TEX: $$<br />u^3 + v^3 + r = 0 \wedge 3uv + q = 0 \Rightarrow u^3 + v^3 = - r \wedge \left( {uv} \right)^3 = \left( { - \frac{q}<br />{3}} \right)^3 = - \frac{{q^3 }}<br />{{27}}<br />$$$ ahora recordemos que 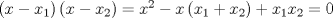$TEX: $\left( {x - x_1 } \right)\left( {x - x_2 } \right) = x^2 - x\left( {x_1 + x_2 } \right) + x_1 x_2 = 0$$ donde en nuestro caso las raices son $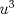TEX: $u^3$$ y $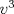TEX: $ v^3$$ $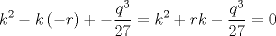TEX: $$<br />k^2 - k\left( { - r} \right) + - \frac{{q^3 }}<br />{{27}} = k^2 + rk - \frac{{q^3 }}<br />{{27}} = 0<br />$$$ $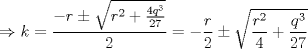TEX: $$<br /> \Rightarrow k = \frac{{ - r \pm \sqrt {r^2 + \frac{{4q^3 }}<br />{{27}}} }}<br />{2} = - \frac{r}<br />{2} \pm \sqrt {\frac{{r^2 }}<br />{4} + \frac{{q^3 }}<br />{{27}}} <br />$$$ entonces 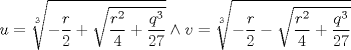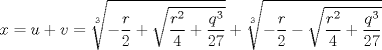$TEX: $$<br />u = \root 3 \of { - \frac{r}<br />{2} + \sqrt {\frac{{r^2 }}<br />{4} + \frac{{q^3 }}<br />{{27}}} } \wedge v = \root 3 \of { - \frac{r}<br />{2} - \sqrt {\frac{{r^2 }}<br />{4} + \frac{{q^3 }}<br />{{27}}} } <br />$$$ $TEX: $$<br />x = u + v = \root 3 \of { - \frac{r}<br />{2} + \sqrt {\frac{{r^2 }}<br />{4} + \frac{{q^3 }}<br />{{27}}} } + \root 3 \of { - \frac{r}<br />{2} - \sqrt {\frac{{r^2 }}<br />{4} + \frac{{q^3 }}<br />{{27}}} } <br />$$$ que es nuestra primera solucion las otras dos se obtienen mediante 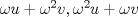$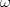TEX: $\omega u + \omega ^2 v,\omega ^2 u + \omega v$$ donde $TEX: $\omega $$ y $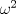TEX: $\omega ^2 $$ son las raices cubicas de la unidad (nacen de la ecuacion $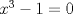TEX: $x^3 - 1 = 0$$ ) o mejor aun 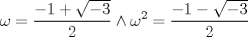$TEX: $$<br />\omega = \frac{{ - 1 + \sqrt { - 3} }}<br />{2} \wedge \omega ^2 = \frac{{ - 1 - \sqrt { - 3} }}<br />{2}<br />$$$ es su conjugado Mensaje modificado por xdanielx el Jan 12 2010, 09:42 PM

teeebo Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 12 2010, 08:59 PM Publicado: #2
Matemático Grupo: Usuario FMAT Mensajes: 69 Registrado: 12-October 09 Desde: Pichilemu, Capital del Surf 8) Miembro Nº: 60.193 Nacionalidad: Universidad: Sexo:	Igual se ve medio cabezón,pensar qe nunca me lo pasaron :S -------------------- POR UN NUEVO CHAT MECHÓN 2010

Kaissa Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 12 2010, 09:06 PM Publicado: #3
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad: Colegio/Liceo: Sexo:	xdanielx solito te metiste en las patas de los caballos: ahora lo obvio que yo pediria seria la demo de como llegar a esa formula seria interesante intentar hacer q la comunidad de fmat se internalizara en EL PROCESO de como lograr ver la formula, no solamente sustituir valores -------------------- Este es un extracto de Qué es fmat by Kenshin. La pregunta para ti estimado(a) lector(a) es... ¿Qué haces tu para que ésto se cumpla?

xdanielx Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 12 2010, 09:10 PM Publicado: #4
Dios Matemático Supremo Grupo: Baneado Mensajes: 3.360 Registrado: 11-March 08 Miembro Nº: 16.617	espera lo que viene con las cuarticas Mensaje modificado por xdanielx el Jan 15 2010, 11:28 AM

xdanielx Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 13 2010, 08:36 PM Publicado: #5
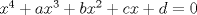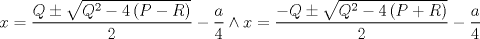Dios Matemático Supremo Grupo: Baneado Mensajes: 3.360 Registrado: 11-March 08 Miembro Nº: 16.617	Ecuaciones Cuarticas (Ferrari) forma 1 La ecuacion de la forma $TEX: $x^4 + ax^3 + bx^2 + cx + d = 0$$ tiene solucion del tipo $TEX: $$<br />x = \frac{{Q \pm \sqrt {Q^2 - 4\left( {P - R} \right)} }}<br />{2} - \frac{a}<br />{4} \wedge x = \frac{{ - Q \pm \sqrt {Q^2 - 4\left( {P + R} \right)} }}<br />{2} - \frac{a}<br />{4}<br />$$$ donde $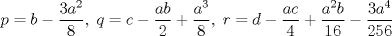TEX: $$<br />p = b - \frac{{3a^2 }}<br />{8},\;q = c - \frac{{ab}}<br />{2} + \frac{{a^3 }}<br />{8},\;r = d - \frac{{ac}}<br />{4} + \frac{{a^2 b}}<br />{{16}} - \frac{{3a^4 }}<br />{{256}}<br />$$$ (1) ahora P es una raiz de la ecuacion 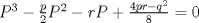$TEX: $P^3 - \frac{p}{2}P^2 - rP + \frac{{4pr - q^2 }}{8} = 0$$ (2) Q y R se determinan mediante las ecuaciones $TEX: $$<br />p = 2P - Q^2 ,\;q = - 2QR,\;r = P^2 - R^2 <br />$$$ (3) mas adeltante veremos que, si $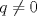TEX: $q \ne 0$$ , la primera ecuacion de (3) es redundante, de modo que, a partir de una solucion P de (2), la tercera ecuacion de (3) nos da un valor para R, necesariamente no nulo, y la segunda ecuacion nos da un valor para Q que necesariamente cumplira la primera ecuacion. 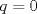Si $TEX: $q = 0$$ el sistema (3) tiene tambien una solucion facil de calcular, pero enseguida veremos que en este caso hay un procedimiento mas rapido para encontrar las raices de la ecuacion. 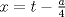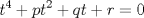En efecto, el cambio de variable $TEX: $x = t - \frac{a}{4}$$ nos lleva a la ecuacion incompleta $TEX: $$<br />t^4 + pt^2 + qt + r = 0<br />$$$ donde p, q, r son los dados por (1). Asi, si q = 0, tenemos lo que se conoce como una ecuacion bicuadrada, cuyas raices cumplen: 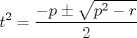$TEX: $$<br />t^2 = \frac{{ - p \pm \sqrt {p^2 - r} }}<br />{2}<br />$$$ luego las cuatro raices de la cuartica son 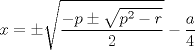$TEX: $$<br />x = \pm \sqrt {\frac{{ - p \pm \sqrt {p^2 - r} }}<br />{2}} - \frac{a}<br />{4}<br />$$$ ejemplo para poner aprueba lo anterior Resolver 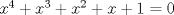$TEX: $x^4 + x^3 + x^2 + x + 1 = 0$$ cuyas raices son las raices quintas no triviales de la unidad. 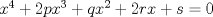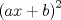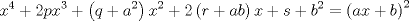forma 2 al mas puro estilo hall and knight - algebra superior, a mi juicio es hermoso y simple Ferrari discipulo de Cardano Sea la ecuacion $TEX: $x^4 + 2px^3 + qx^2 + 2rx + s = 0$$ sumemos a cada miembro $TEX: $\left( {ax + b} \right)^2 $$ siendo determinadas las cantidades a y b de tal manera que hagan que el primer miembro sea un cuadrado perfecto, entonces $TEX: $$<br />x^4 + 2px^3 + \left( {q + a^2 } \right)x^2 + 2\left( {r + ab} \right)x + s + b^2 = \left( {ax + b} \right)^2 <br />$$$ supongamos que el primer miembro de la ecuacion es igual a 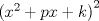$TEX: $\left( {x^2 + px + k} \right)^2 $$ entonces, comparando los coeficientes tenemos: 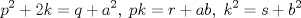$TEX: $$<br />p^2 + 2k = q + a^2 ,\;pk = r + ab,\;k^2 = s + b^2 <br />$$$ eliminando a y b de estas ecuaciones obtenemos 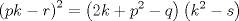$TEX: $$<br />\left( {pk - r} \right)^2 = \left( {2k + p^2 - q} \right)\left( {k^2 - s} \right)<br />$$$ o sea 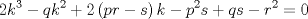$TEX: $$<br />2k^3 - qk^2 + 2\left( {pr - s} \right)k - p^2 s + qs - r^2 = 0<br />$$$ de esta cubica puede hallarse SIEMPRE un valor real de k, luego a y b estan determinados y como 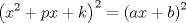$TEX: $$<br />\left( {x^2 + px + k} \right)^2 = \left( {ax + b} \right)^2 <br />$$$ resulta 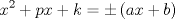$TEX: $$<br />x^2 + px + k = \pm \left( {ax + b} \right)<br />$$$ de aqui estan las cuatro soluciones para la ecuacion cuartica 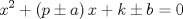$TEX: $$<br />x^2 + \left( {p \pm a} \right)x + k \pm b = 0<br />$$$ forma 3 Por Descartes en el año 1637 supongamos que la ecuacion de cuarto grado es reducida a la forma 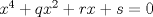$TEX: $x^4 + qx^2 + rx + s = 0$$ y tambien supongamos que 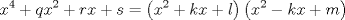$TEX: $$<br />x^4 + qx^2 + rx + s = \left( {x^2 + kx + l} \right)\left( {x^2 - kx + m} \right)<br />$$$ igualdando coeficientes tenemos 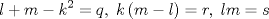$TEX: $$<br />l + m - k^2 = q,\;k\left( {m - l} \right) = r,\;lm = s<br />$$$ de las dos primeras ecuaciones obtenemos 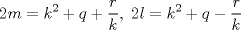$TEX: $$<br />2m = k^2 + q + \frac{r}<br />{k},\;2l = k^2 + q - \frac{r}<br />{k}<br />$$$ sustituyendo en la tercera ecuacion 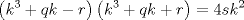$TEX: $$<br />\left( {k^3 + qk - r} \right)\left( {k^3 + qk + r} \right) = 4sk^2 <br />$$$ o sea 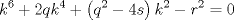$TEX: $$<br />k^6 + 2qk^4 + \left( {q^2 - 4s} \right)k^2 - r^2 = 0<br />$$$ que es una cubica encubierta en 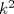$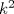TEX: $k^2$$ que tiene siempre una solucion real positiva, luego cuando se conoce $TEX: $k^2$$ se pueden determinar los valores de m y l y la solucion de la ecuacion cuartica se obtiene resolviendo dos cuadraticas que son $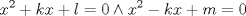TEX: $$<br />{x^2 + kx + l = 0 \wedge x^2 - kx + m = 0}<br />$$$ Ejemplo resolvamos la cuartica 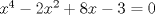$TEX: $x^4 - 2x^2 + 8x - 3 = 0$$ Hagamos 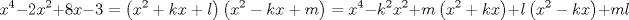$TEX: $$<br />x^4 - 2x^2 + 8x - 3 = \left( {x^2 + kx + l} \right)\left( {x^2 - kx + m} \right) = x^4 - k^2 x^2 + m\left( {x^2 + kx} \right) + l\left( {x^2 - kx} \right) + ml<br />$$$ comparando coeficientes 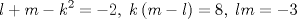$TEX: $$<br />l + m - k^2 = - 2,\;k\left( {m - l} \right) = 8,\;lm = - 3<br />$$$ de este sistema de ecuaciones obtenemos 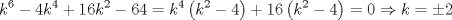$TEX: $\left( {k^3 - 2k + 8} \right)\left( {k^3 - 2k - 8} \right) = - 12k^2 $$ o bien $TEX: $$<br />k^6 - 4k^4 + 16k^2 - 64 = k^4 \left( {k^2 - 4} \right) + 16\left( {k^2 - 4} \right) = 0 \Rightarrow k = \pm 2<br />$$$ que es la solucion real, ahora basta tomar solo una k = 2 reemplazando en las ecuaciones anteriores 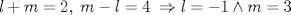$TEX: $l + m = 2,\;m - l = 4\; \Rightarrow l = - 1 \wedge m = 3$$ luego 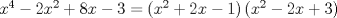$TEX: $x^4 - 2x^2 + 8x - 3 = \left( {x^2 + 2x - 1} \right)\left( {x^2 - 2x + 3} \right)$$ por lo tanto $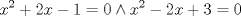TEX: $$<br />{x^2 + 2x - 1 = 0 \wedge x^2 - 2x + 3 = 0}<br />$$$ resolviendo las cuadraticas obtenemos las 4 soluciones de la cuartica Mensaje modificado por xdanielx el Jan 14 2010, 11:10 AM

mikel ramone Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 13 2010, 08:51 PM Publicado: #6
Dios Matemático Grupo: Usuario FMAT Mensajes: 363 Registrado: 27-September 09 Desde: Desde el más arido rock!!! :D Miembro Nº: 59.392 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	excelente aporte siempre es bueno saber mas apenas salga de la U me dedicare a revisar con detencion tu post (Y) arigato!!!! -------------------- Tampoco entendemos si no es. $TEX: $$\underset{\varepsilon \to 0}{\mathop{\lim }}\,\frac{\varepsilon }{\text{ }\varepsilon ^{2}}=\infty$$$ El 98% de los adolescentes han fumado, si eres del dichoso 2% que no lo ha hecho, copia y pega esto en tu firma

xdanielx Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 14 2010, 11:06 AM Publicado: #7
Dios Matemático Supremo Grupo: Baneado Mensajes: 3.360 Registrado: 11-March 08 Miembro Nº: 16.617	Resolver 1) 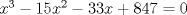$TEX: $x^3 - 15x^2 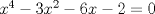- 33x + 847 = 0$$ 2) $TEX: $x^4 - 3x^2 - 6x - 2 = 0$$ a ver como les va aqui hay un link http://deim.urv.cat/~bherrera/cardano.html algo parecido a lo recien visto http://www.gratisweb.com/juanfco20004/cubica.pdf Aca un propuesto aun sin resolver, implica una cubica, quien se anima? http://www.fmat.cl/index.php?showtopic=53889 Mensaje modificado por xdanielx el Jan 14 2010, 09:42 PM

xdanielx Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 21 2010, 12:07 PM Publicado: #8
Dios Matemático Supremo Grupo: Baneado Mensajes: 3.360 Registrado: 11-March 08 Miembro Nº: 16.617	http://www.math.vanderbilt.edu/~schectex/courses/cubic/ les dejo mas informacion Les dejo una ecuacion como ejercicio, tiene dos soluciones una con incognitas auxiliares y otra a lo bruto que arma una cubica 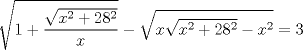$TEX: $$<br />\sqrt {1 + \frac{{\sqrt {x^2 + 28^2 } }}<br />{x}} - \sqrt {x\sqrt {x^2 + 28^2 } - x^2 } = 3<br />$$$ encuentre las raices reales Mensaje modificado por xdanielx el Jan 21 2010, 12:14 PM

Ma.ca Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 24 2011, 06:00 PM Publicado: #9
Principiante Matemático Grupo: Usuario FMAT Mensajes: 4 Registrado: 16-January 11 Miembro Nº: 83.087 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	. -------------------- http://i878.photobucket.com/albums/ab350/sackm/Userbar/UTFSMstubar.png

Ernesto Piwonka Ver Perfil del Miembro Ver los mensajes de este miembro	Apr 21 2013, 08:32 PM Publicado: #10
Dios Matemático Supremo Grupo: Colaborador Gold Mensajes: 874 Registrado: 18-October 07 Desde: The Matrix... Miembro Nº: 11.478 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(Kaissa @ Jan 12 2010, 10:06 PM) xdanielx solito te metiste en las patas de los caballos: ahora lo obvio que yo pediria seria la demo de como llegar a esa formula seria interesante intentar hacer q la comunidad de fmat se internalizara en EL PROCESO de como lograr ver la formula, no solamente sustituir valores Lo publiqué una vez: http://www.fmat.cl/index.php?s=&showto...st&p=438368 -------------------- Saludos, EPC http://epiwonka.blogspot.com

« Posterior · Contenidos 4º Medio · Anterior »

2 Páginas:

1 2 >

Reply to this topic

Start new topic

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 3rd April 2025 - 10:42 AM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.