certamen 2 2009 - Foro fmat.cl

Foro fmat.cl > Programa Enseñanza Universitaria > Comunidades Universitarias > Universidad de Concepción > Introducción al Razonamiento Matemático

2 Páginas:

1 2 >

certamen 2 2009

Opciones

frajavier Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 4 2010, 12:56 AM Publicado: #1
Principiante Matemático Grupo: Usuario FMAT Mensajes: 3 Registrado: 14-August 08 Desde: concepcion Miembro Nº: 32.246 Nacionalidad: Universidad: Sexo:	aqui va el2 Archivo(s) Adjunto(s) exam2_09_.pdf ( 76.31k ) Número de descargas: 293

Kaissa Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 4 2010, 01:38 PM Publicado: #2
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad: Colegio/Liceo: Sexo:	para el problema 4 se vale tomar un cuadradito interior de lado raiz de 2, explicar su no numerabilidad, luego tomar producto cartesiano, y como la circunferencia es mas grande entonces debe tambien ser no numerable? -------------------- Este es un extracto de Qué es fmat by Kenshin. La pregunta para ti estimado(a) lector(a) es... ¿Qué haces tu para que ésto se cumpla?

aleph_omega Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 4 2010, 02:15 PM Publicado: #3
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 560 Registrado: 24-December 09 Miembro Nº: 64.629	No me agrada ese argumento, prefiero mostrar una biyeccion entre la esfera unitaria y la recta real....

felper Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 31 2010, 11:40 AM Publicado: #4
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.767 Registrado: 21-January 08 Desde: Santiago - Ancud Miembro Nº: 14.865 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Pregunta 1: $TEX: $\\${\bf Proposición:} $\mathbb{Q}$ no es completo. $\\$ {\bf Demostración:} $\\$ Considere la sucesión dada por $a_n = \begin{cases} <br /> 1, & \text{ si } n=1 \\<br /> \dfrac{\left[10^n(\sqrt{2}-a_{n-1})\right]}{10^n}+a_{n-1}, & \text{si } n>1 <br />\end{cases} \\$, donde $\left[\quad \right]$ es la función parte entera. $\\$ Podemos ver que esta sucesión de Cauchy converge al número irracional $\sqrt{2}$, el cuál no existe en $\mathbb{Q}$, por lo que el límite de la sucesión no existe. Luego, $\mathbb{Q}$ no es completo. $\Box$$ Pregunta 3: $TEX: $\\$Consideremos la sucesión $\\a_n=\dfrac{n}{n+1}.\\$<br />{\bf Proposición}: La sucesión es monótona creciente. <br />$\\$ {\bf Demostración:} \begin{align} a_n &< a_{n+1} \\ \Leftrightarrow \dfrac{n}{n+1}&<\dfrac{n+1}{n+2} \\ \Leftrightarrow n^2+2n &< n^2+2n +1 \\ \Leftrightarrow 0&<1 \quad \Box \end{align} {\bf Proposición:}La sucesión es acotada. $\\$ {\bf Demostración:}\begin{align}\dfrac{n}{n+1}&< 1 \\ \Leftrightarrow n&<n+1 \\\Leftrightarrow 0&<1 \quad \Box \end{align} Dado que la sucesión es creciente y acotada, podemos asegurar que el límite existe. $\\$Determinemos ahora el límite de la sucesión: $\\ a_n=\dfrac{n}{n+1}=\dfrac{1}{1+\frac{1}{n}}\Rightarrow \displaystyle\lim_{n\to \infty} a_n=1\\$ Con lo que el extremo superior (o supremo) es 1. Podemos ver también que no existe ningún $n$ tal que $a_n=1$, con lo que el máximo de la sucesión no existe. $\\$Ahora, dado que la sucesión es creciente, el menor valor que alcanza (mínimo), así como el ínfimo, está dado por $a_1=\dfrac{1}{2}$.$ Pregunta 4: $TEX: $\\${\bf Proposición:} La circunferencia unitaria $S^1$ no es numerable. $\\${\bf Demostración:} $\\$Consideremos la parametrización de la circunferencia dada por $(x,y)=(\cos(t),\sin(t)),t \in ( 0,2 \pi )$. Podemos ver que esta parametrización, establece una biyección entre la parte superior de la circunferencia ($y\geq0$) y el intervalo $\left[-1,1\right]$, cuya no numerabilidad es una consecuencia inmediata de la no numerabilidad del intervalo $\left[0,1\right]$, cuya prueba es conocida. Con este argumento, hemos mostramos que la parte superior de la circunferencia, no es numerable. El argumento para la parte inferior es totalmente análogo. Luego, como la circunferencia es la unión de dos conjuntos no numerables, es también no numerable. $\Box$$ -------------------- Estudia para superarte a ti mismo, no al resto.

Kaissa Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 31 2010, 11:51 AM Publicado: #5
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad: Colegio/Liceo: Sexo:	$TEX: $ $\\<br />Menos complicaciones para el problema 1: tomamos la secuencia $a_{1}=3$, $a_{2}=3.1$, $a_{3}=3.14$ etc etc convergente a $\pi$ irracional y por arqu\'imedes, de Cauchy.$ -------------------- Este es un extracto de Qué es fmat by Kenshin. La pregunta para ti estimado(a) lector(a) es... ¿Qué haces tu para que ésto se cumpla?

Kaissa Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 31 2010, 12:13 PM Publicado: #6
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad: Colegio/Liceo: Sexo:	$TEX: $ $\\<br />Para el problema 4 tengo algo distinto, aunque debo decir que felper lo hizo de maravilla. He aqu\'i mi estilo:\\<br />$ $\\<br />Trasladamos $S_{1}$ de modo que su centro sea $(0,1)$ y fijemos el punto $Q=(0,2)$.\\<br />Para cada $t\in\mathbb{R}$ trazamos el segmento que une $t$ con $Q$ y marcamos el punto $t_{S}$ en que este segmento corta a $S_{1}$.\\<br />No es nada del otro mundo ver que esta construcci\'on proyecta toda $S_{1}$ sobre $\mathbb{R}$ de manera biyectiva.\\<br />En conclusi\'on tenemos un conjunto biyectivizado sobre un no numerable.$ Mensaje modificado por Kaissa el Jan 31 2010, 12:14 PM -------------------- Este es un extracto de Qué es fmat by Kenshin. La pregunta para ti estimado(a) lector(a) es... ¿Qué haces tu para que ésto se cumpla?

felper Ver Perfil del Miembro Ver los mensajes de este miembro	Feb 7 2010, 02:16 PM Publicado: #7
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.767 Registrado: 21-January 08 Desde: Santiago - Ancud Miembro Nº: 14.865 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	En la 2, ¿qué pasa si $TEX: $a=-(\sqrt{b})^3 \implies \sqrt[3]{a}+\sqrt{b}=0 \notin \mathbb{I}$$ ? o estoy muy perdido? -------------------- Estudia para superarte a ti mismo, no al resto.

Kaissa Ver Perfil del Miembro Ver los mensajes de este miembro	Feb 7 2010, 02:21 PM Publicado: #8
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad: Colegio/Liceo: Sexo:	ambos deben dar positivo y si le pones raiz a b negativo quedamos como chaleco de mono u.u -------------------- Este es un extracto de Qué es fmat by Kenshin. La pregunta para ti estimado(a) lector(a) es... ¿Qué haces tu para que ésto se cumpla?

aleph_omega Ver Perfil del Miembro Ver los mensajes de este miembro	Feb 7 2010, 02:36 PM Publicado: #9
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 560 Registrado: 24-December 09 Miembro Nº: 64.629	CITA(felper @ Jan 31 2010, 12:40 PM) Pregunta 1: $TEX: $\\${\bf Proposición:} $\mathbb{Q}$ no es completo. $\\$ {\bf Demostración:} $\\$ Considere la sucesión dada por $a_n = \begin{cases} <br /> 1, & \text{ si } n=1 \\<br /> \dfrac{\left[10^n(\sqrt{2}-a_{n-1})\right]}{10^n}+a_{n-1}, & \text{si } n>1 <br />\end{cases} \\$, donde $\left[\quad \right]$ es la función parte entera. $\\$ Podemos ver que esta sucesión de Cauchy converge al número irracional $\sqrt{2}$, el cuál no existe en $\mathbb{Q}$, por lo que el límite de la sucesión no existe. Luego, $\mathbb{Q}$ no es completo. $\Box$$ Debes mostrar que la sucesión es efectivamente de cauchy. (Se restan puntos si no lo haces, una vez a mi me restaron la mitad) Además, sería mejor redactar como "esta sucesión no converge en 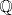$TEX: $\mathbb{Q}$$ " en vez de escribir "...por lo que el límite de la sucesión no existe". Mensaje modificado por aleph_omega el Feb 7 2010, 02:41 PM

felper Ver Perfil del Miembro Ver los mensajes de este miembro	Feb 7 2010, 02:51 PM Publicado: #10
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.767 Registrado: 21-January 08 Desde: Santiago - Ancud Miembro Nº: 14.865 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(aleph_omega @ Feb 7 2010, 04:36 PM) Debes mostrar que la sucesión es efectivamente de cauchy. (Se restan puntos si no lo haces, una vez a mi me restaron la mitad) Además, sería mejor redactar como "esta sucesión no converge en 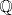$TEX: $\mathbb{Q}$$ " en vez de escribir "...por lo que el límite de la sucesión no existe". Aahaa, la sucesión que expuse fue construida de la misma forma que la de Kaissa, es decir, es sólo una expresión que entrega un decimal más por cada término de la sucesión. La sucesión es de Cauchy por la misma justificación que la de Kaissa, por la propiedad Arquimediana. -------------------- Estudia para superarte a ti mismo, no al resto.

« Posterior · Introducción al Razonamiento Matemático · Anterior »

2 Páginas:

1 2 >

2 usuario(s) está(n) leyendo esta discusión (2 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 23rd November 2024 - 06:08 PM