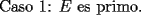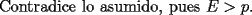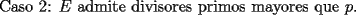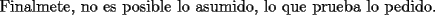|
|
|
|
|
|
|
  |
 Nov 1 2006, 10:31 PM Nov 1 2006, 10:31 PM
Publicado:
#11
|
|
 Matemático Grupo: Usuario FMAT Mensajes: 40 Registrado: 19-July 06 Desde: Conce, Jazz Capitol Miembro Nº: 1.716 Nacionalidad:  Sexo:  |
Creo k te precipitaste un poco,
CITA(Luffy @ Oct 11 2006, 06:12 PM) Suponga que existen finitos primos de la forma 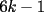 , luego sean , luego sean 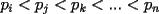 dichos primos. Luego el número dichos primos. Luego el número 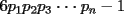 es mayor que es mayor que 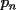 , pero además, ningún primo menor que dicho número lo divide. Por lo tanto es un primo de la forma , pero además, ningún primo menor que dicho número lo divide. Por lo tanto es un primo de la forma 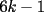 mayor que mayor que 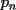 . . 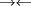  Existen infinitos primos de la forma Existen infinitos primos de la forma 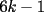 |
|
|
|
  |
2 usuario(s) está(n) leyendo esta discusión (2 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 3rd April 2025 - 09:53 PM |