Tablerito de nxn - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Sector Preparación Olimpiadas > Sector Olímpico > Álgebra > Problemas Resueltos

Reply to this topic

Start new topic

Tablerito de nxn

~Fatal_Collapse~ Ver Perfil del Miembro Ver los mensajes de este miembro	Dec 7 2009, 09:50 AM Publicado: #1
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.564 Registrado: 12-November 07 Desde: La Union, XIV Region de los Rios Miembro Nº: 12.607 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: Considere dos secuencias $x_1, x_2,..., x_n$ y $y_1, y_2,..., y_n$ de reales, donde los $2n$ reales son distintos entre si. Sea $T$ un tablero de $nxn$, y sea $a_{i,j}$ un numero en el casillero ubicado en la i-esima fila y j-esima columna. Sabemos que $a_{i,j}=x_i+y_j$ para todo $i,j$ En cada columna multiplicamos todos los numeros ubicados en dicha columna. Sorprendentemente vemos que todos los productos son iguales a 2009. Demuestre que los productos de los numeros en cada fila es el mismo, y determine los posibles valores de este producto$ Si necesitan hint, pidan nomas, saludos -------------------- Ricardo Vargas Obando Ex-alumno Deutsche Schule La Unión (Generación 2010, de los 150 años). Novato de Licenciatura en Matemática/Estadística, en la Pontificia Universidad Católica de Chile. Grupo de facebook de Novatos Matemática y Estadística PUC 2011 Currículum Olímpico: Medalla de Plata, XIX Olimpiada Nacional de Matemática Nivel Menor (2007) Medalla de Oro, XXI Olimpiada Nacional de Matemática Nivel Mayor (2009) Medalla de Bronce, XXV Olimpiada Iberoamericana de Matemática (2010) Medalla de Oro, XXII Olimpiada Nacional de Matemática Nivel Mayor (2010) "What we learned as children, that one plus one equals two, we know to be false. One plus one equals one. We even have a word when you plus another, equals one. That word is love." "Todos piensan en cambiar el mundo, pero nadie piensa en cambiarse a sí mismo."

xD13G0x Ver Perfil del Miembro Ver los mensajes de este miembro	Dec 12 2009, 05:01 PM Publicado: #2
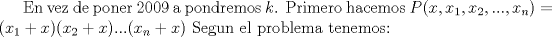Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 532 Registrado: 19-October 08 Desde: Santa Cruz de la Sierra Miembro Nº: 36.531 Nacionalidad: Sexo:	Realmente no soy bueno en algebra, pero creo q este problema me salio $TEX: En vez de poner 2009 a pondremos $k$. Primero hacemos $P(x,x_1,x_2,...,x_n)=(x_1+x)(x_2+x)...(x_n+x)$ Segun el problema tenemos:$ $TEX: $P(y_i)=(x_1+y_i)(x_2+y_i)...(x_n+y_i)=k$ para $i=1,2,...,n$. Ahora hacemos $a_i(x_1,...,x_n)= \sum {x_{j_1}x_{j_2}...x_{j_i}}$ (la suma es tomada sobre todos los subconjuntos de $i$ elementos $\{ j_1,...,j_i \}$ de $\{ 1,2,...,n \}$). Entonces $P(y_i)=y_i^n+a_iy_i^{n-1}+...+a_{n-1}y_i+a_n=k$ para $i=1,2,...,n$ Entonces $y_1,y_2,...,y_n$ son las raices del polinomio $P(x,x_1,x_2,...,x_n)-k$ en $x$ de grado $n$. Definimos $b_i(y_1,...,y_n)= \sum {y_{j_1}y_{j_2}...y_{j_i}}$ (la suma es tomada sobre todos los subconjuntos de $i$ elementos $\{ j_1,...,j_i \}$ de $\{ 1,2,...,n \}$) Entonces gracias a las relaciones de cardeano vieta tenemos que $b_i=(-1)^ia_i$ para $i=1,2,...,n-1$ y $b_n=(-1)^na_n-(-1)^nk=(-1)^na_b+(-1)^{n+1}k$ Entonces $P(x_i,y_1,y_2,...,y_n)=x_i^n+b_1x_i^{n-1}+...+x_ib_{n-1}+b_n=x_i^n-a_1x_i^{n-1}+...+(-1)^{n-1}a_{n-1}x_i+(-1)^na_n+(-1)^{n+1}k=(x_i-x_1)(x_i-x_2)...(x_i-x_n)+(-1)^{n+1}k=(-1)^{n+1}k$ para $i=1,2,...,n$.Volviendo al problema tenemos que todas las filas toman el valor de $k$ (si n es impar) y $-k$ (si n es par).$ Editado: se me fue en algunos detalles, pero ya esta perfecto, no estoy tan deacuerdo en decir que los elementos deben de ser distintos, ademas vi un libro donde lo define exactamente asi (imo compedium) Xd. Mensaje modificado por xD13G0x el Dec 12 2009, 07:44 PM -------------------- "I've never let my school interfere with my education.”

~Fatal_Collapse~ Ver Perfil del Miembro Ver los mensajes de este miembro	Dec 12 2009, 07:08 PM Publicado: #3
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.564 Registrado: 12-November 07 Desde: La Union, XIV Region de los Rios Miembro Nº: 12.607 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Ahora si, solucion correcta Diego =). Realmente una solucion no tan intuitiva pero efectiva a este simpatico problema Saludos y sigue entrenando. -------------------- Ricardo Vargas Obando Ex-alumno Deutsche Schule La Unión (Generación 2010, de los 150 años). Novato de Licenciatura en Matemática/Estadística, en la Pontificia Universidad Católica de Chile. Grupo de facebook de Novatos Matemática y Estadística PUC 2011 Currículum Olímpico: Medalla de Plata, XIX Olimpiada Nacional de Matemática Nivel Menor (2007) Medalla de Oro, XXI Olimpiada Nacional de Matemática Nivel Mayor (2009) Medalla de Bronce, XXV Olimpiada Iberoamericana de Matemática (2010) Medalla de Oro, XXII Olimpiada Nacional de Matemática Nivel Mayor (2010) "What we learned as children, that one plus one equals two, we know to be false. One plus one equals one. We even have a word when you plus another, equals one. That word is love." "Todos piensan en cambiar el mundo, pero nadie piensa en cambiarse a sí mismo."

makmat Ver Perfil del Miembro Ver los mensajes de este miembro	Dec 15 2009, 05:22 PM Publicado: #4
Dios Matemático Supremo Grupo: Moderador Mensajes: 590 Registrado: 14-October 07 Miembro Nº: 11.310 Colegio/Liceo: Universidad: Sexo:	Buuuu hace dias queria postear la solucìón al problema pero creo que se me adelantaron xD: Como sea ahi va mi solución: 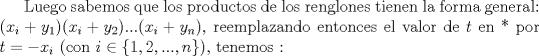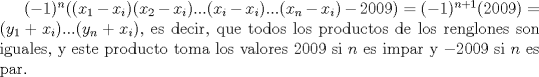$TEX: Los productos de las columnas tienen la forma general: $(x_1+t)(x_2+t)...(x_n+t)=2009$, pero reescribiendolo como sigue: $(x_1+t)(x_2+t)...(x_n+t)-2009=0$, vemos que las raíces de esta ecuación deben ser $n$, pues ese es el grado máximo de la incógnita $t$ es $n$, si nos fijamos bien las raíces de la ecuación son efectivamente los $y_j$, pues esto se deduce del enunciado del problema, es decir, $t \in \{ y_1, y_2,..., y_n \}$, ahora sea $P(t)=(x_1+t)(x_2+t)...(x_n+t)-2009$ (haciendo $P(t)=0$ obtenemos la ecuación anterior), luego el Teorema Fundamental del Álgebra nos asegura que este polinomio $P(t)$, puede ser factorizado como: $P(t)=(t-y_1)(t-y_2)...(t-y_n)$, es decir que $P(t)=(x_1+t)(x_2+t)...(x_n+t)-2009=(t-y_1)(t-y_2)...(t-y_n)$. Luego multiplicando por $(-1)^n$ la última expresión resulta: $(-1)^n ((x_1+t)(x_2+t)...(x_n+t)-2009)=(-1)^n(t-y_1)(t-y_2)...(t-y_n)=(y_1-t)...(y_n-t)$ .$ $TEX: Luego sabemos que los productos de los renglones tienen la forma general: $(x_i+y_1)(x_i+y_2)...(x_i+y_n)$, reemplazando entonces el valor de $t$ en por $t=-x_i$ (con $i \in \{ 1,2,...,n\}$), tenemos :$ $TEX: $(-1)^n ((x_1-x_i)(x_2-x_i)...(x_i-x_i)...(x_n-x_i)-2009)=(-1)^{n+1}(2009)=(y_1+x_i)...(y_n+x_i)$, es decir, que todos los productos de los renglones son iguales, y este producto toma los valores $2009$ si $n$ es impar y $-2009$ si $n$ es par.$ Saludos , me verán rara vez conectado pues, estoy sin computador U________u, pero veremos que puedo hacer por fmat. -------------------- $TEX: $displaystyle oint _{gamma} F cdot dr = displaystyle int int_{R} (dfrac{partial N}{partial x} - dfrac{partial M}{partial y}) dA$$ $TEX: $frac{a+b}{2}ge sqrt{ab}$$ [!] $TEX: $displaystyle int_{Mak^2}^{Mat}Mak^{Mat^{Mak}_{Mat}}dx$$ Doctor en Matemáticas Estudiando y creando problemas $TEX: MakMat$ $TEX: $displaystyle oint_{gamma} F cdot dr= int int_{R} rot F cdot black{N} dS$$ Adiós Kazajstán...

~Fatal_Collapse~ Ver Perfil del Miembro Ver los mensajes de este miembro	Dec 15 2009, 05:56 PM Publicado: #5
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.564 Registrado: 12-November 07 Desde: La Union, XIV Region de los Rios Miembro Nº: 12.607 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Jeje, esta era la idea de solucion que me comentabas en stgo pal problema?? Bonita solucion makmat, si bien es similar en idea a la de xD13G0x la de ocupar polinomios (al igual que la mia), esta solucion se parece mas a la mia, pues no ocupa tan explicitamente Cardano-Vieta. Y bueno, no te preocupes por lo del PC -------------------- Ricardo Vargas Obando Ex-alumno Deutsche Schule La Unión (Generación 2010, de los 150 años). Novato de Licenciatura en Matemática/Estadística, en la Pontificia Universidad Católica de Chile. Grupo de facebook de Novatos Matemática y Estadística PUC 2011 Currículum Olímpico: Medalla de Plata, XIX Olimpiada Nacional de Matemática Nivel Menor (2007) Medalla de Oro, XXI Olimpiada Nacional de Matemática Nivel Mayor (2009) Medalla de Bronce, XXV Olimpiada Iberoamericana de Matemática (2010) Medalla de Oro, XXII Olimpiada Nacional de Matemática Nivel Mayor (2010) "What we learned as children, that one plus one equals two, we know to be false. One plus one equals one. We even have a word when you plus another, equals one. That word is love." "Todos piensan en cambiar el mundo, pero nadie piensa en cambiarse a sí mismo."

makmat Ver Perfil del Miembro Ver los mensajes de este miembro	Dec 17 2009, 06:38 PM Publicado: #6
Dios Matemático Supremo Grupo: Moderador Mensajes: 590 Registrado: 14-October 07 Miembro Nº: 11.310 Colegio/Liceo: Universidad: Sexo:	CITA(Kain #13 @ Dec 15 2009, 07:56 PM) Jeje, esta era la idea de solucion que me comentabas en stgo pal problema?? Bonita solucion makmat, si bien es similar en idea a la de xD13G0x la de ocupar polinomios (al igual que la mia), esta solucion se parece mas a la mia, pues no ocupa tan explicitamente Cardano-Vieta. Y bueno, no te preocupes por lo del PC Esa era la idea, cuando comentabamos te dije lo de trabajar con las raices y bueno me dijiste que por ahi iba, eso si tuve un estancamiento casi al final, luego se me ocurrió multiplicar por -1 a la n y salio xDD, bonito el problema PD: postea tu solucion, los fanaticos queremos verla Saludos y sorry por la respuesta taan atrasada. -------------------- $TEX: $displaystyle oint _{gamma} F cdot dr = displaystyle int int_{R} (dfrac{partial N}{partial x} - dfrac{partial M}{partial y}) dA$$ $TEX: $frac{a+b}{2}ge sqrt{ab}$$ [!] $TEX: $displaystyle int_{Mak^2}^{Mat}Mak^{Mat^{Mak}_{Mat}}dx$$ Doctor en Matemáticas Estudiando y creando problemas $TEX: MakMat$ $TEX: $displaystyle oint_{gamma} F cdot dr= int int_{R} rot F cdot black{N} dS$$ Adiós Kazajstán...

« Posterior · Problemas Resueltos · Anterior »

Reply to this topic

Start new topic

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 4th April 2025 - 02:54 PM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.