|
|
|
|
|
|
|
  |
 Nov 24 2009, 01:41 PM Nov 24 2009, 01:41 PM
Publicado:
#1
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.812 Registrado: 4-November 07 Desde: Santiago Miembro Nº: 12.213 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
![TEX: \noindent Sea $f:U\subseteq \mathbb{R}^3\to \mathbb{R}$, donde $U$ es un abierto, y $\Omega \subset U$ una región de las típicas del Teorema de la Divergencia.\\<br />\\<br />Suponga que $f$ se anula en $\partial \Omega$ y que además es \emph{armónica}, es decir, satisface la ecuación de Laplace:<br />\[\triangle f = \nabla^2 f =0.\]<br />Demuestre que $f$ es la función nula en $\Omega$.<br />](./tex/7f0180f9a2bab7197e3b0eaaec53e325.png) -------------------- |
|
|
|
 Dec 25 2009, 07:08 PM Dec 25 2009, 07:08 PM
Publicado:
#2
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 560 Registrado: 24-December 09 Miembro Nº: 64.629 |
![TEX: \noindent Sea $f:U\subseteq \mathbb{R}^3\to \mathbb{R}$, donde $U$ es un abierto, y $\Omega \subset U$ una región de las típicas del Teorema de la Divergencia.\\<br />\\<br />Suponga que $f$ se anula en $\partial \Omega$ y que además es \emph{armónica}, es decir, satisface la ecuación de Laplace:<br />\[\triangle f = \nabla^2 f =0.\]<br />Demuestre que $f$ es la función nula en $\Omega$.<br />](./tex/7f0180f9a2bab7197e3b0eaaec53e325.png) Vemos al problema como un problema de neumann. Sea 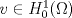 . Multiplicamos la condición de laplace por . Multiplicamos la condición de laplace por  y luego integramos sobre y luego integramos sobre 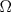 : :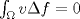 Usando la primera identidad de green se obtiene 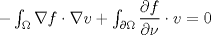 Pero como se anula en la frontera nos queda que 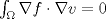 para todo para todo 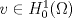 , es decir, se tiene que , es decir, se tiene que 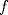 es constante en es constante en 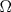 pues el integrando se anula en casi todo punto ( y bla bla bla) pues el integrando se anula en casi todo punto ( y bla bla bla)No se como seguir para que sea nula pero es un avance Mensaje modificado por aleph_omega el Dec 25 2009, 07:15 PM |
|
|
|
 Dec 25 2009, 10:11 PM Dec 25 2009, 10:11 PM
Publicado:
#3
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.812 Registrado: 4-November 07 Desde: Santiago Miembro Nº: 12.213 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
No me manejo con Neumann (EDP?). Pero de lo que logré entender, la idea va por ahí
-------------------- |
|
|
|
 Dec 25 2009, 10:36 PM Dec 25 2009, 10:36 PM
Publicado:
#4
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 560 Registrado: 24-December 09 Miembro Nº: 64.629 |
El problema de neumman es un problema de valores de contorno de la forma
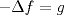 en en 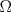 con la condicion de frontera 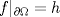 Cuando 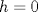 el problema es el problema homogeneo. Asocié tu problema como un problema de neumann homogeneo con el problema es el problema homogeneo. Asocié tu problema como un problema de neumann homogeneo con 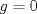 y aplique la formulación variacional al problema de neumann donde ahi se involucran las identidades de green. y aplique la formulación variacional al problema de neumann donde ahi se involucran las identidades de green.pd: El problema de Neumann deberia verse en cualquier curso básico de ecuaciones en derivadas parciales. Lo de las formulaciones variaciones ya es análisis funcional ( involucre el espacio de sobolev 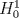 que son las funciones en que son las funciones en 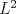 tales que su derivada debil vive en tales que su derivada debil vive en 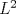 y ademas se anulan en la frontera). y ademas se anulan en la frontera).
Mensaje modificado por aleph_omega el Dec 25 2009, 10:42 PM |
|
|
|
 Oct 3 2010, 11:53 PM Oct 3 2010, 11:53 PM
Publicado:
#5
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 832 Registrado: 11-September 07 Desde: París, Francia Miembro Nº: 10.056 Nacionalidad:  Sexo:  |

Mensaje modificado por nmg1302 el Oct 4 2010, 02:06 PM |
|
|
|
 Jan 27 2011, 02:59 PM Jan 27 2011, 02:59 PM
Publicado:
#6
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.812 Registrado: 4-November 07 Desde: Santiago Miembro Nº: 12.213 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Bien!
-------------------- |
|
|
|
 Apr 22 2011, 03:46 PM Apr 22 2011, 03:46 PM
Publicado:
#7
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 560 Registrado: 24-December 09 Miembro Nº: 64.629 |
Por el principio del maximo y minimo para funciones armónicas sale en un paso!
|
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 25th April 2025 - 11:51 PM |






![TEX: \[\mathfrak{L}=\int_{-\infty}^\infty e^{-289x^2}dx=\frac{\Gamma (\frac{1}{2})}{17}=\frac{\sqrt{\pi}}{17}\]](./tex/e0e88dba678ca3ead120b088f41191b2.png)







