|
|
|
|
|
|
|
  |
 Nov 16 2009, 04:41 PM Nov 16 2009, 04:41 PM
Publicado:
#1
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.179 Registrado: 4-January 08 Desde: La Florida Miembro Nº: 14.344 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Adjunto Control de matemáticas generales, sería de gran ayuda para este usuario que el control se desarrollara xD
 Controlmatgen.pdf ( 72.39k )
Número de descargas: 96
Controlmatgen.pdf ( 72.39k )
Número de descargas: 96Mensaje modificado por FelipeAcr el Nov 16 2009, 04:43 PM |
|
|
|
 Nov 20 2009, 04:42 PM Nov 20 2009, 04:42 PM
Publicado:
#2
|
|
|
Maestro Matemático Grupo: Usuario FMAT Mensajes: 77 Registrado: 16-July 09 Desde: Scuni Miembro Nº: 55.693 Nacionalidad:  Universidad:  Sexo:  |
![TEX: <br /><br />$$<br />\begin{array}{rccl}<br />T:&M(2,\mathbb{R})&\longrightarrow&M(2,\mathbb{R})\\<br />&\left( \begin{array}{cc}<br />a & b \\<br />c & d <br />\end{array}<br />\right)&\mapsto&\left( \begin{array}{cc}<br />a-c & b-d \\<br />2c-2a & 2d-2b <br />\end{array}<br />\right)<br />\end{array} <br />$$<br /><br />a) sea $v=\left( \begin{array}{cc}<br />a & b \\<br />c & d <br />\end{array}<br />\right) \in Ker(T) \Longrightarrow T(v)=0$\\<br /><br />$$T\left[\left( \begin{array}{cc}<br />a & b \\<br />c & d <br />\end{array}<br />\right)\right]=\left( \begin{array}{cc}<br />a-c & b-d \\<br />2c-2a & 2d-2b <br />\end{array}<br />\right)=\left( \begin{array}{cc}<br />0 & 0 \\<br />0 & 0 <br />\end{array}<br />\right)$$<br /><br />$\left\{\begin{array}{c}<br />a=c\\<br />b=d\\<br />2c=2a\\<br />2d=2b<br />\end{array}\right.$ \\<br /><br /><br /> <br /><br />por lo tanto: $Ker(T)=\left\{\left( \begin{array}{cc}<br />a & b \\<br />a & b <br />\end{array}<br />\right)\;\;/a,b \in \mathbb{R}\right\}$\\<br /><br />asi el $ker(T)$ se puede escribir como combinacion lineal de los vectores:<br /><br />$$\left( \begin{array}{cc}<br />a & b \\<br />a & b <br />\end{array}<br />\right)=a\left( \begin{array}{cc}<br />1 & 0 \\<br />1 & 0 <br />\end{array}<br />\right)+b\left( \begin{array}{cc}<br />0 & 1 \\<br />0 & 1 <br />\end{array}<br />\right)$$<br /><br />entonces el generador del $ker(T)$ es: $\left\langle \left( \begin{array}{cc}<br />1 & 0 \\<br />1 & 0 <br />\end{array}<br />\right); \left (\begin{array}{cc}<br />0 & 1 \\<br />0 & 1 <br />\end{array}<br />\right)\right\rangle$\\<br /><br /><br />por tanto el conjunto es linealmente independiente. Como el conjunto es una base del $Ker(T)$ entonces $dim Ker(T)=2$\\<br /><br /><br /><br /><br /><br />](./tex/fdb1e2e8588a05e059e1a31ce7d5c504.png) -------------------- "Describiendo el movimiento de los electrones"
Voluntad,Trabajo, Pasión  Departamento de ingenieria eléctrica |
|
|
|
 Nov 20 2009, 06:04 PM Nov 20 2009, 06:04 PM
Publicado:
#3
|
|
|
Maestro Matemático Grupo: Usuario FMAT Mensajes: 77 Registrado: 16-July 09 Desde: Scuni Miembro Nº: 55.693 Nacionalidad:  Universidad:  Sexo:  |
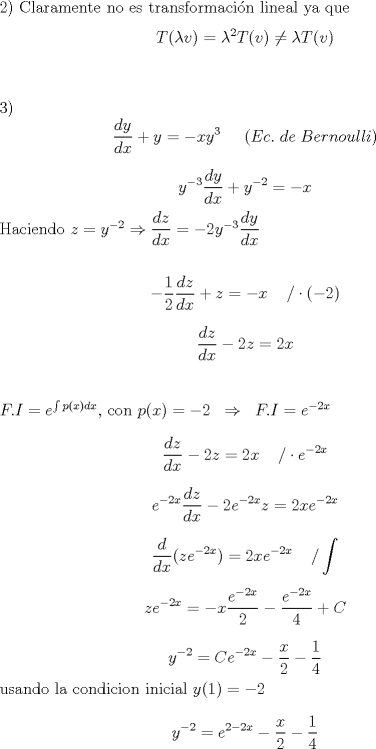 -------------------- "Describiendo el movimiento de los electrones"
Voluntad,Trabajo, Pasión  Departamento de ingenieria eléctrica |
|
|
|
 Jan 5 2016, 10:57 AM Jan 5 2016, 10:57 AM
Publicado:
#4
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 579 Registrado: 17-April 11 Miembro Nº: 87.233 Colegio/Liceo:  Universidad:  Sexo:  |
4.
5. |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 18th October 2025 - 11:49 AM |










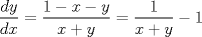
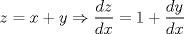
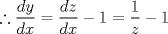
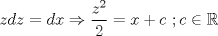
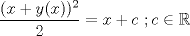
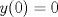 se llega a que
se llega a que