|
|
|
|
|
|
|
  |
 Oct 2 2009, 09:13 PM Oct 2 2009, 09:13 PM
Publicado:
#1
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.564 Registrado: 12-November 07 Desde: La Union, XIV Region de los Rios Miembro Nº: 12.607 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
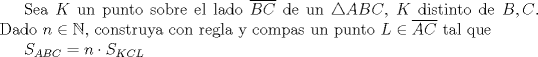 (*) 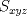 es el area del triangulo XYZ. es el area del triangulo XYZ.
-------------------- Ricardo Vargas Obando
Ex-alumno Deutsche Schule La Unión (Generación 2010, de los 150 años). Novato de Licenciatura en Matemática/Estadística, en la Pontificia Universidad Católica de Chile.  Grupo de facebook de Novatos Matemática y Estadística PUC 2011 Currículum Olímpico:
|
|
|
|
 Feb 16 2011, 11:03 AM Feb 16 2011, 11:03 AM
Publicado:
#2
|
|
 Dios Matemático Supremo Grupo: Team Ensayos FMAT Mensajes: 513 Registrado: 25-April 08 Desde: CSMC Miembro Nº: 21.189 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Esta solucion supone conocido el valor de un trazo unitario. Entonces.
Tenemos nuestro triangulo de lados 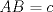 , , 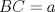 y y 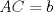 , y el punto , y el punto 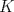 es tal que se encuentra a una distancia es tal que se encuentra a una distancia 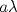 de de 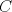  116.jpg ( 9.5k )
Número de descargas: 0
116.jpg ( 9.5k )
Número de descargas: 0Sea 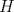 la altura del triangulo desde la altura del triangulo desde 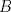 y y 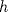 la proyeccion de la proyeccion de 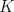 sobre sobre 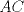  117.jpg ( 12.02k )
Número de descargas: 0
117.jpg ( 12.02k )
Número de descargas: 0Tenemos que 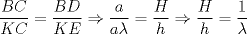 Si el punto 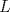 se encuentra a una distancia se encuentra a una distancia  de de 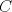 ... ... 118.jpg ( 13.39k )
Número de descargas: 0
118.jpg ( 13.39k )
Número de descargas: 0...lo que necesitamos es que, dado 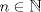 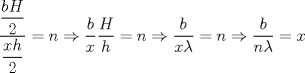 Entonces, lambda lo obtenemos de la siguiente manera:  119.jpg ( 18.02k )
Número de descargas: 0
119.jpg ( 18.02k )
Número de descargas: 0En 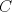 ubicamos un segmento unitario y al extremo le llamamos ubicamos un segmento unitario y al extremo le llamamos 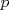 . Unimos . Unimos 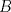 con con 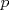 y por y por 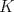 trazamos una paralela a trazamos una paralela a 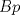 tal que corta a tal que corta a 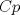 en en 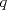 . Entonces tenemos que: . Entonces tenemos que: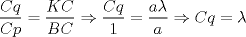 Ahora copiamos  veces el segmento veces el segmento 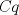 tal que tal que 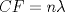  120.jpg ( 16.01k )
Número de descargas: 0
120.jpg ( 16.01k )
Número de descargas: 0Finalmente lo que hacemos es establecer un trazo 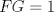 , unir , unir 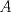 con con 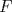 y trazar una paralela a y trazar una paralela a 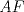 por por 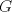 cortando a la extencion de cortando a la extencion de 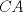 en en 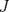  121.jpg ( 22.34k )
Número de descargas: 0
121.jpg ( 22.34k )
Número de descargas: 0Entonces por el teorema de Thales tenemos que 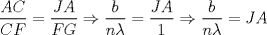 . .  122.jpg ( 14.98k )
Número de descargas: 0
122.jpg ( 14.98k )
Número de descargas: 0Ubicamos esta distancia adyacente a 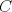 y el problema esta resuelto. y el problema esta resuelto.
Archivo(s) Adjunto(s)
-------------------- FunGeometry
SIEMPRE CON LAS MEJORES INTENCIONES DE AYUDAR. ATTE. NABODORBUCO EL TERCER OJO GoGeometry LA IDEA ES QUE NO ESPERES QUE FMAT RESUELVA TUS TAREAS, ESCRIBE SIEMPRE CUALES SON TUS INQUIETUDES |
|
|
|
 Jul 6 2011, 10:32 PM Jul 6 2011, 10:32 PM
Publicado:
#3
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.564 Registrado: 12-November 07 Desde: La Union, XIV Region de los Rios Miembro Nº: 12.607 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Perfecto!!!!!
Así que PS: Sorry por la demora -------------------- Ricardo Vargas Obando
Ex-alumno Deutsche Schule La Unión (Generación 2010, de los 150 años). Novato de Licenciatura en Matemática/Estadística, en la Pontificia Universidad Católica de Chile.  Grupo de facebook de Novatos Matemática y Estadística PUC 2011 Currículum Olímpico:
|
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 3rd April 2025 - 09:01 PM |







