 Sub grupos, multiplos n y m de Z |
|
|
|
|
|
|
Foro fmat.cl > Programa Enseñanza Universitaria > Consultas > Banco de Problemas Resueltos > Álgebra Abstracta  |
 Sep 24 2009, 04:56 PM
Publicado:
#1
|
|
|
Maestro Matemático  Grupo: Usuario FMAT Mensajes: 74 Registrado: 14-May 08 Desde: Santa Cruz Miembro Nº: 23.117 Nacionalidad:  Universidad:  Sexo:   |
|
 |
 
|
|
Sep 24 2009, 06:56 PM
Publicado:
#2
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.818 Registrado: 21-December 06 Miembro Nº: 3.434 |
Se pueden decir muchas cosas así que yo creo que sería mejor que TU partieras diciendo algo.
-------------------- |
|
|
|
|
Sep 24 2009, 11:53 PM
Publicado:
#3
|
|
|
Maestro Matemático Grupo: Usuario FMAT Mensajes: 74 Registrado: 14-May 08 Desde: Santa Cruz Miembro Nº: 23.117 Nacionalidad: Universidad: Sexo: |
El titulo del tema es sub grupos
disculpa si no espacifique mas si conoces del tema quisas me puedas ayudar con otro problema que propuse y no lo hallo |
|
|
|
|
Sep 24 2009, 11:54 PM
Publicado:
#4
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.818 Registrado: 21-December 06 Miembro Nº: 3.434 |
Si te puedo ayudar, pero no quiero que no pienses nada
 Tienes alguna idea de que podrías hacer? Fijarse en los divisores comunes de n y m podría ayudarte. -------------------- |
|
|
|
|
Sep 25 2009, 11:01 AM
Publicado:
#5
|
|
|
Maestro Matemático Grupo: Usuario FMAT Mensajes: 74 Registrado: 14-May 08 Desde: Santa Cruz Miembro Nº: 23.117 Nacionalidad: Universidad: Sexo: |
ya no es necesario
gracias |
|
|
|
|
Mar 24 2010, 11:43 PM
Publicado:
#6
|
|
|
Dios Matemático Supremo  Grupo: Super Moderador Mensajes: 2.065 Registrado: 25-May 08 Desde: Pelotillehue Miembro Nº: 24.463 |
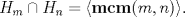
-------------------- "Please forget everything you have learned in school; for you haven't learned it... Please keep in mind at all times the corresponding portions of your school curriculum; for you haven't actually forgotten them." -- E. Landau
|
|
|
|
|
Nov 29 2010, 05:12 PM
Publicado:
#7
|
|
|
Principiante Matemático Grupo: Usuario FMAT Mensajes: 2 Registrado: 29-November 10 Miembro Nº: 80.915 Nacionalidad:  Sexo: |
como se demuestra que su interseccion es un grupo o sea si H intersecta a K por ponerle nombre al otro grupo
Tiene que existir en ambos un x Elemento de H que tambn pertenesca a K |
|
|
|
|
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 3rd April 2025 - 11:49 PM |
