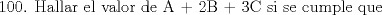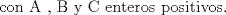P100 - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Sector Preparación Olimpiadas > Competencias y Olimpiadas > El Gran Desafío > El Gran Desafio VII > Problemas Resueltos

Reply to this topic

Start new topic

P100

Newtype Ver Perfil del Miembro Ver los mensajes de este miembro	Sep 14 2009, 08:43 PM Publicado: #1
Dios Matemático Supremo Grupo: Team Ensayos FMAT Mensajes: 1.559 Registrado: 18-November 07 Miembro Nº: 12.754 Nacionalidad: Sexo:	$TEX: 100. Hallar el valor de A + 2B + 3C si se cumple que$ P100.jpg ( 2.36k ) Número de descargas: 1 $TEX: con A , B y C enteros positivos.$ -------------------- Empezando con Desigualdades? Encuentra aquí problemas resueltos

Kaissa Ver Perfil del Miembro Ver los mensajes de este miembro	Feb 1 2010, 09:53 PM Publicado: #2
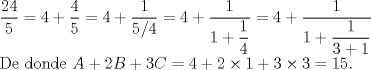
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad: Colegio/Liceo: Sexo:	$TEX: $ $\\<br />$\dfrac{24}{5}=4+\dfrac{4}{5}=4+\dfrac{1}{5/4}=4+\dfrac{1}{1+\dfrac{1}{4}}=4+\dfrac{1}{1+\dfrac{1}{3+1}}$\\<br />De donde $A+2B+3C=4+2\times1+3\times3=15$.<br />$ Mensaje modificado por Kaissa el Feb 1 2010, 09:55 PM -------------------- Este es un extracto de Qué es fmat by Kenshin. La pregunta para ti estimado(a) lector(a) es... ¿Qué haces tu para que ésto se cumpla?

~Fatal_Collapse~ Ver Perfil del Miembro Ver los mensajes de este miembro	Feb 1 2010, 10:13 PM Publicado: #3
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.564 Registrado: 12-November 07 Desde: La Union, XIV Region de los Rios Miembro Nº: 12.607 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	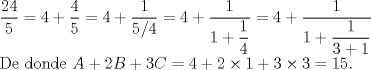CITA(Kaissa @ Feb 1 2010, 11:53 PM) $TEX: $ $\\<br />$\dfrac{24}{5}=4+\dfrac{4}{5}=4+\dfrac{1}{5/4}=4+\dfrac{1}{1+\dfrac{1}{4}}=4+\dfrac{1}{1+\dfrac{1}{3+1}}$\\<br />De donde $A+2B+3C=4+2\times1+3\times3=15$.<br />$ Solucion correcta, Kaissa. Aunque por algun motivo me parece haber visto somewhere este problema, o con los mismos numeros xD. En fin, como no tengo link, es solo una conjetura sin demostracion. Con respecto a los problemas del gran desafio, me he percatado que hay varios que se repiten, Hamon (quien aporto con los enunciados y participo destacadamente el año pasado) es mi testigo A resueltos -------------------- Ricardo Vargas Obando Ex-alumno Deutsche Schule La Unión (Generación 2010, de los 150 años). Novato de Licenciatura en Matemática/Estadística, en la Pontificia Universidad Católica de Chile. Grupo de facebook de Novatos Matemática y Estadística PUC 2011 Currículum Olímpico: Medalla de Plata, XIX Olimpiada Nacional de Matemática Nivel Menor (2007) Medalla de Oro, XXI Olimpiada Nacional de Matemática Nivel Mayor (2009) Medalla de Bronce, XXV Olimpiada Iberoamericana de Matemática (2010) Medalla de Oro, XXII Olimpiada Nacional de Matemática Nivel Mayor (2010) "What we learned as children, that one plus one equals two, we know to be false. One plus one equals one. We even have a word when you plus another, equals one. That word is love." "Todos piensan en cambiar el mundo, pero nadie piensa en cambiarse a sí mismo."

Newtype Ver Perfil del Miembro Ver los mensajes de este miembro	Feb 1 2010, 10:22 PM Publicado: #4
Dios Matemático Supremo Grupo: Team Ensayos FMAT Mensajes: 1.559 Registrado: 18-November 07 Miembro Nº: 12.754 Nacionalidad: Sexo:	CITA(~Fatal_Collapse~ @ Feb 1 2010, 11:13 PM) Solucion correcta, Kaissa. Aunque por algun motivo me parece haber visto somewhere este problema, o con los mismos numeros xD. En fin, como no tengo link, es solo una conjetura sin demostracion. Con respecto a los problemas del numero de oro, me he percatado que hay varios que se repiten, Hamon (quien aporto con los enunciados y participo destacadamente el año pasado) es mi testigo A resueltos es el gran desafio ...y si, comparando con versiones anteriores se pueden ver varios problemas repetidos...sera ahi donde los habras visto creo -------------------- Empezando con Desigualdades? Encuentra aquí problemas resueltos

Kaissa Ver Perfil del Miembro Ver los mensajes de este miembro	Feb 1 2010, 10:30 PM Publicado: #5
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad: Colegio/Liceo: Sexo:	otra cosa que cabe destacar es que hay problemas de dificultad bastante brutal respecto de otros incluso de numeracion consecutiva xd lo que hace entretenida la lectura de los mismos. -------------------- Este es un extracto de Qué es fmat by Kenshin. La pregunta para ti estimado(a) lector(a) es... ¿Qué haces tu para que ésto se cumpla?

Newtype Ver Perfil del Miembro Ver los mensajes de este miembro	Feb 4 2010, 11:43 PM Publicado: #6
Dios Matemático Supremo Grupo: Team Ensayos FMAT Mensajes: 1.559 Registrado: 18-November 07 Miembro Nº: 12.754 Nacionalidad: Sexo:	CITA(Kaissa @ Feb 1 2010, 11:30 PM) otra cosa que cabe destacar es que hay problemas de dificultad bastante brutal respecto de otros incluso de numeracion consecutiva xd lo que hace entretenida la lectura de los mismos. obvio, no estan para nada ordenados por dificultad...de hecho el orden cuando te inscribes en la paginaes aleatorio xD -------------------- Empezando con Desigualdades? Encuentra aquí problemas resueltos

« Posterior · Problemas Resueltos · Anterior »

Reply to this topic

Start new topic

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 23rd November 2024 - 08:14 PM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.