P077 - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Sector Preparación Olimpiadas > Competencias y Olimpiadas > El Gran Desafío > El Gran Desafio VII > Problemas Resueltos

Reply to this topic

Start new topic

P077

Newtype Ver Perfil del Miembro Ver los mensajes de este miembro	Sep 14 2009, 11:18 AM Publicado: #1
Dios Matemático Supremo Grupo: Team Ensayos FMAT Mensajes: 1.559 Registrado: 18-November 07 Miembro Nº: 12.754 Nacionalidad: Sexo:	$TEX: 77. Si cada número de la secuencia 5, A, B, 26, C es el promedio de los dos que le rodean. ¿Cuál es el valor de A + B + C?$ -------------------- Empezando con Desigualdades? Encuentra aquí problemas resueltos

TamaruKaT Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 24 2010, 06:22 PM Publicado: #2
Dios Matemático Grupo: Team Ensayos FMAT Mensajes: 287 Registrado: 4-June 07 Miembro Nº: 6.414 Nacionalidad: Sexo:	$TEX: \[<br />\begin{gathered}<br /> \left. {\underline {\, <br /> \begin{gathered}<br /> a)\frac{{5 + B}}<br />{2} = A \hfill \\<br /> b)\frac{{A + 26}}<br />{2} = B \hfill \\<br /> c)\frac{{B + C}}<br />{2} = 26 \hfill \\ <br />\end{gathered} \,}}\! \right\| \hfill \\<br /> {\text{Primera forma}} \hfill \\<br /> {\text{reemplazamos la ecuacion a) en la ecuacion b)}} \hfill \\<br /> \frac{{\frac{{5 + B}}<br />{2} + 26}}<br />{2} = B \hfill \\<br /> \hfill \\<br /> \frac{{5 + B + 52}}<br />{2} = 2B \hfill \\<br /> \hfill \\<br /> B + 57 = 4B \hfill \\<br /> B = 19 \hfill \\ <br />\end{gathered} <br />\]$ $TEX: \[\begin{gathered}<br /> {\text{Ahora que tenemos B}}{\text{, lo reemplazamos en el resto de las ecuaciones}}... \hfill \\<br /> \frac{{5 + 19}}<br />{2} = A \hfill \\<br /> 24 = 2A \hfill \\<br /> A = 12 \hfill \\<br /> \hfill \\<br /> \frac{{19 + C}}<br />{2} = 26 \hfill \\<br /> 19 + C = 52 \hfill \\<br /> C = 33 \hfill \\ <br />\end{gathered}\]$ $TEX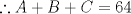: $ \therefore A+B+C=64$$ _______________________________________________ $TEX: \[<br />\begin{gathered}<br /> {\text{Otra forma de realiazarlo es la siguiente}}... \hfill \\<br /> {\text{Ocupamos la ecuacion c)}} \hfill \\<br /> \frac{{B + C}}<br />{2} = 26 \hfill \\<br /> {\text{Con la que determinamos el valor de B + C}} \hfill \\<br /> B + C = 52 \hfill \\<br /> {\text{Ahora tomamos la ecuacion b) y la reemplazamos en la a)}} \hfill \\<br /> \frac{{5 + \frac{{A + 26}}<br />{2}}}<br />{2} = A \hfill \\<br /> \frac{{10 + A + 26}}<br />{2} = 2A \hfill \\<br /> 36 + A = 4A \hfill \\<br /> A = 12 \hfill \\<br /> \hfill \\<br /> {\text{Conociendo los valores de }}A{\text{ y }}B + C{\text{ llegamos a que }}A + B + C = 64 \hfill \\ <br />\end{gathered} <br />\]$ --------------------

~Fatal_Collapse~ Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 24 2010, 07:31 PM Publicado: #3
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.564 Registrado: 12-November 07 Desde: La Union, XIV Region de los Rios Miembro Nº: 12.607 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(TamaruKaT @ Jan 24 2010, 08:22 PM) $TEX: \[<br />\begin{gathered}<br /> \left. {\underline {\, <br /> \begin{gathered}<br /> a)\frac{{5 + B}}<br />{2} = A \hfill \\<br /> b)\frac{{A + 26}}<br />{2} = B \hfill \\<br /> c)\frac{{B + C}}<br />{2} = 26 \hfill \\ <br />\end{gathered} \,}}\! \right\| \hfill \\<br /> {\text{Primera forma}} \hfill \\<br /> {\text{reemplazamos la ecuacion a) en la ecuacion b)}} \hfill \\<br /> \frac{{\frac{{5 + B}}<br />{2} + 26}}<br />{2} = B \hfill \\<br /> \hfill \\<br /> \frac{{5 + B + 52}}<br />{2} = 2B \hfill \\<br /> \hfill \\<br /> B + 57 = 4B \hfill \\<br /> B = 19 \hfill \\ <br />\end{gathered} <br />\]$ $TEX: \[\begin{gathered}<br /> {\text{Ahora que tenemos B}}{\text{, lo reemplazamos en el resto de las ecuaciones}}... \hfill \\<br /> \frac{{5 + 19}}<br />{2} = A \hfill \\<br /> 24 = 2A \hfill \\<br /> A = 12 \hfill \\<br /> \hfill \\<br /> \frac{{19 + C}}<br />{2} = 26 \hfill \\<br /> 19 + C = 52 \hfill \\<br /> C = 33 \hfill \\ <br />\end{gathered}\]$ $TEX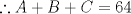: $ \therefore A+B+C=64$$ _______________________________________________ $TEX: \[<br />\begin{gathered}<br /> {\text{Otra forma de realiazarlo es la siguiente}}... \hfill \\<br /> {\text{Ocupamos la ecuacion c)}} \hfill \\<br /> \frac{{B + C}}<br />{2} = 26 \hfill \\<br /> {\text{Con la que determinamos el valor de B + C}} \hfill \\<br /> B + C = 52 \hfill \\<br /> {\text{Ahora tomamos la ecuacion b) y la reemplazamos en la a)}} \hfill \\<br /> \frac{{5 + \frac{{A + 26}}<br />{2}}}<br />{2} = A \hfill \\<br /> \frac{{10 + A + 26}}<br />{2} = 2A \hfill \\<br /> 36 + A = 4A \hfill \\<br /> A = 12 \hfill \\<br /> \hfill \\<br /> {\text{Conociendo los valores de }}A{\text{ y }}B + C{\text{ llegamos a que }}A + B + C = 64 \hfill \\ <br />\end{gathered} <br />\]$ Si seguimos asi.... parece que alguien se acabara el sector Respuestas correctas srta Tamara =), asi que paso a resueltos -------------------- Ricardo Vargas Obando Ex-alumno Deutsche Schule La Unión (Generación 2010, de los 150 años). Novato de Licenciatura en Matemática/Estadística, en la Pontificia Universidad Católica de Chile. Grupo de facebook de Novatos Matemática y Estadística PUC 2011 Currículum Olímpico: Medalla de Plata, XIX Olimpiada Nacional de Matemática Nivel Menor (2007) Medalla de Oro, XXI Olimpiada Nacional de Matemática Nivel Mayor (2009) Medalla de Bronce, XXV Olimpiada Iberoamericana de Matemática (2010) Medalla de Oro, XXII Olimpiada Nacional de Matemática Nivel Mayor (2010) "What we learned as children, that one plus one equals two, we know to be false. One plus one equals one. We even have a word when you plus another, equals one. That word is love." "Todos piensan en cambiar el mundo, pero nadie piensa en cambiarse a sí mismo."

« Posterior · Problemas Resueltos · Anterior »

Reply to this topic

Start new topic

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 4th April 2025 - 05:00 AM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.