 P067 |
|
|
|
|
|
|
Foro fmat.cl > Sector Preparación Olimpiadas > Competencias y Olimpiadas > El Gran Desafío > El Gran Desafio VII > P41-P80  |
 Sep 14 2009, 11:13 AM
Publicado:
#1
|
|
 Dios Matemático Supremo  Grupo: Team Ensayos FMAT Mensajes: 1.559 Registrado: 18-November 07 Miembro Nº: 12.754 Nacionalidad:  Sexo:   |
-------------------- Empezando con Desigualdades? Encuentra aquí problemas resueltos
|
 |
 
|
|
Jul 20 2014, 03:35 PM
Publicado:
#2
|
|
 Dios Matemático Supremo  Grupo: Usuario FMAT Mensajes: 783 Registrado: 23-April 13 Desde: Constitución Miembro Nº: 118.027 Nacionalidad: Universidad:  Sexo: |
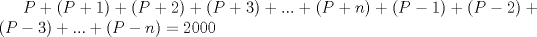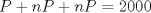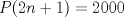   ahora hay que notar que el producto de P por un numero impar es 2000, notando que 5, 25 y 125 son los divisores impares de 2000, probamos, pero solo el 125 cumple que para P, sus cifras sean un numero impar: P=16 Mensaje modificado por juancodmw el Jul 20 2014, 04:18 PM --------------------    |
|
|
|
|
Jul 20 2014, 03:58 PM
Publicado:
#3
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad: Colegio/Liceo:  Sexo:  |
El enunciado está harto mal redactado!
Debería ser "... y que cumple con la propiedad de que existen un natural n tal que al sumar P con los n naturales a la derecha de él y los n naturales a la izquierda de él resulta 2000" pero afortunadamente comprendiste bien el contexto. -------------------- |
|
|
|
|
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 4th April 2025 - 05:02 AM |
