|
|
|
|
|
|
|
  |
 Sep 13 2009, 10:28 PM Sep 13 2009, 10:28 PM
Publicado:
#1
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.564 Registrado: 12-November 07 Desde: La Union, XIV Region de los Rios Miembro Nº: 12.607 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |

-------------------- Ricardo Vargas Obando
Ex-alumno Deutsche Schule La Unión (Generación 2010, de los 150 años). Novato de Licenciatura en Matemática/Estadística, en la Pontificia Universidad Católica de Chile.  Grupo de facebook de Novatos Matemática y Estadística PUC 2011 Currículum Olímpico:
|
|
|
|
 Dec 8 2009, 06:02 PM Dec 8 2009, 06:02 PM
Publicado:
#2
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 288 Registrado: 25-August 09 Desde: Por ahí Miembro Nº: 57.644 Nacionalidad:  Universidad:  Sexo:  |
Offtopic: Ahora sí, espero que no salgan posts repetidos. xD
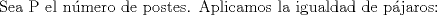  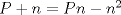 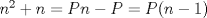 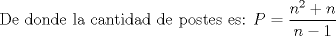
Mensaje modificado por OckUC el Dec 8 2009, 06:02 PM -------------------- RECURSIÓN: Si no lo entiende, vea RECURSIÓN
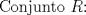     |
|
|
|
 Dec 8 2009, 06:46 PM Dec 8 2009, 06:46 PM
Publicado:
#3
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.564 Registrado: 12-November 07 Desde: La Union, XIV Region de los Rios Miembro Nº: 12.607 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Ya hallaste una ecuacion para el problema, pero aqui es donde llegamos a la parte intedezante. Tienes que
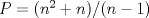 , pero por una cuestion "intuitiva", la cantidad de postes es un entero positivo. Entonces la interrogante es que valores de , pero por una cuestion "intuitiva", la cantidad de postes es un entero positivo. Entonces la interrogante es que valores de  hacen que hacen que 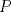 sea natural, y cuanto vale sea natural, y cuanto vale 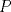 entonces? Hasta ahora va todo bien, pero aun falta lo que te señale entonces? Hasta ahora va todo bien, pero aun falta lo que te señaleSaludos -------------------- Ricardo Vargas Obando
Ex-alumno Deutsche Schule La Unión (Generación 2010, de los 150 años). Novato de Licenciatura en Matemática/Estadística, en la Pontificia Universidad Católica de Chile.  Grupo de facebook de Novatos Matemática y Estadística PUC 2011 Currículum Olímpico:
|
|
|
|
 Dec 8 2009, 07:04 PM Dec 8 2009, 07:04 PM
Publicado:
#4
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 288 Registrado: 25-August 09 Desde: Por ahí Miembro Nº: 57.644 Nacionalidad:  Universidad:  Sexo:  |
Ya hallaste una ecuacion para el problema, pero aqui es donde llegamos a la parte intedezante. Tienes que 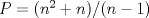 , pero por una cuestion "intuitiva", la cantidad de postes es un entero positivo. Entonces la interrogante es que valores de , pero por una cuestion "intuitiva", la cantidad de postes es un entero positivo. Entonces la interrogante es que valores de  hacen que hacen que 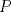 sea natural, y cuanto vale sea natural, y cuanto vale 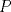 entonces? Hasta ahora va todo bien, pero aun falta lo que te señale entonces? Hasta ahora va todo bien, pero aun falta lo que te señaleSaludos  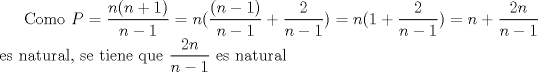 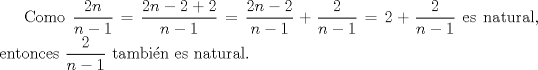  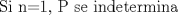 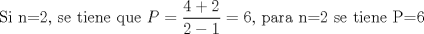 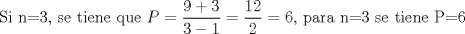 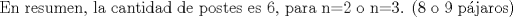
Mensaje modificado por OckUC el Dec 8 2009, 07:06 PM -------------------- RECURSIÓN: Si no lo entiende, vea RECURSIÓN
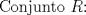     |
|
|
|
 Dec 8 2009, 08:32 PM Dec 8 2009, 08:32 PM
Publicado:
#5
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.564 Registrado: 12-November 07 Desde: La Union, XIV Region de los Rios Miembro Nº: 12.607 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Nada mas que acotar, con eso ya estamos en condiciones de enviar a resueltos.
Saludos -------------------- Ricardo Vargas Obando
Ex-alumno Deutsche Schule La Unión (Generación 2010, de los 150 años). Novato de Licenciatura en Matemática/Estadística, en la Pontificia Universidad Católica de Chile.  Grupo de facebook de Novatos Matemática y Estadística PUC 2011 Currículum Olímpico:
|
|
|
|
 Dec 8 2009, 09:13 PM Dec 8 2009, 09:13 PM
Publicado:
#6
|
|
 Dios Matemático Supremo Grupo: Moderador Mensajes: 590 Registrado: 14-October 07 Miembro Nº: 11.310 Colegio/Liceo:  Universidad:  Sexo:  |
Se podía incluso proceder de la siguiente manera:
 Espero se entienda -------------------- |
|
|
|
 Dec 10 2009, 01:09 PM Dec 10 2009, 01:09 PM
Publicado:
#7
|
|
 Dios Matemático Supremo Grupo: Team Ensayos FMAT Mensajes: 1.559 Registrado: 18-November 07 Miembro Nº: 12.754 Nacionalidad:  Sexo:  |
muy bien OckUC! es bastante complicado cachar como se plantea el problema para despues poder seguir
wen aporte makmat, respuesta precisa y concisa -------------------- Empezando con Desigualdades? Encuentra aquí problemas resueltos
|
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 4th April 2025 - 05:03 AM |