P02 - Foro fmat.cl

P02

Opciones

~Fatal_Collapse~ Ver Perfil del Miembro Ver los mensajes de este miembro	Sep 13 2009, 09:49 PM Publicado: #1
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.564 Registrado: 12-November 07 Desde: La Union, XIV Region de los Rios Miembro Nº: 12.607 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	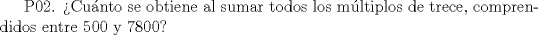$TEX: P02. ¿Cuánto se obtiene al sumar todos los múltiplos de trece, comprendidos entre 500 y 7800?<br /><br />$ -------------------- Ricardo Vargas Obando Ex-alumno Deutsche Schule La Unión (Generación 2010, de los 150 años). Novato de Licenciatura en Matemática/Estadística, en la Pontificia Universidad Católica de Chile. Grupo de facebook de Novatos Matemática y Estadística PUC 2011 Currículum Olímpico: Medalla de Plata, XIX Olimpiada Nacional de Matemática Nivel Menor (2007) Medalla de Oro, XXI Olimpiada Nacional de Matemática Nivel Mayor (2009) Medalla de Bronce, XXV Olimpiada Iberoamericana de Matemática (2010) Medalla de Oro, XXII Olimpiada Nacional de Matemática Nivel Mayor (2010) "What we learned as children, that one plus one equals two, we know to be false. One plus one equals one. We even have a word when you plus another, equals one. That word is love." "Todos piensan en cambiar el mundo, pero nadie piensa en cambiarse a sí mismo."

EnemyOfGod286 Ver Perfil del Miembro Ver los mensajes de este miembro	Feb 12 2010, 06:04 PM Publicado: #2
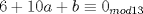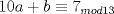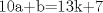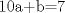Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 858 Registrado: 20-August 09 Desde: In my House Miembro Nº: 57.323 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Debemos hallar el menor multiplo de 13 que sea mayor que 500. $TEX: $$500+10a+b\equiv 0_{mod13}$$$ $TEX: $$6+10a+b\equiv 0_{mod13}$$$ $TEX: $$10a+b\equiv 7_{mod13}$$$ Entonces $TEX: 10a+b=13k+7$ , Si k=0, entonces $TEX: 10a+b=7$ Por lo que a=0 y b=7 Entonces el numero buscado es 507 y es igual a 1339 Ahora notemos que 78 es 136, por lo tanto 7800=13600, Entonces lo que queremos encontrar es 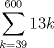$TEX: $$\sum\limits_{k=39}^{600} {13k}$$$ , como 13 es constante, entonces: $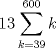TEX: $$13\sum\limits_{k=39}^{600} {k}$$$ Notemos que 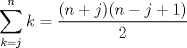$TEX: $$\sum\limits_{k=j}^{n} {k} = \dfrac{(n+j)(n-j+1)}{2}$$$ Por lo que 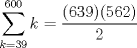$TEX: $$\sum\limits_{k=39}^{600} {k} = \dfrac{(639)(562)}{2}$$$ , Entonces el numero buscado es: $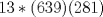TEX: $$13(639)(281)$$$ = $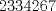TEX: 2334267$