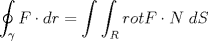|
|
|
|
|
|
|
  |
 Sep 1 2009, 10:26 PM Sep 1 2009, 10:26 PM
Publicado:
#1
|
|
 Dios Matemático Supremo Grupo: Moderador Mensajes: 590 Registrado: 14-October 07 Miembro Nº: 11.310 Colegio/Liceo:  Universidad:  Sexo:  |
Estabamos en prueba de mates, y aparecio este ejercicio, y supuestamente sale con relaciones sencillas de un triangulo rectangulo, pero la solucion que di en la prueba fue tan distinta y tan linda, ademas de solo usar teoria y no calculos directamente, les animo a encontrar mi solucion y que posteen las suyas.
 ss.jpg ( 6.9k )
Número de descargas: 30
ss.jpg ( 6.9k )
Número de descargas: 30Sea AD=h la altura desde A del ABC, y sea BC=2h, ademas sean CD=p y BD=q, demuestre que p=q. Saludos y Dios los bendiga. -------------------- |
|
|
|
 Sep 2 2009, 03:33 PM Sep 2 2009, 03:33 PM
Publicado:
#2
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad:  Colegio/Liceo:  Sexo:  |

Mensaje modificado por Kaissa el Sep 2 2009, 03:35 PM -------------------- |
|
|
|
 Sep 2 2009, 07:45 PM Sep 2 2009, 07:45 PM
Publicado:
#3
|
|
 Dios Matemático Supremo Grupo: Moderador Mensajes: 590 Registrado: 14-October 07 Miembro Nº: 11.310 Colegio/Liceo:  Universidad:  Sexo:  |
 Solucion correcta y parecida a la mia Que Dios los bendiga -------------------- |
|
|
|
 Mar 19 2010, 01:42 PM Mar 19 2010, 01:42 PM
Publicado:
#4
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 688 Registrado: 8-November 09 Desde: Villarrica Miembro Nº: 61.657 Nacionalidad:  Colegio/Liceo:  Universidad: .png) Sexo:  |
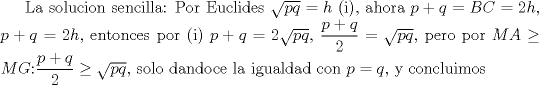
-------------------- yo no soy especial
a pesar que ella lo dijo tengo unos krk y un celular hechizo aún vácilo SFDK en el segundo piso y la frase final da igual la improviso |
|
|
|
 Mar 20 2010, 01:40 PM Mar 20 2010, 01:40 PM
Publicado:
#5
|
|
 Dios Matemático Supremo Grupo: Moderador Mensajes: 590 Registrado: 14-October 07 Miembro Nº: 11.310 Colegio/Liceo:  Universidad:  Sexo:  |
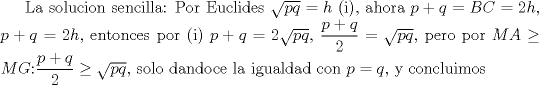 Bonita solución, pero no es la más simple, más simple es la dada por Kaissa, que no recurre más que pura geometría. Saludos. -------------------- |
|
|
|
 Mar 20 2010, 02:17 PM Mar 20 2010, 02:17 PM
Publicado:
#6
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 688 Registrado: 8-November 09 Desde: Villarrica Miembro Nº: 61.657 Nacionalidad:  Colegio/Liceo:  Universidad: .png) Sexo:  |
Bonita solución, pero no es la más simple, más simple es la dada por Kaissa, que no recurre más que pura geometría. Saludos. Con Sencilla me referia a que no hay que realizar contrucciones auxiliares. Se agredece el comentario -------------------- yo no soy especial
a pesar que ella lo dijo tengo unos krk y un celular hechizo aún vácilo SFDK en el segundo piso y la frase final da igual la improviso |
|
|
|
 Jun 17 2013, 04:48 AM Jun 17 2013, 04:48 AM
Publicado:
#7
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.818 Registrado: 3-October 09 Miembro Nº: 59.773 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Mis disculpas por revivir un tema viejo, pero verlo me causó cierta nostalgia y no pude evitar querer sumarme a la causa:
Se traza la mediana 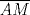 . Es sabido que . Es sabido que 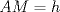 , luego el triángulo , luego el triángulo 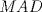 es isósceles de base es isósceles de base 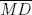 , de lo que se sigue que , de lo que se sigue que 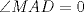 , pues , pues 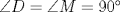 , por lo que , por lo que 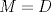 . Finalmente . Finalmente 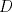 es punto medio, concluyendo que es punto medio, concluyendo que 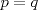  Saludos. -------------------- Me voy, me jui.
|
|
|
|
 Jun 17 2013, 10:40 AM Jun 17 2013, 10:40 AM
Publicado:
#8
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.116 Registrado: 12-March 11 Miembro Nº: 84.732 Nacionalidad:  Sexo:  |
Mis disculpas por revivir un tema viejo, pero verlo me causó cierta nostalgia y no pude evitar querer sumarme a la causa: Se traza la mediana 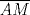 . Es sabido que . Es sabido que 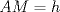 , luego el triángulo , luego el triángulo 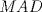 es isósceles de base es isósceles de base 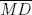 , de lo que se sigue que , de lo que se sigue que 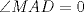 , pues , pues 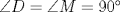 , por lo que , por lo que 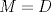 . Finalmente . Finalmente 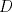 es punto medio, concluyendo que es punto medio, concluyendo que 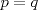  Saludos. Pero ¿por que la mediana=altura, asi de una sin explicacion? si tenes ese dato es entonces inmediato que p=q -------------------- |
|
|
|
 Jun 17 2013, 12:48 PM Jun 17 2013, 12:48 PM
Publicado:
#9
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.818 Registrado: 3-October 09 Miembro Nº: 59.773 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Porque la hipotenusa vale
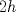 . Y recuerda que la mediana trazada desde el ángulo recto, mide la mitad de ésta. . Y recuerda que la mediana trazada desde el ángulo recto, mide la mitad de ésta.Cev-ludos Mensaje modificado por El Geek el Jun 17 2013, 03:38 PM -------------------- Me voy, me jui.
|
|
|
|
 Oct 12 2013, 11:31 AM Oct 12 2013, 11:31 AM
Publicado:
#10
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad:  Colegio/Liceo:  Sexo:  |
-------------------- |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 6th March 2025 - 09:30 PM |