|
|
|
|
|
|
|
  |
 Aug 8 2009, 08:02 PM Aug 8 2009, 08:02 PM
Publicado:
#1
|
|
 Staff Fmat Grupo: Moderador Mensajes: 1.185 Registrado: 29-October 05 Desde: Santiago, Chile Miembro Nº: 352 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Cuarta Fecha: 8 de Agosto de 2009
1. Si 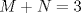 y y 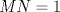 , entonces , entonces 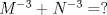 . .2. Dado un conjunto 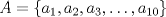 de diez números enteros distintos de diez números enteros distintos 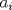 tales que tales que 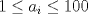 . Pruebe que existen dos subconjuntos disjuntos no vacíos, de . Pruebe que existen dos subconjuntos disjuntos no vacíos, de 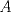 , tales que sus elementos suman lo mismo. , tales que sus elementos suman lo mismo.
-------------------- "He looks rather ill, but he looks all over the genius he was" (G. H. Hardy)
"A mathematician is a device for turning coffee into theorems" (Paul Erdös) |
|
|
|
 Aug 8 2009, 09:37 PM Aug 8 2009, 09:37 PM
Publicado:
#2
|
|
|
Principiante Matemático Grupo: Usuario FMAT Mensajes: 9 Registrado: 30-May 07 Miembro Nº: 6.285 Nacionalidad:  Sexo:  |
|
|
|
|
 Aug 9 2009, 12:41 PM Aug 9 2009, 12:41 PM
Publicado:
#3
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.077 Registrado: 19-December 07 Desde: Santiago, RM. Miembro Nº: 13.971 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
De puro colao xd
![TEX: \[<br />\begin{gathered}<br /> m + n = 3 \hfill \\<br /> m^3 + 3m^2 n + 3mn^2 + n^3 = 3^3 \hfill \\<br /> m^3 + n^3 + 3m^2 n + 3mn^2 = 3^3 \hfill \\<br /> m^3 + n^3 + 3mn(m + n) = 3^3 \hfill \\<br /> m^3 + n^3 + 3 \cdot 1\left( 3 \right) = 3^3 \hfill \\<br /> m^3 + n^3 = 3^3 - 3^2 \hfill \\<br /> m^3 + n^3 = 27 - 9 \hfill \\<br /> \boxed{m^3 + n^3 = 18} \hfill \\<br /> \hfill \\<br /> mn = 1 \hfill \\<br /> \boxed{m^3 n^3 = 1} \hfill \\<br /> \Rightarrow m^{ - 3} + n^{ - 3} = \frac{1}<br />{{m^3 }} + \frac{1}<br />{{n^3 }} = \frac{{n^3 + m^3 }}<br />{{m^3 n^3 }} = \frac{{18}}<br />{1} = \boxed{18} \hfill \\ <br />\end{gathered} <br />\]](./tex/2131ed3436ad8d7f61894269f2bee4cc.png) Saludos Killua |
|
|
|
 Aug 9 2009, 08:30 PM Aug 9 2009, 08:30 PM
Publicado:
#4
|
|
 Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 140 Registrado: 15-May 08 Desde: Rancagua/ Valpo Miembro Nº: 23.226 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
la primera me dio 18 , el lunes o el martes subo el desarrollo q hice como imagen
--------------------      |
|
|
|
 Aug 9 2009, 08:32 PM Aug 9 2009, 08:32 PM
Publicado:
#5
|
|
 Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 140 Registrado: 15-May 08 Desde: Rancagua/ Valpo Miembro Nº: 23.226 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
fue similar al de manuel fco
--------------------      |
|
|
|
 Aug 11 2009, 07:48 PM Aug 11 2009, 07:48 PM
Publicado:
#6
|
|
|
Principiante Matemático Grupo: Usuario FMAT Mensajes: 13 Registrado: 16-July 08 Miembro Nº: 30.099 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
q manera de arrepentirme de no haber dadooo la prueba! >.<
--------------------   |
|
|
|
 Jun 29 2010, 10:11 PM Jun 29 2010, 10:11 PM
Publicado:
#7
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 858 Registrado: 20-August 09 Desde: In my House Miembro Nº: 57.323 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
P2
Notemos que la cantidad de subconjuntos que se pueden hacer de un conjunto de 10 elementos es 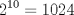 , pero como no consideramos el conjunto vacío, entonces son , pero como no consideramos el conjunto vacío, entonces son 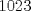 Ahora consideremos los mayores valores posibles de los 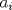 , que sería , que sería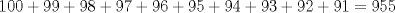 Por lo que la suma máxima es 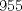 y estas sumas se deben repartir en y estas sumas se deben repartir en 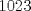 subconjuntos, y por el principio de palomar, va a haber almenos dos subconjuntos que sumen lo mismo. subconjuntos, y por el principio de palomar, va a haber almenos dos subconjuntos que sumen lo mismo. |
|
|
|
 Jul 4 2010, 07:25 PM Jul 4 2010, 07:25 PM
Publicado:
#8
|
|
|
Principiante Matemático Grupo: Usuario FMAT Mensajes: 8 Registrado: 20-April 08 Miembro Nº: 20.615 Nacionalidad:  Colegio/Liceo:  Sexo:  |
casi casi el P2, pero notar que 2 conjuntos cualquiera de los 1023 no necesariamente son disjuntos xD.
Mensaje modificado por apablon el Jul 4 2010, 07:25 PM |
|
|
|
 Jul 4 2010, 09:41 PM Jul 4 2010, 09:41 PM
Publicado:
#9
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 858 Registrado: 20-August 09 Desde: In my House Miembro Nº: 57.323 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
|
|
|
|
 Jul 4 2010, 09:48 PM Jul 4 2010, 09:48 PM
Publicado:
#10
|
|
|
Maestro Matemático Grupo: Usuario FMAT Mensajes: 89 Registrado: 13-May 06 Desde: Santiago, Maipú Miembro Nº: 1.092 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
El enunciado pide que sean disjuntos.
|
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 7th April 2025 - 10:54 AM |












