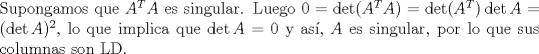|
|
|
|
|
|
|
  |
 Aug 8 2009, 01:29 AM Aug 8 2009, 01:29 AM
Publicado:
#1
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.812 Registrado: 4-November 07 Desde: Santiago Miembro Nº: 12.213 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
-------------------- |
|
|
|
 Aug 22 2009, 03:41 PM Aug 22 2009, 03:41 PM
Publicado:
#2
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.818 Registrado: 21-December 06 Miembro Nº: 3.434 |
Una buena demostración para este problema usa las 2 siguientes desigualdades. (
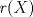 denota al rango de la matriz denota al rango de la matriz 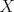 ). ).1) 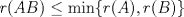 2) 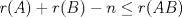 . .Lo pedido se concluye pues si 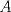 es de es de 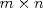 y las columnas de y las columnas de 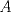 son LI, se sigue que son LI, se sigue que 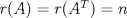 . .Luego, de 1) se tiene 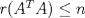 y de 2) se tiene y de 2) se tiene 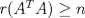 , es decir, , es decir, 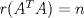 , y como , y como 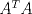 es de es de 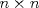 se concluye que es invertible. se concluye que es invertible.
-------------------- |
|
|
|
 Aug 22 2009, 11:31 PM Aug 22 2009, 11:31 PM
Publicado:
#3
|
|
 Staff FMAT Grupo: Super Moderador Mensajes: 4.857 Registrado: 2-January 08 Miembro Nº: 14.268 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Una buena demostración para este problema usa las 2 siguientes desigualdades. ( 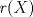 denota al rango de la matriz denota al rango de la matriz 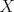 ). ).1) 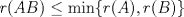 2) 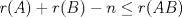 . .Lo pedido se concluye pues si 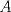 es de es de 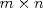 y las columnas de y las columnas de 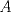 son LI, se sigue que son LI, se sigue que 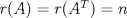 . .Luego, de 1) se tiene 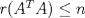 y de 2) se tiene y de 2) se tiene 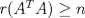 , es decir, , es decir, 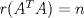 , y como , y como 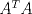 es de es de 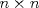 se concluye que es invertible. se concluye que es invertible.Quedo linda la demostración.... Ejercicio robado para la ayudantia xD jajjajaa Saludos -------------------- Candidato a doctor en Cs. De la ingeniería mención modelamiento matemático, DIM. Universidad de Chile
Magíster en ciencias mención matemática, Profesor de estado en matemáticas y computación, Licenciado en educación matemáticas y computación, USACH |
|
|
|
 May 4 2015, 09:02 PM May 4 2015, 09:02 PM
Publicado:
#4
|
|
 Dios Matemático Supremo Grupo: Super Moderador Mensajes: 1.912 Registrado: 10-January 08 Desde: Un Sobolev Miembro Nº: 14.530 Nacionalidad:  Sexo:  |
Otra forma, probando el contrarrecíproco.

-------------------- |
|
|
|
 May 5 2015, 01:02 PM May 5 2015, 01:02 PM
Publicado:
#5
|
|
|
Principiante Matemático Grupo: Usuario FMAT Mensajes: 5 Registrado: 5-May 15 Miembro Nº: 137.512 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Columnas de A L.I <=> rango(A)=n <=> A es sobreyectiva <=> A es invertible <=> A^t es invertible => (A^t)A es invertible
|
|
|
|
 May 5 2015, 03:06 PM May 5 2015, 03:06 PM
Publicado:
#6
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 465 Registrado: 15-July 11 Miembro Nº: 91.905 Nacionalidad:  Universidad:  Sexo:  |
Columnas de A L.I <=> rango(A)=n <=> A es sobreyectiva <=> A es invertible <=> A^t es invertible => (A^t)A es invertible Si y solo si? -------------------- He-llo? Could you say that again? More slowly? In a language I understand? Depending on what you said, I might kick your ass! |
|
|
|
 May 5 2015, 03:44 PM May 5 2015, 03:44 PM
Publicado:
#7
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 832 Registrado: 11-September 07 Desde: París, Francia Miembro Nº: 10.056 Nacionalidad:  Sexo:  |
|
|
|
|
 May 5 2015, 07:38 PM May 5 2015, 07:38 PM
Publicado:
#8
|
|
 Dios Matemático Supremo Grupo: Super Moderador Mensajes: 1.912 Registrado: 10-January 08 Desde: Un Sobolev Miembro Nº: 14.530 Nacionalidad:  Sexo:  |
Como defines el determinante de una matriz no cuadrada? Edité el post (no había leído que no necesariamente A era cuadrada) 
-------------------- |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 8th July 2025 - 12:52 AM |






![TEX: \[\mathfrak{L}=\int_{-\infty}^\infty e^{-289x^2}dx=\frac{\Gamma (\frac{1}{2})}{17}=\frac{\sqrt{\pi}}{17}\]](./tex/e0e88dba678ca3ead120b088f41191b2.png)