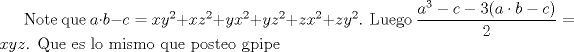1º Maraton Olimpica 2009

Foro fmat.cl > Sector Preparación Olimpiadas > Competencias Olimpicas FMAT

19 Páginas:

« < 5 6 7 8 9 > »

1º Maraton Olimpica 2009, Lectura Obligatoria

Opciones

Newtype Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 4 2009, 09:22 PM Publicado: #61
Dios Matemático Supremo Grupo: Team Ensayos FMAT Mensajes: 1.559 Registrado: 18-November 07 Miembro Nº: 12.754 Nacionalidad: Sexo:	muy buena, taba en las mismas pero haciendolo en una hoja quizas pa sacar mas rapidez sirva hacerlo directo en pc XD -------------------- Empezando con Desigualdades? Encuentra aquí problemas resueltos

ojotas Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 4 2009, 09:22 PM Publicado: #62
Dios Matemático Grupo: Usuario FMAT Mensajes: 262 Registrado: 12-July 09 Desde: mi ksa Miembro Nº: 55.521 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	geometria analitica porfaaa -------------------- PONGAN AL COLEGIO CORDILLERA DE LAS CCONDES PARA REGISTRARSE

makmat Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 4 2009, 09:30 PM Publicado: #63
Dios Matemático Supremo Grupo: Moderador Mensajes: 590 Registrado: 14-October 07 Miembro Nº: 11.310 Colegio/Liceo: Universidad: Sexo:	otra $TEX: Note que $a\cdot b-c=xy^2+xz^2+yx^2+yz^2+zx^2+zy^2$. Luego $\dfrac {a^3-c-3(a\cdot b -c)}{2}=xyz$. Que es lo mismo que posteo gpipe$ Felicitaciones gpipe La Gloria sea al Señor. Muy relindos los problemas. Mensaje modificado por makmat el Aug 4 2009, 09:31 PM -------------------- $TEX: $displaystyle oint _{gamma} F cdot dr = displaystyle int int_{R} (dfrac{partial N}{partial x} - dfrac{partial M}{partial y}) dA$$ $TEX: $frac{a+b}{2}ge sqrt{ab}$$ [!] $TEX: $displaystyle int_{Mak^2}^{Mat}Mak^{Mat^{Mak}_{Mat}}dx$$ Doctor en Matemáticas Estudiando y creando problemas $TEX: MakMat$ $TEX: $displaystyle oint_{gamma} F cdot dr= int int_{R} rot F cdot black{N} dS$$ Adiós Kazajstán...

~Fatal_Collapse~ Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 4 2009, 09:55 PM Publicado: #64
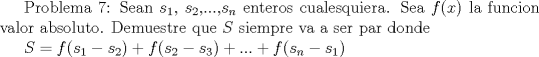
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.564 Registrado: 12-November 07 Desde: La Union, XIV Region de los Rios Miembro Nº: 12.607 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Sigamos: $TEX: Problema 7: Sean $s_{1}$, $s_{2}$,...,$s_n$ enteros cualesquiera. Sea $f(x)$ la funcion valor absoluto. Demuestre que $S$ siempre va a ser par donde<br /><br />$S=f(s_1-s_2)+f(s_2-s_3)+...+f(s_n-s_1)$$ -------------------- Ricardo Vargas Obando Ex-alumno Deutsche Schule La Unión (Generación 2010, de los 150 años). Novato de Licenciatura en Matemática/Estadística, en la Pontificia Universidad Católica de Chile. Grupo de facebook de Novatos Matemática y Estadística PUC 2011 Currículum Olímpico: Medalla de Plata, XIX Olimpiada Nacional de Matemática Nivel Menor (2007) Medalla de Oro, XXI Olimpiada Nacional de Matemática Nivel Mayor (2009) Medalla de Bronce, XXV Olimpiada Iberoamericana de Matemática (2010) Medalla de Oro, XXII Olimpiada Nacional de Matemática Nivel Mayor (2010) "What we learned as children, that one plus one equals two, we know to be false. One plus one equals one. We even have a word when you plus another, equals one. That word is love." "Todos piensan en cambiar el mundo, pero nadie piensa en cambiarse a sí mismo."

gpipe Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 4 2009, 10:01 PM Publicado: #65
Matemático Grupo: Usuario FMAT Mensajes: 36 Registrado: 18-August 07 Miembro Nº: 8.943 Nacionalidad: Sexo:	$TEX: Usare congruencia modulo 2 (todo sera en esta congruencia (0,1)), notemos que $f(x) \equiv x$(basta probar con los posibles restos) luego $S\equiv (s_1-s_2)+(s_2-s_3)+...+(s_n-s_1)\equiv0$ luego $S$ es par$ EDITADO Mensaje modificado por gpipe el Aug 4 2009, 10:06 PM

ojotas Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 4 2009, 10:03 PM Publicado: #66
Dios Matemático Grupo: Usuario FMAT Mensajes: 262 Registrado: 12-July 09 Desde: mi ksa Miembro Nº: 55.521 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	una pregunta los s pertenecen a la funcion? -------------------- PONGAN AL COLEGIO CORDILLERA DE LAS CCONDES PARA REGISTRARSE

Newtype Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 4 2009, 10:03 PM Publicado: #67
Dios Matemático Supremo Grupo: Team Ensayos FMAT Mensajes: 1.559 Registrado: 18-November 07 Miembro Nº: 12.754 Nacionalidad: Sexo:	breve y claro PD: debes ponerle Spoiler -------------------- Empezando con Desigualdades? Encuentra aquí problemas resueltos

ojotas Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 4 2009, 10:07 PM Publicado: #68
Dios Matemático Grupo: Usuario FMAT Mensajes: 262 Registrado: 12-July 09 Desde: mi ksa Miembro Nº: 55.521 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: Teniendo la Funcion valor absoluto, y los S pertenecientes a ella se obtendra por simple inspeccion de la funcion una suma de numeros la cual dará positivo, es decir si se tiene la funcion y=valor absoluto de x se puede tomar un valor cualquiera restarle el vertice, y al sumarlo con los demas dará par comprobable por simple inspeccion$ -------------------- PONGAN AL COLEGIO CORDILLERA DE LAS CCONDES PARA REGISTRARSE

makmat Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 4 2009, 10:07 PM Publicado: #69
Dios Matemático Supremo Grupo: Moderador Mensajes: 590 Registrado: 14-October 07 Miembro Nº: 11.310 Colegio/Liceo: Universidad: Sexo:	$TEX: Considere que independiente de si $s_i-s_{i+1}$ el resultado o es par o es impar, luego basta probar que se obitene de operar $(s_1-s_2)+...+(s_n+s_1)$ si es que el resultado será par o impar, como $(s_1-s_2)+...+(s_n+s_1)=0$, independiente del signo la expresión del enunciado siempre será par.$ Me ganó gpipe (cabro seco), bendiciones Y que la paz del Señor esté con ustedes. -------------------- $TEX: $displaystyle oint _{gamma} F cdot dr = displaystyle int int_{R} (dfrac{partial N}{partial x} - dfrac{partial M}{partial y}) dA$$ $TEX: $frac{a+b}{2}ge sqrt{ab}$$ [!] $TEX: $displaystyle int_{Mak^2}^{Mat}Mak^{Mat^{Mak}_{Mat}}dx$$ Doctor en Matemáticas Estudiando y creando problemas $TEX: MakMat$ $TEX: $displaystyle oint_{gamma} F cdot dr= int int_{R} rot F cdot black{N} dS$$ Adiós Kazajstán...

~Fatal_Collapse~ Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 4 2009, 10:08 PM Publicado: #70
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.564 Registrado: 12-November 07 Desde: La Union, XIV Region de los Rios Miembro Nº: 12.607 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Solucion correcta de gpipe Probablemente a cualquiera que no haya estudiado congruencia modulo (estudienta chiquillos, sirve caleta) la solucion de gpipe le parecera escrita en chino mandarin Miren, diremos que $TEX: $a$$ es congruente a 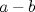$TEX: $b$$ modulo $TEX: $n$$ si $TEX: $n$$ divide a la diferencia $TEX: $a-b$$ Ahora, considerando modulo dos es PARIDAD!!!!! (les dije que servia xD). Eso, saludos PD: ojotas, $f(x)$ esta definidas pa los reales (valor absoluto), asi que los $s_i$ estaban bien definidas -------------------- Ricardo Vargas Obando Ex-alumno Deutsche Schule La Unión (Generación 2010, de los 150 años). Novato de Licenciatura en Matemática/Estadística, en la Pontificia Universidad Católica de Chile. Grupo de facebook de Novatos Matemática y Estadística PUC 2011 Currículum Olímpico: Medalla de Plata, XIX Olimpiada Nacional de Matemática Nivel Menor (2007) Medalla de Oro, XXI Olimpiada Nacional de Matemática Nivel Mayor (2009) Medalla de Bronce, XXV Olimpiada Iberoamericana de Matemática (2010) Medalla de Oro, XXII Olimpiada Nacional de Matemática Nivel Mayor (2010) "What we learned as children, that one plus one equals two, we know to be false. One plus one equals one. We even have a word when you plus another, equals one. That word is love." "Todos piensan en cambiar el mundo, pero nadie piensa en cambiarse a sí mismo."

« Posterior · Competencias Olimpicas FMAT · Anterior »

19 Páginas:

« < 5 6 7 8 9 > »

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 22nd December 2024 - 03:42 AM