|
|
|
|
|
|
|
  |
 Feb 7 2007, 04:09 PM Feb 7 2007, 04:09 PM
Publicado:
#11
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 765 Registrado: 6-December 05 Miembro Nº: 458 Nacionalidad:  Sexo:  |
Respuesta correcta de Felip.
Para dejarlo mas claro, basta elegir un punto cualquiera de la rivera distinto del que suponemos optimo y ver que pasa, considerando que la distancia mas corta entre dos puntos (en geometria Euclideana) es una linea recta y cualquier otra trayectoria es mas larga (o usar la desigualdad triangular). Recordemos que el sector es para los que comienzan asi que para los personajes ya conocidos del foro y con experiencia; dejemos los problemas a los que se inician. Saludos -------------------- Pasten, un buen muchacho en quien confiar.
|
|
|
|
 Feb 19 2007, 11:57 AM Feb 19 2007, 11:57 AM
Publicado:
#12
|
|
|
Dios Matemático Supremo Grupo: Baneado Mensajes: 2.588 Registrado: 7-November 06 Miembro Nº: 2.747 |
CITA(sebagarage @ Feb 3 2007, 04:15 PM) Respuesta correcta, pero con falta de argumento, pues falta mostrar que el trayecto 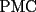 es efectivamente el más corto, esto es, que para cualquier punto es efectivamente el más corto, esto es, que para cualquier punto 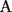 sobre el río, el trayecto sobre el río, el trayecto 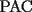 es mayor que el es mayor que el 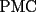 , algo que tal vez no sea muy complicado, pero que es fundamental en una solución formal al problema. , algo que tal vez no sea muy complicado, pero que es fundamental en una solución formal al problema.si se escoge otro camino aun punto P perteneciente al rio (que no sea M) y luego se dirige hacia la casa, tambien "podemos reflejar" ese camino al reflejo de C, y se formaria un triangulo, y los caminos "reflejo" son iguales a los caminos "reales". Por la desigualdad triangular sabemos que un lado es menor que la suma de los otros dos, por lo tanto el camino PMC es mas corto que cualquier otro camino posible. |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 8th July 2025 - 12:56 AM |










