|
|
|
|
|
|
|
  |
 Oct 20 2006, 11:23 AM Oct 20 2006, 11:23 AM
Publicado:
#1
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 765 Registrado: 6-December 05 Miembro Nº: 458 Nacionalidad:  Sexo:  |
 screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img244.imageshack.us/img244/6655/riopk1.png');}" /> screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img244.imageshack.us/img244/6655/riopk1.png');}" />Segun se ve en la imagen, una persona esta ubicada en el punto rojo y su casa en el punto azul. Esta persona debe ir a su casa, pero antes debe pasar a buscar agua al rio. Es decir, debe ir a su casa pasando por el rio. Dibujar justificadamente que camino debe seguir la persona para caminar lo menos posible. Saludos -------------------- Pasten, un buen muchacho en quien confiar.
|
|
|
|
 Jan 21 2007, 05:05 PM Jan 21 2007, 05:05 PM
Publicado:
#2
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 836 Registrado: 9-January 07 Desde: Santiasko Miembro Nº: 3.659 Nacionalidad:  Sexo:  |
Disculpar por favor...
Editado Mensaje modificado por Felipe_ambuli el Feb 19 2007, 06:26 PM |
|
|
|
 Jan 24 2007, 09:49 PM Jan 24 2007, 09:49 PM
Publicado:
#3
|
|
 Dios Matemático Supremo Grupo: Colaborador Silver Mensajes: 817 Registrado: 28-May 06 Desde: maipú, santiago. Miembro Nº: 1.210 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
CITA Bueno supongo que la menor distancia es en linea recta,desde la persona al rio se debe dibujar una linea que sea perpendicular al rio y luego regresar a casa tambien en linea recta. Respuesta incorrecta. De hecho, deberías tratar de dar algún argumento convincente de lo que afirmas, no sólo "suponer". Saludos. -------------------- Estudiante de 5º año de Ingeniería Civil Industrial en la U. de Chile
|
|
|
|
 Jan 25 2007, 12:02 AM Jan 25 2007, 12:02 AM
Publicado:
#4
|
|
|
Dios Matemático Supremo Grupo: Baneado Mensajes: 2.588 Registrado: 7-November 06 Miembro Nº: 2.747 |
geodesicas
|
|
|
|
 Jan 25 2007, 09:42 AM Jan 25 2007, 09:42 AM
Publicado:
#5
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
El problema debe ser resuelto con geometría euclidiana, nada más allá de lo que se aprende en el colegio. No es necesario saber de geodésicas para este problema (de hecho, qué es una geodésica en este caso?). Piensa que la persona quiere que le digan: camina de esta manera... y no sabe qué es una geodésica.
Observen que las riberas del río son rectas, eso es necesario para resolver el problema -------------------- |
|
|
|
 Jan 25 2007, 12:35 PM Jan 25 2007, 12:35 PM
Publicado:
#6
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 836 Registrado: 9-January 07 Desde: Santiasko Miembro Nº: 3.659 Nacionalidad:  Sexo:  |
Editado
Mensaje modificado por Felipe_ambuli el Feb 19 2007, 06:18 PM |
|
|
|
 Jan 25 2007, 09:25 PM Jan 25 2007, 09:25 PM
Publicado:
#7
|
|
 Dios Matemático Supremo Grupo: Colaborador Silver Mensajes: 817 Registrado: 28-May 06 Desde: maipú, santiago. Miembro Nº: 1.210 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
CITA 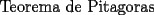 screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://www.fmat.cl/tex/1169746615.gif');}" /> screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://www.fmat.cl/tex/1169746615.gif');}" />Sin intención de ser pesado, tu post no tiene ningún aporte al problema. Como hint puedo decirte que no es necesario el teorema de Pitágoras. Saludos. -------------------- Estudiante de 5º año de Ingeniería Civil Industrial en la U. de Chile
|
|
|
|
 Feb 3 2007, 01:27 PM Feb 3 2007, 01:27 PM
Publicado:
#8
|
|
 Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 166 Registrado: 15-October 06 Desde: desde mi compu en temuco Miembro Nº: 2.532 Nacionalidad:  Universidad:  Sexo:  |
 revisando unos apuntes se me ocurrio gacer una acotacion se puede hacer una refleccion en torna al rio para que asi la persona un la casa queden un una recta colinal la cual seria la mas corta? eso es como una pregunta acotacion sin muxo fundamento y harto jugo pero = se podria aclara mi duda ok [jugo]esto lo que acabo de decir fu una duda que no se se supo redactar bien porfa respondanla plis help[jugo\] --------------------  weno El hombre que en los mas hondo de su ser, duda de sí mismo, jamás encontrará quien lo acompañe [H. Keyserling.] Allí donde se hicieorn los caminos, o he perdido el mio.(XxryurickxX) Defiende tu derecho a pensar, porque incluso pensar en forma errónea es mejor que no pensar (Hipatia) Si buscas resultados distintos, no hagas siempre lo mismo (Albert Einstein) |
|
|
|
 Feb 3 2007, 02:05 PM Feb 3 2007, 02:05 PM
Publicado:
#9
|
|
 Dios Matemático Supremo Grupo: Colaborador Gold Mensajes: 1.374 Registrado: 22-July 06 Desde: San Ramon Miembro Nº: 1.746 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
 screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img251.imageshack.us/img251/4569/riooa6.png');}" /> screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img251.imageshack.us/img251/4569/riooa6.png');}" />Hacemos primero una simetria axial de la casa © con respecto al río y obtenemos C*. Luego trazamos una recta entre P y C*, que es la distancia mas corta entre estos dos puntos. Pero como MC=MC* por ser lados homólogos de triangulos congruentes. Y tenemos Nuestro trayecto PMC. -------------------- Segundo en olimpíadas de Física Región Metropolitana Nivel Tercero Medio, 2006.
Cuarto en olimpíadas de Física Región Metropolitana Nivel Cuarto Medio, 2007. Mejor egresado Instituto Nacional generación 2007 Puntaje Nacional en PSU de Matemáticas 2007, con 850 puntos. Mejor egresado de Ingeniería Civil PUC 2014, con promedio 6,6. |
|
|
|
 Feb 3 2007, 03:15 PM Feb 3 2007, 03:15 PM
Publicado:
#10
|
|
 Dios Matemático Supremo Grupo: Colaborador Silver Mensajes: 817 Registrado: 28-May 06 Desde: maipú, santiago. Miembro Nº: 1.210 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
CITA(Felip @ Feb 3 2007, 04:05 PM)  screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img251.imageshack.us/img251/4569/riooa6.png');}" /> screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img251.imageshack.us/img251/4569/riooa6.png');}" />Hacemos primero una simetria axial de la casa © con respecto al río y obtenemos C*. Luego trazamos una recta entre P y C*, que es la distancia mas corta entre estos dos puntos. Pero como MC=MC* por ser lados homólogos de triangulos congruentes. Y tenemos Nuestro trayecto PMC. Respuesta correcta, pero con falta de argumento, pues falta mostrar que el trayecto 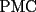 es efectivamente el más corto, esto es, que para cualquier punto es efectivamente el más corto, esto es, que para cualquier punto 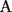 sobre el río, el trayecto sobre el río, el trayecto 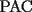 es mayor que el es mayor que el 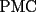 , algo que tal vez no sea muy complicado, pero que es fundamental en una solución formal al problema. , algo que tal vez no sea muy complicado, pero que es fundamental en una solución formal al problema.
-------------------- Estudiante de 5º año de Ingeniería Civil Industrial en la U. de Chile
|
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 3rd April 2025 - 11:05 PM |










