Lim en varias - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Programa Enseñanza Universitaria > Consultas > Banco de Problemas Resueltos > Cálculo > Cálculo en Varias Variables

2 Páginas:

1 2 >

Reply to this topic

Start new topic

Lim en varias

Darr3n Ver Perfil del Miembro Ver los mensajes de este miembro	Jun 14 2009, 07:25 PM Publicado: #1
Dios Matemático Grupo: Usuario FMAT Mensajes: 204 Registrado: 22-January 08 Desde: Est. Central Miembro Nº: 14.887 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Cual es el truquillo para este ?? $TEX: % MathType!MTEF!2!1!+-<br />% feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaacaqGeb<br />% GaaeyzaiaabshacaqGLbGaaeOCaiaab2gacaqGPbGaaeOBaiaabgga<br />% caqGYbGaaeiiaiaabYgacaqGHbGaaeiiaiaabwgacaqG4bGaaeyAai<br />% aabohacaqG0bGaaeyzaiaab6gacaqGJbGaaeyAaiaabggacaqGGaGa<br />% aeizaiaabwgacaqGSbGaaeiiaiaabYgacaqGTdGaaeyBaiaabMgaca<br />% qG0bGaaeyzaiaabQdaaeaadaWfqaqaaiGacYgacaGGPbGaaiyBaaWc<br />% baGaaiikaiaadIhacaGGSaGaamyEaiaacMcacqGHsgIRcaGGOaGaaG<br />% imaiaacYcacaaIWaGaaiykaaqabaGcdaWcaaqaaiaadIhacaWG5baa<br />% baWaaOaaaeaacaWG4bWaaWbaaSqabeaacaaIYaaaaOGaey4kaSIaam<br />% yEamaaCaaaleqabaGaaGOmaaaaaeqaaaaaaaaa!69B1!<br />\[<br />\begin{gathered}<br /> {\text{Determinar la existencia del l\'imite:}} \hfill \\<br /> \mathop {\lim }\limits_{(x,y) \to (0,0)} \frac{{xy}}<br />{{\sqrt {x^2 + y^4 } }} \hfill \\ <br />\end{gathered} <br />\]<br />$ --------------------

xdanielx Ver Perfil del Miembro Ver los mensajes de este miembro	Jun 14 2009, 07:56 PM Publicado: #2
Dios Matemático Supremo Grupo: Baneado Mensajes: 3.360 Registrado: 11-March 08 Miembro Nº: 16.617	Lo he hecho de muchas formas y llego a 0 si nos acercamos al origen mediante la recta 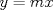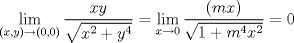$TEX: $y = mx$$ $TEX: $$<br />\mathop {\lim }\limits_{\left( {x,y} \right) \to \left( {0,0} \right)} \frac{{xy}}<br />{{\sqrt {x^2 + y^4 } }} = \mathop {\lim }\limits_{x \to 0} \frac{{\left( {mx} \right)}}<br />{{\sqrt {1 + m^4 x^2 } }} = 0<br />$$$ pero esto no nos asegura que el limite sea 0 ya que en otras direcciones puede tener otro valor si nos acercamos al origen mediante la curva 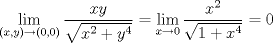$TEX: $y = x^2$$ $TEX: $$<br />\mathop {\lim }\limits_{\left( {x,y} \right) \to \left( {0,0} \right)} \frac{{xy}}<br />{{\sqrt {x^2 + y^4 } }} = \mathop {\lim }\limits_{x \to 0} \frac{{x^2 }}<br />{{\sqrt {1 + x^4 } }} = 0<br />$$$ entonces el limite es cero nota lo sig 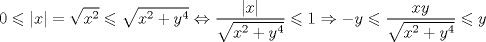$TEX: $$<br />0 \leqslant \left\| x \right\| = \sqrt {x^2 } \leqslant \sqrt {x^2 + y^4 } \Leftrightarrow \frac{{\left\| x \right\|}}<br />{{\sqrt {x^2 + y^4 } }} \leqslant 1 \Rightarrow - y \leqslant \frac{{xy}}<br />{{\sqrt {x^2 + y^4 } }} \leqslant y<br />$$$ acotando, por teorema del encaje 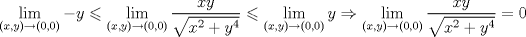$TEX: $$<br />\mathop {\lim }\limits_{\left( {x,y} \right) \to \left( {0,0} \right)} - y \leqslant \mathop {\lim }\limits_{\left( {x,y} \right) \to \left( {0,0} \right)} \frac{{xy}}<br />{{\sqrt {x^2 + y^4 } }} \leqslant \mathop {\lim }\limits_{\left( {x,y} \right) \to \left( {0,0} \right)} y \Rightarrow \mathop {\lim }\limits_{\left( {x,y} \right) \to \left( {0,0} \right)} \frac{{xy}}<br />{{\sqrt {x^2 + y^4 } }} = 0<br />$$$ Mensaje modificado por xdanielx el Jun 14 2009, 08:24 PM

Abu-Khalil Ver Perfil del Miembro Ver los mensajes de este miembro	Jun 14 2009, 08:46 PM Publicado: #3
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.812 Registrado: 4-November 07 Desde: Santiago Miembro Nº: 12.213 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(xdanielx @ Jun 14 2009, 08:47 PM) Lo he hecho de muchas formas y llego a 0 si nos acercamos al origen mediante la recta 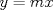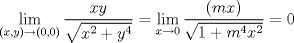$TEX: $y = mx$$ $TEX: $$<br />\mathop {\lim }\limits_{\left( {x,y} \right) \to \left( {0,0} \right)} \frac{{xy}}<br />{{\sqrt {x^2 + y^4 } }} = \mathop {\lim }\limits_{x \to 0} \frac{{\left( {mx} \right)}}<br />{{\sqrt {1 + m^4 x^2 } }} = 0<br />$$$ pero esto no nos asegura que el limite sea 0 ya que en otras direcciones puede tener otro valor si nos acercamos al origen mediante la curva 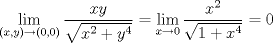$TEX: $y = x^2$$ $TEX: $$<br />\mathop {\lim }\limits_{\left( {x,y} \right) \to \left( {0,0} \right)} \frac{{xy}}<br />{{\sqrt {x^2 + y^4 } }} = \mathop {\lim }\limits_{x \to 0} \frac{{x^2 }}<br />{{\sqrt {1 + x^4 } }} = 0<br />$$$ entonces el limite es cero Ojo que tomar dos caminos distintos y llegar a lo mismo no implica nada. Aplica polares y mira que $TEX: \[\lim_{(x,y)\to(0,0)}\frac{xy}{\sqrt{x^2+y^4}}=\lim_{r\to 0}\frac{r^2\sin\theta\cos\theta}{\sqrt{r^2\cos^2\theta+r^4\sin^4\theta}}=\lim_{r\to 0}\frac{r\cos\theta\sin\theta}{\sqrt{\cos^2\theta+r^2\sin^4\theta}}=0.\]$ -------------------- ~milopez $TEX: \[\mathfrak{L}=\int_{-\infty}^\infty e^{-289x^2}dx=\frac{\Gamma (\frac{1}{2})}{17}=\frac{\sqrt{\pi}}{17}\]$ $TEX: <br />\begin{equation}\begin{aligned}<br />dS_t&=\mu S_t dt+\sqrt{V_t}S_t dW^S_t\\<br />dV_t&=\kappa(\theta-V_t)dt+\sigma\sqrt{V_t} dW^V_t\\<br />\end{aligned}\end{equation}<br />$ $TEX: <br />$$\mathbb A^{\text U}_M(N)$$<br />$

Darr3n Ver Perfil del Miembro Ver los mensajes de este miembro	Jun 14 2009, 10:38 PM Publicado: #4
Dios Matemático Grupo: Usuario FMAT Mensajes: 204 Registrado: 22-January 08 Desde: Est. Central Miembro Nº: 14.887 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(Abu-Khalil @ Jun 14 2009, 09:46 PM) Ojo que tomar dos caminos distintos y llegar a lo mismo no implica nada. Aplica polares y mira que $TEX: \[\lim_{(x,y)\to(0,0)}\frac{xy}{\sqrt{x^2+y^4}}=\lim_{r\to 0}\frac{r^2\sin\theta\cos\theta}{\sqrt{r^2\cos^2\theta+r^4\sin^4\theta}}=\lim_{r\to 0}\frac{r\cos\theta\sin\theta}{\sqrt{\cos^2\theta+r^2\sin^4\theta}}=0.\]$ Gracias compa yo apliqué coordenadas polares en este límite, usando trayectorias no pude concluir nada,clarísimo . Gracias . --------------------

VivianaCM Ver Perfil del Miembro Ver los mensajes de este miembro	Jun 25 2010, 09:37 PM Publicado: #5
Principiante Matemático Grupo: Usuario FMAT Mensajes: 14 Registrado: 31-January 07 Miembro Nº: 3.923 Nacionalidad: Sexo:	CITA(Darr3n @ Jun 14 2009, 11:38 PM) Gracias compa yo apliqué coordenadas polares en este límite, usando trayectorias no pude concluir nada,clarísimo . Gracias . Entonces cuando pruebo con Polares puedo estar 100% segura?

Kura Ver Perfil del Miembro Ver los mensajes de este miembro	Jun 25 2010, 09:47 PM Publicado: #6
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.918 Registrado: 14-May 08 Desde: The Tower of God Miembro Nº: 23.100 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(VivianaCM @ Jun 25 2010, 09:37 PM) Entonces cuando pruebo con Polares puedo estar 100% segura? Si, pero siempre y cuando puedas concluir algo por polares. -------------------- Far over... the misty mountains cold. To dungeons deep and caverns old. We must away ere break of day. To find our long-forgotten gold. The pines were roaring on the height. The winds were moaning in the night. The fire was red, it flaming spread. The trees like torches blazed with light. Apunte: Sistemas de Ecuaciones Cuadráticas! Apunte: Series de Fourier! Problemas Resueltos: EDO! OMG! Soy el ñoño de eléctrica.

mikel ramone Ver Perfil del Miembro Ver los mensajes de este miembro	Jun 25 2010, 09:57 PM Publicado: #7
Dios Matemático Grupo: Usuario FMAT Mensajes: 363 Registrado: 27-September 09 Desde: Desde el más arido rock!!! :D Miembro Nº: 59.392 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(VivianaCM @ Jun 25 2010, 10:37 PM) Entonces cuando pruebo con Polares puedo estar 100% segura? http://www.fmat.cl/index.php?showtopic=578...mp;#entry432963 Chequea ese ejercicio te puede servir ... -------------------- Tampoco entendemos si no es. $TEX: $$\underset{\varepsilon \to 0}{\mathop{\lim }}\,\frac{\varepsilon }{\text{ }\varepsilon ^{2}}=\infty$$$ El 98% de los adolescentes han fumado, si eres del dichoso 2% que no lo ha hecho, copia y pega esto en tu firma

Deac Ver Perfil del Miembro Ver los mensajes de este miembro	Mar 16 2013, 05:31 PM Publicado: #8
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.262 Registrado: 29-May 10 Desde: Arica Miembro Nº: 71.591 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Una consulta, estaba buscando ejercicios de limites y me encontré con este tema. Pude calcular este límite perfectamente por definición, sandwich, etc. Mi duda radica con polares en este ejercicio. 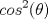En este caso en particular, ¿qué sucede si cuando $TEX: $$r$$$ está tendiendo a cero justo existe un angulo en que $TEX: $$cos^2(\theta)$$$ se hace cero? ¿No existiría un posibilidad que el denominador fuera más rápido? Siempre en esto casos en que con polares puede dar cero en el denominador me da mala espina xd le doy el quite atacando por otro método xd -------------------- Estudiante de Ingeniería Civil Industrial, Diploma en Ingeniería Eléctrica. Áreas de Especialización e Interés: Potencias y Energía. "Y para mí, las cosas más bellas del universo son las más misteriosas" -Albert Einstein Frases Célebres Notable comentario de snw a un usuario puc xD: CITA(snw @ Jan 15 2012, 01:53 PM) oye para de hablar leseras porfa. Andate a rezar mejor CITA(GoChuck @ Jan 4 2012, 07:12 PM) it's free+minas ricas+wena educación= teta CITA(YaRly @ Jan 4 2012, 05:51 PM) La otra vez en 9GAG leí esto: "Cuando tengas que tomar una decisión difícil, tira una moneda. Mientras la moneda esté en el aire, sabrás qué es lo que realmente quieres" Es 9GAG, pero la afirmación tiene sentido. Probablemente ahí empezarás a hinchar por alguna de las dos opciones... Mensaje de motivación xD: CITA(destroyer @ May 20 2012, 05:52 PM) Recuerdo cuando llegue y era un penca igual que tú... pero aquí te enderezaremos a palos :) . Bienvenido! CITA(Can9ri @ Jun 23 2012, 01:17 AM) Para que queremos buenos puntajes si entra gente así a la universidad? ajajajaj Pendejos, pendejos everywhere ... PD: Edúquese lo más que pueda, respete para que lo respeten (: CITA(MatematicoPrincipiante @ Jul 17 2012, 06:18 PM) lamentablemente no alcancé a leer eso de lo que hablan, pero en verdad creo que es mejor así, no importa cual sea la identidad de kaissa...estamos en un foro de matemáticas, no en facebook, importa un pico si kaissa es hombre, mujer, buena para culear, etc., mientras sea una buena usuaria, que aporte frecuentemente lo demás pasa a segundo plano, es más ni siquiera deberia ser tema. Deberían bajar del olimpo en el que se encuentran y dedicarse a aportar, porque ser el matemático del foro vale callampa si no se transmite el conocimiento a los demás...pero en fin no importa la opinión de un simple mortal, que jamás alcanzara el olimpo CITA(Kaissa @ Jun 26 2012, 09:24 PM) saberse el nombre del truco es 0.5% de lo importante, lo realmente poderoso es saberlo usar en batalla y ESO sólo te lo dice la experiencia personal.

Deac Ver Perfil del Miembro Ver los mensajes de este miembro	Mar 17 2013, 11:45 AM Publicado: #9
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.262 Registrado: 29-May 10 Desde: Arica Miembro Nº: 71.591 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	UP! -------------------- Estudiante de Ingeniería Civil Industrial, Diploma en Ingeniería Eléctrica. Áreas de Especialización e Interés: Potencias y Energía. "Y para mí, las cosas más bellas del universo son las más misteriosas" -Albert Einstein Frases Célebres Notable comentario de snw a un usuario puc xD: CITA(snw @ Jan 15 2012, 01:53 PM) oye para de hablar leseras porfa. Andate a rezar mejor CITA(GoChuck @ Jan 4 2012, 07:12 PM) it's free+minas ricas+wena educación= teta CITA(YaRly @ Jan 4 2012, 05:51 PM) La otra vez en 9GAG leí esto: "Cuando tengas que tomar una decisión difícil, tira una moneda. Mientras la moneda esté en el aire, sabrás qué es lo que realmente quieres" Es 9GAG, pero la afirmación tiene sentido. Probablemente ahí empezarás a hinchar por alguna de las dos opciones... Mensaje de motivación xD: CITA(destroyer @ May 20 2012, 05:52 PM) Recuerdo cuando llegue y era un penca igual que tú... pero aquí te enderezaremos a palos :) . Bienvenido! CITA(Can9ri @ Jun 23 2012, 01:17 AM) Para que queremos buenos puntajes si entra gente así a la universidad? ajajajaj Pendejos, pendejos everywhere ... PD: Edúquese lo más que pueda, respete para que lo respeten (: CITA(MatematicoPrincipiante @ Jul 17 2012, 06:18 PM) lamentablemente no alcancé a leer eso de lo que hablan, pero en verdad creo que es mejor así, no importa cual sea la identidad de kaissa...estamos en un foro de matemáticas, no en facebook, importa un pico si kaissa es hombre, mujer, buena para culear, etc., mientras sea una buena usuaria, que aporte frecuentemente lo demás pasa a segundo plano, es más ni siquiera deberia ser tema. Deberían bajar del olimpo en el que se encuentran y dedicarse a aportar, porque ser el matemático del foro vale callampa si no se transmite el conocimiento a los demás...pero en fin no importa la opinión de un simple mortal, que jamás alcanzara el olimpo CITA(Kaissa @ Jun 26 2012, 09:24 PM) saberse el nombre del truco es 0.5% de lo importante, lo realmente poderoso es saberlo usar en batalla y ESO sólo te lo dice la experiencia personal.

destroyer Ver Perfil del Miembro Ver los mensajes de este miembro	Mar 17 2013, 12:00 PM Publicado: #10
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 576 Registrado: 24-November 11 Miembro Nº: 97.702 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	El ángulo lo que te da es una inferencia de la pendiente cerca del punto, es decir que al trabajar con bolas en el espacio (equivalente a decir polares en R2), indica una independencia en la trayectoria cercana al límite. Eso basta para concluir el enunciado, independiente de la "velocidad" que tome. En estos ejercicios siempre hay que ocupar como último recurso éste hecho, lo primero y más facil es comprobar que el enunciado no es correcto, iterando o haciendo cualquier maniobra.

« Posterior · Cálculo en Varias Variables · Anterior »

2 Páginas:

1 2 >

Reply to this topic

Start new topic

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 4th April 2025 - 02:54 PM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.