|
|
|
|
|
|
|
  |
 Jun 6 2009, 09:37 PM Jun 6 2009, 09:37 PM
Publicado:
#1
|
|
 Dios Matemático Supremo Grupo: Colaborador Platinum Mensajes: 824 Registrado: 15-October 07 Desde: Valparaíso Miembro Nº: 11.342 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Sea
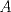 una matriz de orden una matriz de orden 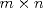 . Demuestre que el sistema no homogeneo . Demuestre que el sistema no homogeneo 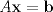 tiene solución si y sólo si tiene solución si y sólo si 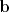 es ortogonal a toda solución del sistema homogeneo es ortogonal a toda solución del sistema homogeneo 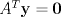 . .Saludos -------------------- Pedro P. Montero Silva Estudiante de Licenciatura en Ciencias, Mención Matemática - Mechón 2009 "One rather curious conclusion emerges, that pure mathematics is on the whole distinctly more useful than applied. A pure mathematician seems to have the advantage on the practical as well as on the aesthetic side. For what is useful above all is technique, and mathematical technique is taught mainly through pure mathematics." G.H. Hardy |
|
|
|
 May 5 2015, 11:32 PM May 5 2015, 11:32 PM
Publicado:
#2
|
|
 Dios Matemático Supremo Grupo: Super Moderador Mensajes: 1.912 Registrado: 10-January 08 Desde: Un Sobolev Miembro Nº: 14.530 Nacionalidad:  Sexo:  |
Sea 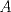 una matriz de orden una matriz de orden 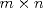 . Demuestre que el sistema no homogeneo . Demuestre que el sistema no homogeneo 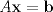 tiene solución si y sólo si tiene solución si y sólo si 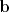 es ortogonal a toda solución del sistema homogeneo es ortogonal a toda solución del sistema homogeneo 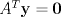 . .Saludos La famosa Alternativa de Fredholm. ![TEX: <br />\noindent ($\Rightarrow$) Supongamos por el contrario que $b\in \mathrm{Im\,}A$ (o sea, que $Ax=b$, tiene solución) y que $\langle b,v\rangle=v^Tb\neq 0$ para algún $v$ tal que $A^Tv=\theta$ (en palabras simples, que $b\notin [\ker(A^T)]^{\perp}$). Pero <br />$$(A^Tv)^T=\theta\Rightarrow v^TA=\theta\Rightarrow v^TAx=0\Rightarrow v^Tb=0$$<br />una contradicción. <br /><br />](/tex-image/aef2286fe9789e633ed38d07800eea32.png) ![TEX: <br />\noindent ($\Leftarrow$) Supongamos por el contrario que $b\in [\ker(A^T)]^{\perp}$ pero $b\notin \mathrm{Im\,}A$. Luego $Ax\neq b$, para todo $x\in \mathbb{R}^n$. Pero si $v$ es tal que $A^Tv=\theta$, debe tenerse que $\langle b,v\rangle=v^Tb= 0$, y:<br />$$Ax\neq b\Rightarrow x^TA^T\neq b^T\Rightarrow x^TA^Tv\neq b^Tv\Rightarrow x^T\theta \neq b^Tv\Rightarrow\theta x\neq v^Tb\Rightarrow v^Tb\neq 0$$<br />una contradicción. <br /><br />](/tex-image/021841b2a6c4c31702f6bb02dec1811f.png)
-------------------- |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 23rd November 2024 - 04:41 PM |









