|
|
|
|
|
|
|
  |
 Nov 7 2009, 03:24 AM Nov 7 2009, 03:24 AM
Publicado:
#81
|
|
|
Dios Matemático Supremo Grupo: Super Moderador Mensajes: 2.065 Registrado: 25-May 08 Desde: Pelotillehue Miembro Nº: 24.463 |
Aunque el TNP es profundo se tienen pruebas simples y elementales de él. Aún así, estaría bien dar con el enfoque sencillo que mencionas. Por favor, no lo postees todavía. Seguramente hay varios compañeros que se encuentran en su búsqueda. Dejo en todo caso mi VoF y el primero que encuentre la otra solución al VoF previo de Pasten puede publicarla en este thread para hacerse merecedor a su dotación respectiva de bragging rights.
VoF: Supongamos que 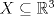 es homeomorfo a es homeomorfo a 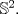 Del teorema de Jordan-Brouwer se sigue que Del teorema de Jordan-Brouwer se sigue que 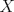 divide a divide a 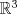 en una componente acotada y en una no-acotada. Sea en una componente acotada y en una no-acotada. Sea 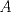 dicha componente no acotada. ¿Es el interior de dicha componente no acotada. ¿Es el interior de 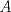 necesariamente homeomorfo al interior del complemento en necesariamente homeomorfo al interior del complemento en 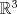 de de 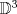 ? ?
-------------------- "Please forget everything you have learned in school; for you haven't learned it... Please keep in mind at all times the corresponding portions of your school curriculum; for you haven't actually forgotten them." -- E. Landau
|
|
|
|
 Nov 9 2009, 10:57 AM Nov 9 2009, 10:57 AM
Publicado:
#82
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 765 Registrado: 6-December 05 Miembro Nº: 458 Nacionalidad:  Sexo:  |
Aunque el TNP es profundo se tienen pruebas simples y elementales de él. Aún así, estaría bien dar con el enfoque sencillo que mencionas. Por favor, no lo postees todavía. Seguramente hay varios compañeros que se encuentran en su búsqueda. Dejo en todo caso mi VoF y el primero que encuentre la otra solución al VoF previo de Pasten puede publicarla en este thread para hacerse merecedor a su dotación respectiva de bragging rights. VoF: Supongamos que 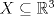 es homeomorfo a es homeomorfo a 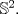 Del teorema de Jordan-Brouwer se sigue que Del teorema de Jordan-Brouwer se sigue que 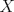 divide a divide a 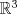 en una componente acotada y en una no-acotada. Sea en una componente acotada y en una no-acotada. Sea 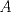 dicha componente acotada. ¿Es el interior de dicha componente acotada. ¿Es el interior de 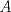 necesariamente homeomorfo al interior del complemento en necesariamente homeomorfo al interior del complemento en 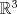 de de 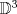 ? ?Claramente hay un problema con el enunciado... Saludos -------------------- Pasten, un buen muchacho en quien confiar.
|
|
|
|
 Nov 9 2009, 02:43 PM Nov 9 2009, 02:43 PM
Publicado:
#83
|
|
|
Dios Matemático Supremo Grupo: Super Moderador Mensajes: 2.065 Registrado: 25-May 08 Desde: Pelotillehue Miembro Nº: 24.463 |
Editado.
-------------------- "Please forget everything you have learned in school; for you haven't learned it... Please keep in mind at all times the corresponding portions of your school curriculum; for you haven't actually forgotten them." -- E. Landau
|
|
|
|
 Dec 10 2009, 10:22 AM Dec 10 2009, 10:22 AM
Publicado:
#84
|
|
|
Dios Matemático Supremo Grupo: Super Moderador Mensajes: 2.065 Registrado: 25-May 08 Desde: Pelotillehue Miembro Nº: 24.463 |
... la idea es la misma pero con un resultado mas facil de probar. Hola Pasten, Con resultado más fácil de probar te referías a las desigualdades de Chebyshev con las que se establece que 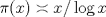 ? ?
-------------------- "Please forget everything you have learned in school; for you haven't learned it... Please keep in mind at all times the corresponding portions of your school curriculum; for you haven't actually forgotten them." -- E. Landau
|
|
|
|
 Dec 10 2009, 02:22 PM Dec 10 2009, 02:22 PM
Publicado:
#85
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 765 Registrado: 6-December 05 Miembro Nº: 458 Nacionalidad:  Sexo:  |
Hola Pasten, Con resultado más fácil de probar te referías a las desigualdades de Chebyshev de las que se concluye que 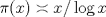 ? ?Mas facil, aunque eso funciona. La serie de los reciprocos de los primos diverge porque la armonica diverge. Por otro lado, una suma finita de series p con p>1 converge, asi que salvo pequeños ajustes (no dividir por terminos nulos) esto prueba lo que queremos. Saludos -------------------- Pasten, un buen muchacho en quien confiar.
|
|
|
|
 Jan 20 2010, 05:58 PM Jan 20 2010, 05:58 PM
Publicado:
#86
|
|
|
Dios Matemático Supremo Grupo: Super Moderador Mensajes: 2.065 Registrado: 25-May 08 Desde: Pelotillehue Miembro Nº: 24.463 |
VoF: Supongamos que 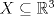 es homeomorfo a es homeomorfo a 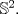 Del teorema de Jordan-Brouwer se sigue que Del teorema de Jordan-Brouwer se sigue que 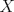 divide a divide a 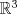 en una componente acotada y en una no-acotada. Sea en una componente acotada y en una no-acotada. Sea 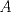 dicha componente no acotada. ¿Es el interior de dicha componente no acotada. ¿Es el interior de 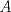 necesariamente homeomorfo al interior del complemento en necesariamente homeomorfo al interior del complemento en 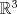 de de 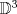 ? ?¿Quién pone la respuesta pues? -------------------- "Please forget everything you have learned in school; for you haven't learned it... Please keep in mind at all times the corresponding portions of your school curriculum; for you haven't actually forgotten them." -- E. Landau
|
|
|
|
 Jan 27 2010, 10:35 AM Jan 27 2010, 10:35 AM
Publicado:
#87
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 765 Registrado: 6-December 05 Miembro Nº: 458 Nacionalidad:  Sexo:  |
¿Quién pone la respuesta pues? Ver la esfera de alexander ("alexander horned sphere" si quieren buscar en wikipedia). El problema es que esto es super conocido, se ve en cualquier curso de topologia algebraica. Saludos Mensaje modificado por Pasten el Jan 27 2010, 10:35 AM -------------------- Pasten, un buen muchacho en quien confiar.
|
|
|
|
 Jan 27 2010, 10:58 AM Jan 27 2010, 10:58 AM
Publicado:
#88
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 560 Registrado: 24-December 09 Miembro Nº: 64.629 |
Ver la esfera de alexander ("alexander horned sphere" si quieren buscar en wikipedia). El problema es que esto es super conocido, se ve en cualquier curso de topologia algebraica. Saludos Pero no todos tienen un curso de " Topología Algebraica". Hasta un alumno egresado de licenciatura en matemática y posteriormente magister puede no verlo pues generalmente ese curso se da en calidad de electivo, por ende no es " super conocido" , eso es ironía ( igual me rei). |
|
|
|
 Jan 27 2010, 01:00 PM Jan 27 2010, 01:00 PM
Publicado:
#89
|
|
|
Dios Matemático Supremo Grupo: Super Moderador Mensajes: 2.065 Registrado: 25-May 08 Desde: Pelotillehue Miembro Nº: 24.463 |
La única ironía aquí es que el máximo detractor de la Wikipedia se remita a ella para salir avante en la ocasión presente.
-------------------- "Please forget everything you have learned in school; for you haven't learned it... Please keep in mind at all times the corresponding portions of your school curriculum; for you haven't actually forgotten them." -- E. Landau
|
|
|
|
 Jan 27 2010, 04:26 PM Jan 27 2010, 04:26 PM
Publicado:
#90
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 765 Registrado: 6-December 05 Miembro Nº: 458 Nacionalidad:  Sexo:  |
La única ironía aquí es que el máximo detractor de la Wikipedia se remita a ella para salir avante en la ocasión presente. no no, soy detractor de la gente cuyos conocimientos solo son copy-paste de internet, pero usualmente los temas no tan "pop" de wikipedia los coloca gente que si sabe, como referencia rapida es excelente pero para estudiar no sirve, no reemplaza un curso. Personalmente, eso lo estudie en el Hatcher de topologia algebraica cuando hice el curso pero no voy a subir un libro para responder en el foro... Saludos -------------------- Pasten, un buen muchacho en quien confiar.
|
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 3rd April 2025 - 02:42 AM |










