Como elevar al cuadrado, ...un numero terminado en 5 Opciones

[shadoweps]

Hola Kenshin, Solo quiero agradeser la ayuda, gracias por tu paciencia y poder explicarme detalladamente el proceso

Tambien gracias a Xsebastian por su explicacion

Salu2

[Camila_Espinoza]

a se pasaron esta super buenap , pero nos servira eso en la psu??

[Rurouni Kenshin]

a se pasaron esta super buenap , pero nos servira eso en la psu??

Por supuesto que si...o sea en mas de una ocasion he tenido la oportunidad de aplicar un razonamiento de calculo mental como este en problemas psu...es clasico escuchar que dicen que no les alcanza el tiempo para hacer la psu..pero en realidad si uno se da cuenta, la mayor demora que uno tiene esta en los calculos..mas que en los razonamientos...
La prueba deberia por lo menos poder revisarse una vez completa...esa diferencia de rapidez de resolucion la marca la velocidad de calculo..al menos desde mi punto de vista...
Saludos

[ffsll]

al multiplicar por 11, se mantiene el extremo derecho (del numero que se multiplicara por 11), y se suman de dos en dos, de derecha a izquierda, y dicha suma se coloca en el mismo orden, cuando la suma supere el número 10, se le suma “uno” al siguiente numero , de esta forma hasta llegar al ultimo numero, que se escribe igual, amenos que la suma anterior sea mayor que 10, porque ahí se le sumara “uno”.

ejemplo

14525 x 11 = 159775

5 = extremo derecho
7 = 5+2
7 = 2+5
9 = 5+4
5 = 4+1
1 = primer numero, como el anterior es menor a 10, se mantiene

saludos, un año despues jajajaja des ultimo post.

Mensaje modificado por ffsll el Nov 30 2006, 12:32 PM

[Ocioman]

waaa!
la cagó
se agradece mucho
son muy secos
=D
algun día subiré
mis tecnicas
(esas no las conocía)

[TM2K4]

Estuve pensando un poco en como ocupar la fórmula a^2= (a-b)(a+b) + b^2, y se me ocurrió esto:

Para elevar un número al cuadrado, podemos encontrar el múltiplo de 5 que lo antecede, y éste será b en nuestra fórmula, pues ya sabemos elevar al cuadrado números terminados en 5 y en 0. Así, 17^2 lo podemos expresar como:

17^2 = (17 + 15)(17 - 15) + 15^2
= 32*2 + 225 = 64 + 225 = 289

La gracia de esto, es que en la parte (a-b) nos quede un número relativamente pequeño, para que podamos multiplicar mentalmente...

Ahora, otra forma es lograr formar en algunos de los terminos (a+b) o (a+b) un multiplo de 10, sumando lo q falte para la decena mas cercana, creo q es mucho mas facil.
(la idea es q en la parte de 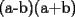termines multiplicando por algo terminado en 0), y el 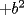quede un numero pequeño

por ejemplo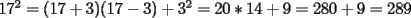



la idea es ver que decena queda mas cerca, en este caso salia mas facil llegar de 17 a 20,(ocupando (a+b) si hubiese sido 14 es mejor irse por la decena inferior, o sea pensar en acomodarse en el lado (a-b)

ej: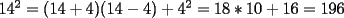

al final cosa de gustos, con los multiplos de 5 ocupas la tecnica aprendida anteriormente, con esta otra sale mas practico multiplicar por algún multiplo de 10.

Saludos!

[DavidC]

Esta muy bueno.
Yo en tiempo de ocio saque uno que es un poco mas rapido y lento a la vez (es que es mas corto pero es casi lo mismo que calcular el mismo numero :S aaaa que estoy diciendo).
Bueno es asi y muy facil de demostrar:
x² = (x - 1)² + 2(x - 1) + 1
Prueben con distintos numeros.
La demostracion:
x² = x² - 2x + 1 + 2x - 2 + 1
Simplificando todo:
x² = x²

[Manuel Fco]

Aunque es viejo el tema, nunca lo había visto, está genial

[g.l.torres]

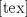hola, soy nuevo en esto pero aqui escribo un poco

en mis ratos de ocio pude ver unas formulitas para pasar de un numero al cuadrado al otro consecutivo tambien al cuadrado, osea de (a,a+1)

b^2=a^2 +(a+b) , con b=a+1 ( para todos los numeros consecutivos )

b^3=a^3 + (3ab +1), con b=a+1 este es = pero para los numeros al cubo

ej: 2^2=1^2 + (1+2)=4 sirve para todos los numeros consecutivos

2^3=1^3 + (3*2*1 + 1)=8 lo mismo q arrriba

no se si servira de mucho pero = lo quise poner, tambien me separa lso numeros a la cuarta pero ahora no me acuerdo
ya po eso era mi aporte, si ai algo malo m avisan no ma'>

Mensaje modificado por g.l.torres el Aug 25 2009, 11:05 PM

[OckUC]

Revisé que había una técnica similar a ésta en este topic (esa de descomponer en centenas, decenas, unidades, etc y calcular el cuadrado de ese polinomio):

Por ejemplo, para números de dos cifras:

Si queremos saber el cuadrado de 29, podemos reescribirlo como: (30-1)
Se eleva al cuadrado y se aplica la fórmula de cuadrado de binomio:

29^2=(30-1)^2=30^2-2*30+1=900-60+1=841

La técnica es muy útil porque cualquier número se puede expresar como una suma o diferencia de múltiplos de potencias de 10. (Y claro, a la hora de multiplicar hay que saberse solamente los cuadrados de números de 1 dígito y el resto es agregar solo ceros y multiplicar números pequeños). Y al final se suma todo lo obtenido.

Otro ejemplo:

El cuadrado de 361?

361^2=(400-39)^2=400^2-2*400*39+39^2

Se puede reaplicar la técnica para calcular 39^2

Reescribiremos 39=(40-1)

(40-1)^2=40^2-2*40+1
Continuando...

361^2=400^2-2*400*(40-1)+(40-1)^2=400^2 -2*400*40 +2*400 +40^2 -2*40 +1=

361^2= 160000-32000+800+1600-80+1= 130321

Pueda que el desarrollo se vea un poco largo, pero la idea es siempre simplificar el cálculo para el ahorro de tiempo.

Mensaje modificado por OckUC el Aug 26 2009, 01:06 AM