|
|
|
|
|
|
|
  |
 Aug 13 2005, 02:32 AM Aug 13 2005, 02:32 AM
Publicado:
#1
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
Bueno...esta es una tecnica muy simpatica para elevar al cuadrado numeros terminados en 5.
O sea esta tecnica nos deberia servir para calcular expresiones como 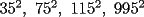 , etc... , etc...Ejemplo: Para calcular 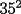 , miremos al 35.Luego tapenle el 5 con el dedo , miremos al 35.Luego tapenle el 5 con el dedo Eso nos dejaria a la vista un 3. Luego ese 3 multiplicalo por su sucesor(o sea 4) lo cual nos daria 3x4=12 Finalmente al resultado obtenido(o sea 12) pegale un 25 al final( 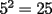 )...y vuala!!!!!...nos queda )...y vuala!!!!!...nos queda 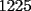 que es el resultado buscado. que es el resultado buscado.Pegarle..quiere decir colocar a continuacion...o sea despues del 12 escribir un 25,formando asi un numero de 4 cifras. Esto no deja de ser muy interesante...pero para que quede mas claro veamos un ejemplo mas. Para calcular 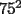 ,tapemos el 5 y nos queda un 7.Luego multipliquemos 7 por su sucesor(o sea 8) obteniendo 56.Finalmente a este numero peguenle un 25 al final. ,tapemos el 5 y nos queda un 7.Luego multipliquemos 7 por su sucesor(o sea 8) obteniendo 56.Finalmente a este numero peguenle un 25 al final. El resultado es entonces 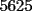 Pero ahora la duda vendria...como seria con 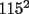 ? ?Para calcular 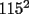 , tapemos el 5 y nos queda 11.Ahora 11x12=132 , tapemos el 5 y nos queda 11.Ahora 11x12=132Finalmente el resultado es 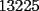 (Lo que mas les cuesta es 11x12,jejejejeje) Sera posible calcular 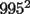 ? ? Tapando el 5 nos queda un 99, y 99x100=9900(se agregan dos ceros) Finalmente el resultado es 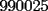 Ahora esta tecnica logicamente tiene sus limitantes...por ejemplo si quieren calcular 365^2 tienen que saber calcular 36x37 lo cual no es directo...pero para numeritos chicos sirve muy bien Es increible cuando uno pregunta en un salon de clases 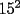 y responden 115 o bien dicen que no saben. y responden 115 o bien dicen que no saben.Para sacar 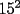 tapamos el 5,queda un 1, y 1x2....emmm...2 tapamos el 5,queda un 1, y 1x2....emmm...2 Luego la respuesta es 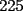 Con 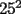 calculen 2x3=6 y la respuesta sera calculen 2x3=6 y la respuesta sera 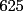 Bueno...la idea seria primero tratar de descubrir el porque funciona algo tan simpatico....o sea crear una demostracion de esta tecnica. Luego de crear la demostracion ver como la tecnica se puede generalizar para numeros con cualquier terminacion y no necesariamente 5 Algunos creen que es lo mismo si termina en 6,colocando 36 al final en vez de 25(pues 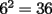 ) )Pero eso es falso porque basta calcular 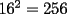 para convencerse de que no siempre todo funciona bonito para convencerse de que no siempre todo funciona bonito Espero les haya gustado..espero sus comentarios...en especial de los que recien estan empezando en el foro para que se den cuenta que la idea de los administradores y moderadores es partir de cero..hacer un entrenamiento desde lo mas basico via web...con el unico afan de darles a ustedes las oportunidades que quizas nosotros no tuvimos en nuestra juventud. Aprovechen a fmat..que es de ustedes..el foro no lo hacen los moderadores ni los administradores...sino ustedes...los usuarios que estan siempre leyendo cosas en fmat..la idea es que ahora se atrevan a postear....asi que los espero...si quieren mas simpatias como esta o muchas otras..no tienen mas que pedirlo..y lo tendran... Saludos -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
 Aug 13 2005, 08:38 PM Aug 13 2005, 08:38 PM
Publicado:
#2
|
|
 Matemático Grupo: Usuario FMAT Mensajes: 68 Registrado: 9-August 05 Desde: Rancagua Miembro Nº: 206 Nacionalidad:  Sexo:  |
Tengo una demostración ^^
Cualquier número terminado en 5 se puede escribir como 10a + 5 ej: 5 = 10x0 + 5 15 = 10x1 + 5 215 = 10x21 + 5, etc. Entonces, (10a+5)^2 = 100a^2 + 100a + 25 = 100a(a+1) + 25 Si nos fijamos, ese a(a+1) quiere decir que estamos multiplicando la(s) cifra(s) distintas de la unidad, que es 5, por su sucesor. Luego que hagamos la multiplicación de a por su sucesor, debemos "pegarle 25" ...¿Qué quiere decir esto?... Multiplicar por 100 y sumar 25, que es lo que le estamos haciendo a a(a+1). Espero que se haya entendido ^^ Mata ne! |
|
|
|
 Aug 13 2005, 11:03 PM Aug 13 2005, 11:03 PM
Publicado:
#3
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
CITA(Fushigi-kun @ Aug 13 2005, 09:38 PM) Tengo una demostración ^^ Cualquier número terminado en 5 se puede escribir como 10a + 5 ej: 5 = 10x0 + 5 15 = 10x1 + 5 215 = 10x21 + 5, etc. Entonces, (10a+5)^2 = 100a^2 + 100a + 25 = 100a(a+1) + 25 Si nos fijamos, ese a(a+1) quiere decir que estamos multiplicando la(s) cifra(s) distintas de la unidad, que es 5, por su sucesor. Luego que hagamos la multiplicación de a por su sucesor, debemos "pegarle 25" ...¿Qué quiere decir esto?... Multiplicar por 100 y sumar 25, que es lo que le estamos haciendo a a(a+1). Espero que se haya entendido ^^ Mata ne! Excelentisima demostracion..felicitaciones..que gusto tener buenos integrantes en fmat...que no solo saben harto..sino que tambien saben explicar las cosas de manera muy clara Sigue asi... Y ahora la idea seria generalizar la tecnica... Para ello mi pista es basarse en la suma por su diferencia... Noten que es cierto que a^2 =(a+b)(a-b) + b^2 Veamos como nos va con eso Saludos -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
 Aug 15 2005, 08:29 PM Aug 15 2005, 08:29 PM
Publicado:
#4
|
|
|
Principiante Matemático Grupo: Usuario FMAT Mensajes: 11 Registrado: 14-August 05 Desde: Concepción Miembro Nº: 234 |
Tengo la generalización de la tecnica, y la ocupo muy seguido para calcular el cuadrado de cualquier número Entero.
Como dijo Fushigi-kun, lo números se pueden expresar de las siguientes formas: de una cifra -> 3 = 3 de dos cifras -> 16 = 1*10 + 6 queda de la forma 10a + b de tres cifras -> 234 = 2*100 + 3*10 + 4 queda de la forma 100a + 10b + c y así sucesivamente... Cuadrado de un número de una cifra... weno es fácil memorizar todos los casos... 1^2 = 1 2^2 = 4 3^2 = 9 4^2 = 16 5^2 = 25 6^2 = 36 7^2 = 49 8^2 = 64 9^2 = 81 Cuadrado de un número de dos cifras: acá se complica un poko, pero es más corto que multiplicar el número por si mismo. (10a + b)^2 = 100a^2 + 20ab + b^2 Entonces lo que hago es sacar el cuadrado de cada cifra, luego multiplico las dos cifras y reemplazo. Supongamos que el número es 37, tenemos que encontrar el cuadrado de 37. (10*3 + 7)^2 = 100*9 + 20*21 + 49. Se ve hermoso cuando se expresa en una suma vertical: 900 420 + 49 1.369 Desde luego, todas estas operaciones se pueden hacer mentalmente, sin papel ni lápiz. Cuadrado de un número de tres cifras: Se puede expresar de la forma : 100a + 10b + c y su cuadrado sería: (100a + 10b + c)^2 = 10000a^2 + 100b^2 + c^2 + 2000ab + 200ac + 20bc Sacamos los cuadrados de cada cifra (a, b, c) luego multiplicamos de a dos cifras (ab, ac, bc) y reemplazamos los resultados en la formulita , luego se suma todo. Ejemplo: el cuadrado de 234 (2*100 + 3*10 + 4)^2 = 10000*4 + 100*9 + 16 + 2000*6 + 200*8 + 20*12 = 40.000 900 16 12.000 1.600 + 240 54.756 Sé que a la mayoría no le gustó mi tecnica, pero a mí me da flojera multiplicar número por número y me gusta complicarme la vida tratando de buscar métodos más fáciles para ahorrar tiempo. esop, Análogicamente se puede usar este método para calcular el cuadrado de números con más de 3 cifras También se puede sacar el Cubo y otras potencias del mismo número utilizando estos métodos algebraicos de expresar el número en la suma de productos de las cifras del número con su respectiva potencia de 10. Espero que en algo haya ayudado, porque no me gusta dar jugo. A todo esto... La página está muy buena. Felicitaciones a todo el equipo Administrador del FMAT!!! No he podido despegarme desde que me registré. Creo que eso es bueno. AdioZZZZZ. -------------------- "La imaginación es más importante que el conocimiento" Albert Einstein.
|
|
|
|
 Aug 16 2005, 08:12 PM Aug 16 2005, 08:12 PM
Publicado:
#5
|
|
|
Principiante Matemático Grupo: Usuario FMAT Mensajes: 4 Registrado: 5-August 05 Miembro Nº: 161 |
aunke no postee en esta página la ocupo en reiteradas ocasiones... y conste q la recomiendo. La técnik del cuadrado es muy eficiente y vaya q sirve!!! ahorra mucho tiempo...papel y lapiz. Ya hay varias compañeras de mi curso que la saben jeje Me alegra saber q hayan foros como este, de cosas que nos sirven, de donde podemos sacar algo, o mejor dicho, de donde podamos aprender. =) Se les felicita a los administradores |
|
|
|
 Sep 5 2005, 10:08 PM Sep 5 2005, 10:08 PM
Publicado:
#6
|
|
 Matemático Grupo: Usuario FMAT Mensajes: 68 Registrado: 9-August 05 Desde: Rancagua Miembro Nº: 206 Nacionalidad:  Sexo:  |
Estuve pensando un poco en como ocupar la fórmula a^2= (a-b)(a+b) + b^2, y se me ocurrió esto:
Para elevar un número al cuadrado, podemos encontrar el múltiplo de 5 que lo antecede, y éste será b en nuestra fórmula, pues ya sabemos elevar al cuadrado números terminados en 5 y en 0. Así, 17^2 lo podemos expresar como: 17^2 = (17 + 15)(17 - 15) + 15^2 = 32*2 + 225 = 64 + 225 = 289 La gracia de esto, es que en la parte (a-b) nos quede un número relativamente pequeño, para que podamos multiplicar mentalmente... |
|
|
|
 Sep 24 2005, 12:31 PM Sep 24 2005, 12:31 PM
Publicado:
#7
|
|
 Principiante Matemático Destacado Grupo: Usuario FMAT Mensajes: 28 Registrado: 22-September 05 Desde: Merida, Mexico Miembro Nº: 322 Nacionalidad:  Sexo:  |
Holap, la vdd que muy buenas sus aportaciones io no sabia eso, y la vdd es muy facil, pero tengo una duda espero me ayuden
CITA Tengo una demostración ^^ Cualquier número terminado en 5 se puede escribir como 10a + 5 ej: 5 = 10x0 + 5 15 = 10x1 + 5 215 = 10x21 + 5, etc. Entonces, (10a+5)^2 = 100a^2 + 100a + 25 = 100a(a+1) + 25 Si nos fijamos, ese a(a+1) quiere decir que estamos multiplicando la(s) cifra(s) distintas de la unidad, que es 5, por su sucesor. Luego que hagamos la multiplicación de a por su sucesor, debemos "pegarle 25" ...¿Qué quiere decir esto?... Multiplicar por 100 y sumar 25, que es lo que le estamos haciendo a a(a+1). Espero que se haya entendido ^^ Mata ne! No entendi como salio ese a(a+1) Salu2 -------------------- Todos se rien de mi por que soy diferente, Yo me rio de ustedes por que son Todos iguales.
 |
|
|
|
 Sep 24 2005, 03:56 PM Sep 24 2005, 03:56 PM
Publicado:
#8
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
El paso que no comprendiste, fue el siguiente:
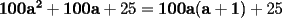 Intentando ser más detallista, haría lo siguiente: 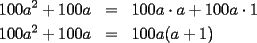 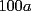 es un factor común. Visto de atrás hacia adelante, tenemos lo siguiente, porque hay una propiedad conocida como propiedad distributiva: es un factor común. Visto de atrás hacia adelante, tenemos lo siguiente, porque hay una propiedad conocida como propiedad distributiva: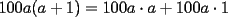 -------------------- |
|
|
|
 Sep 24 2005, 06:24 PM Sep 24 2005, 06:24 PM
Publicado:
#9
|
|
 Principiante Matemático Destacado Grupo: Usuario FMAT Mensajes: 28 Registrado: 22-September 05 Desde: Merida, Mexico Miembro Nº: 322 Nacionalidad:  Sexo:  |
CITA El paso que no comprendiste, fue el siguiente: 100a²+100a+25=100a(a+1)+25 Ese paso no es truculento, por eso aparece sin explicación. Lo que hizo fue sacar factor común, o como se dice entre gente educada: "factorizar" Intentando ser más detallista, haría lo siguiente: 100a²+100a=100a·a+100a·1 100a²+100a=100a(a+1) Aer si ya entendi 100a²+100a+25=100a(a+1)+25 el a(a+1) se pone como forma para no repetir 100a²+100a? por eso queda 100a²+100a+25=100a(a+1)+25 Pero tambien se puede poner 100a²+100a+25=100a²+100a+25 sin factorizarlo? Muchas gracias por responder a mi duda anterior, esque soy muy nuevo en esto de las matematicas, apenas ahora me empeze a interesar mucho en ellas y ahorita en la preparatoria estoy en matematicas Salu2 -------------------- Todos se rien de mi por que soy diferente, Yo me rio de ustedes por que son Todos iguales.
 |
|
|
|
 Sep 24 2005, 11:45 PM Sep 24 2005, 11:45 PM
Publicado:
#10
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
CITA(shadoweps @ Sep 24 2005, 07:24 PM) Aer si ya entendi 100a²+100a+25=100a(a+1)+25 el a(a+1) se pone como forma para no repetir 100a²+100a? por eso queda 100a²+100a+25=100a(a+1)+25 Pero tambien se puede poner 100a²+100a+25=100a²+100a+25 sin factorizarlo? Muchas gracias por responder a mi duda anterior, esque soy muy nuevo en esto de las matematicas, apenas ahora me empeze a interesar mucho en ellas y ahorita en la preparatoria estoy en matematicas Salu2 Por supuesto que se puede poner de ambas formas,siendo ambas validas...pero el ponerlo de la forma 100a(a+1)+25 nos dice que multipliquemos a y su sucesor(a(a+1)) y eso lo multipliquemos por 100,lo cual equivale a agregarle 2 ceros al valor de a(a+1) por la derecha.Luego le sumas 25 al resultado final,pero como 100a(a+1) termina en 2 ceros,entonces sumarle 25 equivale a pegarle al final un 25 al valor de a(a+1)(sin multiplicarlo por 100) Eso justifica el metodo que hemos explicado....para calcular 25^2,35^2 o bien 115^2.En el primer caso a=2,en el segundo a=3 y en el tercero a=11 Espero haber aclarado tu duda...cualquier duda de lo explicado o algo extra..solo tienes que hacerla -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 18th February 2025 - 05:01 PM |










