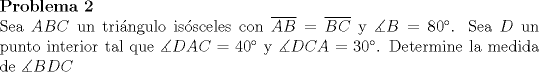Cuarto Nivel - Segunda Fecha CMAT Media

Foro fmat.cl > Sector Preparación Olimpiadas > Competencias y Olimpiadas > Campeonato Interescolar > Campeonato Interescolar 2009 > Segunda Fecha

2 Páginas:

< 1 2

Cuarto Nivel - Segunda Fecha CMAT Media

Opciones

carolina fca Ver Perfil del Miembro Ver los mensajes de este miembro	Jun 2 2009, 06:56 PM Publicado: #11
Principiante Matemático Grupo: Usuario FMAT Mensajes: 13 Registrado: 16-July 08 Miembro Nº: 30.099 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	era 100º el dos pero no se hacer lso dibujos aki!! >.< --------------------

sí-sí el residen... sí-sí el residente Ver Perfil del Miembro Ver los mensajes de este miembro	Jun 2 2009, 09:24 PM Publicado: #12
Puntaje Nacional PSU Matemáticas Admisión 2010 Grupo: Colaborador Gold Mensajes: 390 Registrado: 22-July 07 Desde: la granja Miembro Nº: 7.754 Nacionalidad: Colegio/Liceo: Sexo:	Notar que como es isósceles y el ángulo apuesto a la base vale 80°, lo ángulos basales valen 50°. Ahora trazamos la altura hacia la base, y sea E donde esta corta a DC, y se F donde cae la altura sobre el lado AC. 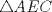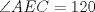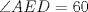Dibujo.PNG ( 8.55k ) Número de descargas: 6 Trazamos AE, y notar que se forma el triangulo isósceles $TEX: $\triangle AEC$$ de ángulos basales de medida 30°, por tanto $TEX: $\angle AEC=120$$ , entonces $TEX: $\angle AED= 60$$ ya que forman un par lineal. 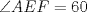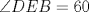Como se trazó la altura a un isósceles, esta es bisectriz del ángulo de 120°, entonces $TEX: $\angle AEF= 60$$ por tanto $TEX: $\angle DEB= 60$$ . 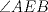De esto se tiene que DE es bisectriz de $TEX: $\angle AEB$$ . 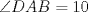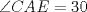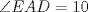Ahora como dijimos que los ángulos basales del triángulo mayor valian 50, se tiene que $TEX: $\angle DAB=10$$ , y como $TEX: $\angle CAE=30$$ , entonces $TEX: $\angle EAD=10$$ . 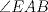Entonces DA es bisectriz de $TEX: $\angle EAB$$ . Por tanto D es incentro del triangulo AEB. Ahora como D es incentro, se tiene que DB es bisectriz y de esto se tiene que 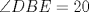$TEX: $\angle DBE= 20$$ Luego por suma interior de ángulos se tiene que 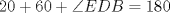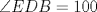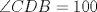$TEX: $20+60+\angle EDB=180$$ $TEX: $\angle EDB=100$$ $TEX: $\angle CDB=100$$ -------------------- ...

GohanSSJ2 Ver Perfil del Miembro Ver los mensajes de este miembro	Jun 3 2009, 12:03 PM Publicado: #13
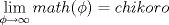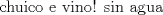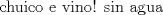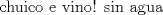Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 140 Registrado: 15-May 08 Desde: Rancagua/ Valpo Miembro Nº: 23.226 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	gracias no se me habia ocurrido analizarla de esa forma jojo todavia me falta mucho -------------------- $TEX: $\displaystyle \lim_{\phi\rightarrow \infty}math(\phi) =chikoro$$ $TEX: chuico e vino! sin agua$ $TEX: chuico e vino! sin agua$ $TEX: chuico e vino! sin agua$ $TEX: Liceo de Rancagua$

Kaissa Ver Perfil del Miembro Ver los mensajes de este miembro	Feb 7 2010, 03:48 PM Publicado: #14
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad: Colegio/Liceo: Sexo:	CITA(Rurouni Kenshin @ May 30 2009, 11:26 PM) $TEX: <br />\noindent\textbf{Problema 2}\\<br />Sea $ABC$ un triángulo isósceles con $\overline{AB}=\overline{BC}$ y $\measuredangle B=80^{\circ}$. Sea $D$ un punto interior tal que $\measuredangle DAC=40^{\circ}$ y $\measuredangle DCA=30^{\circ}$. Determine la medida de $\measuredangle BDC$$ $TEX: $ $\\<br />Posteo mi soluci\'on alternativa a este antiguo problema......xd\\<br />$ $\\<br />Extendamos $\overline{DC}$ m\'as all\'a de $D$ hasta un punto $X$ tal que $\overline{BC}=\overline{BX}$ (como m\'as de alguno preguntar\'a \textit{y por qu\'e debe existir efectivamente este punto $X$?} propongo esta construcci\'on alternativa para dicho punto: Tr\'acese la altura $h_{B}$ de $\Delta CDB$ desde $B$ y sea $X$ es reflejo de $C$ respecto de $h_{B}$.)\\<br />Por diferencia dde \'angulos sacamos $\angle ABX=60^{\circ}$ y as\'i $\Delta ABX$ es equil\'atero.\\<br />Por otro lado $\angle DXA=60-20=40^{\circ}$ y $\angle DAX=60+\angle DAB=70^{\circ}$; lo cu\'al muestra que $\Delta DXA$ es is\'osceles en $X$.\\<br />Finalmente $\angle DBA=\angle DBX-\angle ABX=80-60=20^{\circ}$.\\<br />Entonces $\angle CBD=60^{\circ}$ y por suma de \'angulos en $\Delta CDB$ sacamos que $\angle CDB=180-(20+60)=100^{\circ}$<br />$ -------------------- Este es un extracto de Qué es fmat by Kenshin. La pregunta para ti estimado(a) lector(a) es... ¿Qué haces tu para que ésto se cumpla?

Newtype Ver Perfil del Miembro Ver los mensajes de este miembro	Feb 7 2010, 06:49 PM Publicado: #15
Dios Matemático Supremo Grupo: Team Ensayos FMAT Mensajes: 1.559 Registrado: 18-November 07 Miembro Nº: 12.754 Nacionalidad: Sexo:	bn interesante tu solucion, Kaissa! PD: MEMORABLE el problema 1... -------------------- Empezando con Desigualdades? Encuentra aquí problemas resueltos

« Posterior · Segunda Fecha · Anterior »

2 Páginas:

< 1 2

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 25th April 2025 - 11:54 PM