C2 Álgebra y Geometría

2 Páginas:

1 2 >

C2 Álgebra y Geometría, 1S 2009

Gaston Burrull	May 26 2009, 09:36 PM Publicado: #1
Invitado	$TEX: \begin{center}<br />MAT1103 - Álgebra y Geometría\\<br />Control 2 - Martes 26 de Mayo de 2009\end{center}<br />\begin{enumerate}<br />\item Demuestre que la expresión $4^n+15n-1$ es divisible por $9$, $\forall n\in \mathbb{N}$.<br />\item Sea la sucesión de Fibonacci definida como:<br />\[ f_n= \begin{cases}<br />0 & \text{ si } n = 0 \\<br />1 & \text{ si } n = 1 \\<br />f_{n-1} + f_{n-2} & \text{ si } n > 1 \\<br />\end{cases}\]<br />Demuestre que $\displaystyle f_n\leq \left(\frac{7}{4}\right)^{n-1}.$<br /><br />\textbf{Ayuda:} Use el hecho que $\displaystyle\left(\frac{7}{4}\right)+1\leq\left(\frac{7}{4}\right)^2.$<br />\item Resuelva la siguiente sumatoria:<br />\[\sum_{i=1}^n (i-1)^2\cdot i!\]<br />\end{enumerate}<br />$

Sephiroth99 Ver Perfil del Miembro Ver los mensajes de este miembro	May 26 2009, 09:53 PM Publicado: #2
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.313 Registrado: 28-June 07 Miembro Nº: 7.123 Nacionalidad: Colegio/Liceo: Sexo:	Aqui va el 3) $TEX: $$\sum\limits_{i=1}^{n}{(i-1)^{2}i!}=\sum\limits_{i=1}^{n-1}{(i)^{2}(i+1)!}=\sum\limits_{i=1}^{n-1}{(i+3-3)\cdot (i+2-2)(i+1)!}=\sum\limits_{i=1}^{n-1}{(i+3-3)\cdot \left[ (i+2)!-2(i+1)! \right]}$$$ $TEX: $$\sum\limits_{i=1}^{n-1}{(i+3-3)\cdot \left[ (i+2)!-2(i+1)! \right]}=\sum\limits_{i=1}^{n-1}{(i+3)!-2(i+3)(i+1)!-3(i+2)!+6(i+1)!)}$$$ $TEX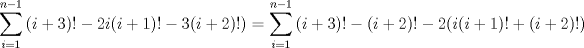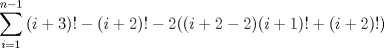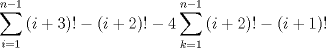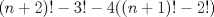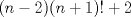: $$\sum\limits_{i=1}^{n-1}{(i+3)!-2i(i+1)!-3(i+2)!)}=\sum\limits_{i=1}^{n-1}{(i+3)!-(i+2)!-2(i(i+1)!+(i+2)!)}$$$ $TEX: $$\sum\limits_{i=1}^{n-1}{(i+3)!-(i+2)!-2((i+2-2)(i+1)!+(i+2)!)}$$$ $TEX: $$\sum\limits_{i=1}^{n-1}{(i+3)!-(i+2)!-4\sum\limits_{k=1}^{n-1}{(i+2)!-(i+1)!}}$$$ $TEX: $$(n+2)!-3!-4((n+1)!-2!)$$$ $TEX: $$(n-2)(n+1)!+2$$$ -------------------- Hay dos cosas infinitas: el Universo y la estupidez humana. Y del Universo no estoy seguro

danielomalmsteen Ver Perfil del Miembro Ver los mensajes de este miembro	May 26 2009, 10:07 PM Publicado: #3
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.413 Registrado: 13-March 08 Desde: Al frente del mundo Magico Miembro Nº: 16.846 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Aqui va el 1) $TEX: \[<br />\begin{gathered}<br /> {\text{PDQ: }}9\left\| {4^n + 15n - 1{\text{ }}\forall n \in \mathbb{N}} \right. \hfill \\<br /> \hfill \\<br /> {\text{Caso base }}n = 1{\text{ es trivial}} \hfill \\<br /> {\text{HI: Supongamos que }}4^n + 15n - 1 = 9k \hfill \\<br /> {\text{Demostremoslo para }}4^{n + 1} + 15\left( {n + 1} \right) - 1 \hfill \\<br /> 4^{n + 1} + 15\left( {n + 1} \right) - 1 = \hfill \\<br /> = 4 \cdot 4^n + 15n + 14 \hfill \\<br /> = 4 \cdot 4^n + 60n - 45n + 18 - 4 \hfill \\<br /> = 4\left( {4^n + 15n - 1} \right) + 18 - 45n \hfill \\<br /> = 4\left( {9k} \right) + 9\left( {2 - 5n} \right) \hfill \\<br /> = 9\left( {4k + 2 - 5n} \right)\square \hfill \\ <br />\end{gathered} <br />\]<br />$ xd --------------------

「Krizalid」 Ver Perfil del Miembro Ver los mensajes de este miembro	May 26 2009, 10:47 PM Publicado: #4
Staff FMAT Grupo: Super Moderador Mensajes: 8.124 Registrado: 21-May 06 Miembro Nº: 1.156 Nacionalidad: Sexo:	puedo jugar? $TEX: \begin{eqnarray}<br /> \sum\limits_{i=1}^{n}{(i-1)^{2}i!}&=&\sum\limits_{1\le i\le n}{\left( i^{2}-2i+1 \right)i!} \\ <br /> & =&\sum\limits_{1\le i\le n}{\big((i+1)(i-2)-(i-3)\big)i!} \\ <br /> & =&\sum\limits_{1\le i\le n}{\big((i-2)(i+1)!-(i-3)i!\big)} \\ <br /> & =&(n-2)(n+1)!+2. <br />\end{eqnarray}$

Gaston Burrull	May 27 2009, 10:30 PM Publicado: #5
Invitado	Bonita respuesta Krizalid. Esa pregunta nos mató a todos, creo que el único de nuestra sección en contestarla correctamente fue mi amigo cristian . Voy por la 2. Usaré el segundo principio de inducción: Sea, 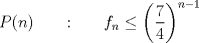$TEX: $P(n)\qquad \text{:}\qquad f_n\leq \left(\dfrac{7}{4}\right)^{n-1}$$ . Casos base: 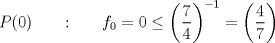$TEX: $P(0)\qquad \text{:}\qquad f_0=0\leq \left(\dfrac{7}{4}\right)^{-1}=\left(\dfrac{4}{7}\right)$$ . Verdadero. 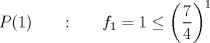$TEX: $P(1)\qquad \text{:}\qquad f_1=1\leq \left(\dfrac{7}{4}\right)^{1}$$ . Verdadero. 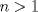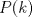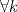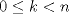Paso inductivo: Sea $TEX: $n>1$$ , asumámos $TEX: $P(k)$$ cierto $TEX: $\forall k$$ , tal que, $TEX: $0\leq k<n$$ . 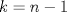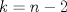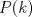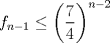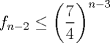Por lo que tanto tomando $TEX: $k=n-1$$ como $TEX: $k=n-2$$ se cumple $TEX: $P(k)$$ , o sea: $TEX: $f_{n-1}\leq \left(\dfrac{7}{4}\right)^{n-2}$$ $TEX: $f_{n-2}\leq \left(\dfrac{7}{4}\right)^{n-3}$$ Demostrémoslo para 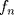$TEX: $f_{n}$$ , usando las 2 desigualdades de arriba y la ayuda del enunciado: $TEX: \begin{align}<br />f_{n}&=f_{n-1}+f_{n-2}\leq \left(\dfrac{7}{4}\right)^{n-2}+\left(\dfrac{7}{4}\right)^{n-3}=\left(\dfrac{7}{4}\right)^{n-3}\left[\left(\dfrac{7}{4}\right)+1\right]\leq \left(\dfrac{7}{4}\right)^{n-3}\left(\dfrac{7}{4}\right)^2\\<br />f_{n}&\leq\left(\dfrac{7}{4}\right)^{n-1}. \blacksquare\end{align}$

Abu-Khalil Ver Perfil del Miembro Ver los mensajes de este miembro	May 27 2009, 10:32 PM Publicado: #6
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.812 Registrado: 4-November 07 Desde: Santiago Miembro Nº: 12.213 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Eso es el Segundo Principio de Inducción. -------------------- ~milopez $TEX: \[\mathfrak{L}=\int_{-\infty}^\infty e^{-289x^2}dx=\frac{\Gamma (\frac{1}{2})}{17}=\frac{\sqrt{\pi}}{17}\]$ $TEX: <br />\begin{equation}\begin{aligned}<br />dS_t&=\mu S_t dt+\sqrt{V_t}S_t dW^S_t\\<br />dV_t&=\kappa(\theta-V_t)dt+\sigma\sqrt{V_t} dW^V_t\\<br />\end{aligned}\end{equation}<br />$ $TEX: <br />$$\mathbb A^{\text U}_M(N)$$<br />$

Gaston Burrull	May 27 2009, 10:35 PM Publicado: #7
Invitado	CITA(Abu-Khalil @ May 28 2009, 12:32 AM) Eso es el Segundo Principio de Inducción. Sí, eso puse

Abu-Khalil Ver Perfil del Miembro Ver los mensajes de este miembro	May 27 2009, 10:38 PM Publicado: #8
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.812 Registrado: 4-November 07 Desde: Santiago Miembro Nº: 12.213 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(Gaston Burrull @ May 27 2009, 11:35 PM) Sí, eso puse Bah no lo lei -------------------- ~milopez $TEX: \[\mathfrak{L}=\int_{-\infty}^\infty e^{-289x^2}dx=\frac{\Gamma (\frac{1}{2})}{17}=\frac{\sqrt{\pi}}{17}\]$ $TEX: <br />\begin{equation}\begin{aligned}<br />dS_t&=\mu S_t dt+\sqrt{V_t}S_t dW^S_t\\<br />dV_t&=\kappa(\theta-V_t)dt+\sigma\sqrt{V_t} dW^V_t\\<br />\end{aligned}\end{equation}<br />$ $TEX: <br />$$\mathbb A^{\text U}_M(N)$$<br />$

ErnestoJ Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 8 2014, 03:00 PM Publicado: #10
Principiante Matemático Grupo: Usuario FMAT Mensajes: 12 Registrado: 6-October 13 Miembro Nº: 123.055 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(Krizalid @ May 26 2009, 10:47 PM) puedo jugar? $TEX: \begin{eqnarray}<br /> \sum\limits_{i=1}^{n}{(i-1)^{2}i!}&=&\sum\limits_{1\le i\le n}{\left( i^{2}-2i+1 \right)i!} \\ <br /> & =&\sum\limits_{1\le i\le n}{\big((i+1)(i-2)-(i-3)\big)i!} \\ <br /> & =&\sum\limits_{1\le i\le n}{\big((i-2)(i+1)!-(i-3)i!\big)} \\ <br /> & =&(n-2)(n+1)!+2. <br />\end{eqnarray}$ No entiendo cómo demonios pasaste de la línea 3 a la 4. Mensaje modificado por ErnestoJ el Jan 8 2014, 03:04 PM

2 Páginas:

1 2 >

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Fecha y Hora actual: 3rd April 2025 - 04:25 PM