 Algebra lineal (sub espacio) |
|
|
|
|
|
|
Foro fmat.cl > Programa Enseñanza Universitaria > Consultas > Banco de Problemas Resueltos > Álgebra > Álgebra Lineal  |
 May 24 2009, 03:14 PM
Publicado:
#1
|
|
 Dios Matemático Supremo  Grupo: Usuario FMAT Mensajes: 1.043 Registrado: 5-February 07 Desde: EN CHILE CREO Miembro Nº: 3.980 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:   |
![TEX: % MathType!MTEF!2!1!+-<br />% feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaacaqGtb<br />% GaaeyzaiaabggacaqGGaGaaeiiaiaabweacaqGGaGaaeyzaiaabYga<br />% caqGGaGaaeyzaiaabohacaqGWbGaaeyyaiaabogacaqGPbGaae4Bai<br />% aabccacaqGKbGaaeyzaiaabccacaqG0bGaae4BaiaabsgacaqGHbGa<br />% ae4CaiaabccacaqGSbGaaeyyaiaabohacaqGGaGaaeyBaiaabggaca<br />% qG0bGaaeOCaiaabMgacaqGJbGaaeyzaiaabohacaqGGaGaaeizaiaa<br />% bwgacaqGGaGaae4BaiaabkhacaqGKbGaaeyzaiaab6gacaqGGaGaae<br />% OmaiaabIhacaqGYaGaaeiiaiaabohacaqGVbGaaeOyaiaabkhacaqG<br />% LbGaaeiiaiaabwgacaqGSbGaaeiiaiaabogacaqG1bGaaeyzaiaabk<br />% hacaqGWbGaae4BaiaabccatuuDJXwAK1uy0HMmaeHbfv3ySLgzG0uy<br />% 0HgiuD3BaGqbbiab-1risbqaaiaabofacaqGLbGaaeiiaiaabsgaca<br />% qGLbGaaeOzaiaabMgacaqGUbGaaeyzaiaab6gacaqGGaGaaeyzaiaa<br />% bYgacaqGGaGaae4CaiaabwhacaqGIbGaae4yaiaab+gacaqGUbGaae<br />% OAaiaabwhacaqGUbGaaeiDaiaab+gacaqGGaGaae4DamaaBaaaleaa<br />% caaIXaaabeaaaOqaaiaadEhadaWgaaWcbaGaaGymaaqabaGccqGH9a<br />% qpdaGadaqaamaabmaabaqbaeqabiGaaaqaaiaadIhaaeaacaWG5baa<br />% baGaamOEaaqaaiaad+gaaaaacaGLOaGaayzkaaGaai4laiaadIhaca<br />% GGSaGaamyEaiaacYcacaWG6bGaeyicI4Sae8xhHifacaGL7bGaayzF<br />% aaGaaeiiaiaab2gacaqGVbGaae4CaiaabshacaqGYbGaaeyyaiaabk<br />% hacaqGGaGaaeyCaiaabwhacaqGLbGaaeiiaiaabEhadaWgaaWcbaGa<br />% aGymaaqabaGccqGHKjYOcaWGfbaaaaa!B68D!<br />\[<br />\begin{gathered}<br /> {\text{Sea E el espacio de todas las matrices de orden 2x2 sobre el cuerpo }}\mathbb{R} \hfill \\<br /> {\text{Se definen el subconjunto w}}_1 \hfill \\<br /> w_1 = \left\{ {\left( {\begin{array}{*{20}c}<br /> x & y \\<br /> z & o \\<br /><br /> \end{array} } \right)/x,y,z \in \mathbb{R}} \right\}{\text{ mostrar que w}}_1 \leqslant E \hfill \\ <br />\end{gathered} <br />\]<br />](./tex/53defdb281fe94c3dea939125d0f175b.png) Mi duda es como demuestro usando esa matriz eso me complica :S -------------------- Contador Publico Auditor :)
|
 |
 
|
|
May 24 2009, 03:16 PM
Publicado:
#2
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.812 Registrado: 4-November 07 Desde: Santiago Miembro Nº: 12.213 Nacionalidad: Colegio/Liceo:  Universidad:  Sexo: |
¿Cuál es la base de ese subpespacio? Fijate que depende de 3 constantes.
-------------------- |
|
|
|
![TEX: \[\mathfrak{L}=\int_{-\infty}^\infty e^{-289x^2}dx=\frac{\Gamma (\frac{1}{2})}{17}=\frac{\sqrt{\pi}}{17}\]](./tex/e0e88dba678ca3ead120b088f41191b2.png)
|
May 24 2009, 03:19 PM
Publicado:
#3
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.818 Registrado: 21-December 06 Miembro Nº: 3.434 |
Es claro que la matriz nula pertenece a ese conjunto.
Ahora, si sumas 2 matrices de ese conjunto, que te queda? Y finalmente, que pasa si multiplicas una matriz de ese conjunto por un escalar? Recuerda que sólo tienes que verificar que el conjunto es cerrado bajos esas operaciones, es decir, que si sumas 2 matrices de esa forma (que el elemento 2,2 sea 0) entonces la suma debe tener el elemento 2,2 igual a 0 también. Lo mismo para multiplicación por escalar. -------------------- |
|
|
|
|
Mar 30 2010, 06:31 PM
Publicado:
#4
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 247 Registrado: 11-December 08 Miembro Nº: 40.674 Nacionalidad: Colegio/Liceo:  Universidad:  Sexo: |
CITA(DressedToKill @ May 24 2009, 05:19 PM)  Es claro que la matriz nula pertenece a ese conjunto. Ahora, si sumas 2 matrices de ese conjunto, que te queda? Y finalmente, que pasa si multiplicas una matriz de ese conjunto por un escalar? Recuerda que sólo tienes que verificar que el conjunto es cerrado bajos esas operaciones, es decir, que si sumas 2 matrices de esa forma (que el elemento 2,2 sea 0) entonces la suma debe tener el elemento 2,2 igual a 0 también. Lo mismo para multiplicación por escalar. Con eso demuestras que es subespacio de V. Si es subespacio, tienes que 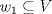 . Como relacionamos esto a la desigualdad  ?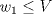
|
|
|
|
|
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 6th March 2025 - 09:37 PM |
