Sobre cuadrados perfectos - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Sector Preparación Olimpiadas > Sector Olímpico > Teoría de Números > Problemas Resueltos

Reply to this topic

Start new topic

Sobre cuadrados perfectos

coquitao Ver Perfil del Miembro Ver los mensajes de este miembro	May 12 2009, 12:30 AM Publicado: #1
Dios Matemático Supremo Grupo: Super Moderador Mensajes: 2.065 Registrado: 25-May 08 Desde: Pelotillehue Miembro Nº: 24.463	¿Existirá una infinidad de tercias (x,y,z) 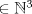$TEX: $\in \mathbb{N}^{3}$$ tales que x, y y z están en progresión aritmética y los números xy+1, yz+1 y zx+1 son cuadrados perfectos? Espero sus soluciones. -------------------- "Please forget everything you have learned in school; for you haven't learned it... Please keep in mind at all times the corresponding portions of your school curriculum; for you haven't actually forgotten them." -- E. Landau

tochalo Ver Perfil del Miembro Ver los mensajes de este miembro	Mar 18 2011, 10:42 AM Publicado: #2
Dios Matemático Grupo: Usuario FMAT Mensajes: 426 Registrado: 13-January 08 Desde: desde la pieza de tu hermana Miembro Nº: 14.612 Nacionalidad: Colegio/Liceo: Sexo:	Ahora puedo morir en paz xD $TEX: \noindent<br />Sea el par $(r,s)$ solución de la ecuación de Pell $x^2-3y^2=1$. Luego la terna $(2s-r,2s,2s+r)$ satisface las condiciones del problema. En efecto, dicha terna es una progresión aritmética de diferencia $r$, la cual cumple que<br />\begin{eqnarray}<br />(2s-r)2s+1&=&(s-r)^2\\<br />(2s+r)2s+1&=&(s+r)^2\\<br />(2s-r)(2s+r)+1&=&s^2<br />\end{eqnarray}<br />La infinitud de las ternas se sigue de la infinitud de las soluciones de la ecuación de Pell.\\<br />Por ejemplo, el par (7,4) nos da la terna (1,8,15), la cual fue expuesta por Coquitao, arbiter elegantiae.<br />otras soluciones son (4,30,56) y (15,112,209).<br />$ Saludos, mi estimado

coquitao Ver Perfil del Miembro Ver los mensajes de este miembro	Mar 23 2011, 11:48 AM Publicado: #3
Dios Matemático Supremo Grupo: Super Moderador Mensajes: 2.065 Registrado: 25-May 08 Desde: Pelotillehue Miembro Nº: 24.463	Muy buena, tochalo... Sigue así. He aquí una ilustración más del argumento empleado por tochalo (ya saben, hay que buscar siempre las analogías): http://www.fmat.cl/index.php?showtopic=60975&hl= -------------------- "Please forget everything you have learned in school; for you haven't learned it... Please keep in mind at all times the corresponding portions of your school curriculum; for you haven't actually forgotten them." -- E. Landau

« Posterior · Problemas Resueltos · Anterior »

Reply to this topic

Start new topic

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 3rd April 2025 - 04:56 PM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.