Desigualdad de Bernoulli - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Programa Enseñanza Universitaria > Ejercitación > Álgebra > Desigualdades e Inecuaciones

Reply to this topic

Start new topic

Desigualdad de Bernoulli, Probar con Inducción

user2 Ver Perfil del Miembro Ver los mensajes de este miembro	May 7 2008, 10:34 AM Publicado: #1
Matemático Grupo: Usuario FMAT Mensajes: 53 Registrado: 2-May 08 Miembro Nº: 21.954	$TEX: \[<br />\forall a > - 1,\quad \forall n,\quad (1 + a)^n \geqslant 1 + na<br />\]<br />$ Quién me ayuda??????

Aprendixmat Ver Perfil del Miembro Ver los mensajes de este miembro	May 24 2008, 12:58 PM Publicado: #2
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 512 Registrado: 28-November 06 Miembro Nº: 3.014 Nacionalidad: Universidad: Sexo:	No se si aun te sirva pero aquí va.. $TEX: Si n=1 la desigualdad es trivial<br />\\<br />\\<br />\underline{Hipotesis de inducci\'on}: Supongamos que la desigualdad se cumple para $n=k$ es decir , $(1+a)^k\ge 1+ka$ cuando $a>-1$<br />\\<br />\\<br />\underline{Por demostrar}: Si $n=k+1$ se verifica que $$(1+a)^{k+1}\ge 1+(k+1)a.$$ <br />\\<br />\underline{Demostraci\'on}: Por hipotesis de inducci\'on $$(1+a)^k\ge 1+ka$$ multiplicando ambos miembros de la desigualdad por $a+1>0$ tenemos que $$(1+a)^{k+1}\ge (1+a)(1+ka)=1+ka+a+ka^2.$$ Ahora bien , como $$ka^2\ge 0$$ entonces $$1+ka+a+ka^2\ge 1+ka+a=1+(k+1)a$$luego por transitividad $$(1+a)^{k+1}\ge 1+(k+1)a.$$ $$Q.E.D$$$ saludos .

zazon Ver Perfil del Miembro Ver los mensajes de este miembro	May 5 2009, 05:10 PM Publicado: #3
Principiante Matemático Grupo: Usuario FMAT Mensajes: 8 Registrado: 15-March 08 Desde: Arica Miembro Nº: 16.972 Nacionalidad: Universidad: Sexo:	CITA(Aprendixmat @ May 24 2008, 02:58 PM) No se si aun te sirva pero aquí va.. $TEX: Si n=1 la desigualdad es trivial<br />\\<br />\\<br />\underline{Hipotesis de inducci\'on}: Supongamos que la desigualdad se cumple para $n=k$ es decir , $(1+a)^k\ge 1+ka$ cuando $a>-1$<br />\\<br />\\<br />\underline{Por demostrar}: Si $n=k+1$ se verifica que $$(1+a)^{k+1}\ge 1+(k+1)a.$$ <br />\\<br />\underline{Demostraci\'on}: Por hipotesis de inducci\'on $$(1+a)^k\ge 1+ka$$ multiplicando ambos miembros de la desigualdad por $a+1>0$ tenemos que $$(1+a)^{k+1}\ge (1+a)(1+ka)=1+ka+a+ka^2.$$ Ahora bien , como $$ka^2\ge 0$$ entonces $$1+ka+a+ka^2\ge 1+ka+a=1+(k+1)a$$luego por transitividad $$(1+a)^{k+1}\ge 1+(k+1)a.$$ $$Q.E.D$$$ hola Aprendixmat me gustaria preguntar de donde deduciste que ka^2=0 , disculpa la ignorancia , siempre se me van algunos detalles aunque me serviria que describieras detalladamente (si no es mucha molestia) el procedimiento Mensaje modificado por zazon el May 5 2009, 05:11 PM

snw Ver Perfil del Miembro Ver los mensajes de este miembro	May 5 2009, 05:17 PM Publicado: #4
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.139 Registrado: 11-June 08 Desde: UK Miembro Nº: 26.837 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(zazon @ May 5 2009, 07:10 PM) hola Aprendixmat me gustaria preguntar de donde deduciste que ka^2=0 , disculpa la ignorancia , siempre se me van algunos detalles aunque me serviria que describieras detalladamente (si no es mucha molestia) el procedimiento lo que se dedujo es que 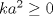$TEX: $ka^2\ge 0$$ por lo tanto la desigualdad era menor, es como : $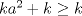TEX: $ka^2+k\ge k$$ -------------------- blep

coquitao Ver Perfil del Miembro Ver los mensajes de este miembro	May 9 2009, 07:16 PM Publicado: #5
Dios Matemático Supremo Grupo: Super Moderador Mensajes: 2.065 Registrado: 25-May 08 Desde: Pelotillehue Miembro Nº: 24.463	Solución alternativa. Si 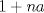$TEX: $1+na$$ es menor o igual a cero no hay nada que hacer, pues el lado izquierdo de la inecuación siempre es estrictamente mayor que cero. En caso contrario, aplica la desigualdad entre la media geométrica y la media aritmética a los siguientes 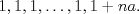$TEX: $n$$ números: $TEX: $1,1,1,\ldots, 1,1+na.$$ Queda: $TEX: $\displaystyle \sqrt[n]{1+na} = \sqrt[n]{(1)(1)\cdots (1)(1+na)} \leq \frac{(n-1)+(1+na)}{n} = 1+a$$ y de ahí el resultado. -------------------- "Please forget everything you have learned in school; for you haven't learned it... Please keep in mind at all times the corresponding portions of your school curriculum; for you haven't actually forgotten them." -- E. Landau

« Posterior · Desigualdades e Inecuaciones · Anterior »

Reply to this topic

Start new topic

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Versión Lo-Fi

Fecha y Hora actual: 28th April 2025 - 03:54 PM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.