|
|
|
|
|
|
|
  |
 May 1 2009, 02:18 PM May 1 2009, 02:18 PM
Publicado:
#1
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.564 Registrado: 12-November 07 Desde: La Union, XIV Region de los Rios Miembro Nº: 12.607 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Sean
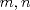 enteros positivos tales que enteros positivos tales que  divide a divide a 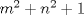 . Probar que: . Probar que: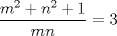 Hint: Mensaje modificado por Kain #13 el Jun 1 2009, 05:25 PM -------------------- Ricardo Vargas Obando
Ex-alumno Deutsche Schule La Unión (Generación 2010, de los 150 años). Novato de Licenciatura en Matemática/Estadística, en la Pontificia Universidad Católica de Chile.  Grupo de facebook de Novatos Matemática y Estadística PUC 2011 Currículum Olímpico:
|
|
|
|
 May 29 2009, 10:42 PM May 29 2009, 10:42 PM
Publicado:
#2
|
|
 Puntaje Nacional PSU Matemáticas Admisión 2010 Grupo: Colaborador Gold Mensajes: 390 Registrado: 22-July 07 Desde: la granja Miembro Nº: 7.754 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Notar que si
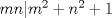 entonces entonces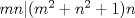 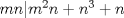 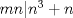 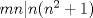 Aquí hay dos casos: 1) 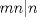 => => 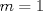 luego reemplazando en la expresión orgininal 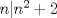 => => 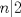 , por tanto , por tanto 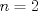 Ahora 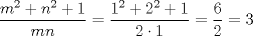 Comprobando lo pedido 2) 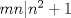 => => 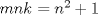 esto es esto es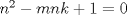 Luego sean 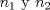 las raices de la ecucación, podemos ver que las raices de la ecucación, podemos ver que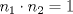 y como n es entero positivo, 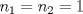 Luego 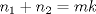 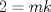 Entonces 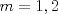 Se nos forman dos pares m,n 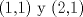 Ya vimos que el par (2,1) me da el valor tres de le expresión, ahora veamos el (1,1) 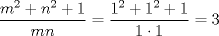 Comprobando lo pedido -------------------- ...
|
|
|
|
 May 29 2009, 10:58 PM May 29 2009, 10:58 PM
Publicado:
#3
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.139 Registrado: 11-June 08 Desde: UK Miembro Nº: 26.837 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Notar que si 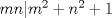 entonces entonces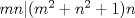 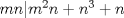 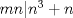 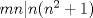 Aquí hay dos casos: 1) 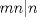 => => 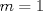 luego reemplazando en la expresión orgininal ese paso lo encuentro cuestionable, por ejemplo 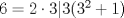 pero no se cumple lo que tu pusiste pero no se cumple lo que tu pusistesaludos -------------------- blep
|
|
|
|
 May 30 2009, 06:22 PM May 30 2009, 06:22 PM
Publicado:
#4
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.564 Registrado: 12-November 07 Desde: La Union, XIV Region de los Rios Miembro Nº: 12.607 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Tal como señalo el Matias, la solucion es incorrecta
Tu señalas que  divide a divide a 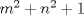 => =>  divide a divide a 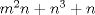 , pero el reciproco de esta implicancia no es siempre correcto (como podemos ver en el ejemplo de Matias). , pero el reciproco de esta implicancia no es siempre correcto (como podemos ver en el ejemplo de Matias).Saludos, y a seguir trabajando -------------------- Ricardo Vargas Obando
Ex-alumno Deutsche Schule La Unión (Generación 2010, de los 150 años). Novato de Licenciatura en Matemática/Estadística, en la Pontificia Universidad Católica de Chile.  Grupo de facebook de Novatos Matemática y Estadística PUC 2011 Currículum Olímpico:
|
|
|
|
 May 30 2009, 09:18 PM May 30 2009, 09:18 PM
Publicado:
#5
|
|
 Puntaje Nacional PSU Matemáticas Admisión 2010 Grupo: Colaborador Gold Mensajes: 390 Registrado: 22-July 07 Desde: la granja Miembro Nº: 7.754 Nacionalidad:  Colegio/Liceo:  Sexo:  |
aaa, me confundi al aplicar que si
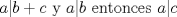 Luego de ahí se tiene que 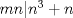 Pero al hacer esto, asumo que si 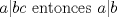 cosa q no siempre se cumple cosa q no siempre se cumple-------------------- ...
|
|
|
|
 Jun 1 2009, 05:20 PM Jun 1 2009, 05:20 PM
Publicado:
#6
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.139 Registrado: 11-June 08 Desde: UK Miembro Nº: 26.837 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
hay un método que se utiliza comúnmente para hacer este tipo de "clásicos" IMO, se llama algo asi "vieta jumping" aunque no he visto la solución de este problema, hay muchos parecidos que se hacen con esto.
saludos, si encuentro la solución la posteo, pero por lo meno busquen algo acerca de este método que es bastante útil -------------------- blep
|
|
|
|
 Jun 1 2009, 09:04 PM Jun 1 2009, 09:04 PM
Publicado:
#7
|
|
 Principiante Matemático Destacado Grupo: Usuario FMAT Mensajes: 26 Registrado: 1-November 08 Desde: Santiago de Chile Miembro Nº: 37.535 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Tomando las recomendaciones...
Sea 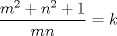 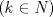 Se fija Se fija 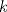 y se consideran todos los pares y se consideran todos los pares 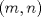 que satisfagan la ecuación es decir: que satisfagan la ecuación es decir: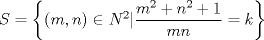 Sea 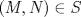 un para que minimize la suma un para que minimize la suma  . Sin pérdida de la generalidad asumamos que . Sin pérdida de la generalidad asumamos que 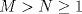 Luego consideremos la ecuación: Luego consideremos la ecuación: 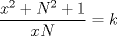 es decir es decir 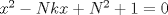 Notar que una de las raíces de la ecuación es 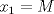 la otra se obtiene por las relaciones de las raíces de la ecuación cuadrática es decir la otra se obtiene por las relaciones de las raíces de la ecuación cuadrática es decir 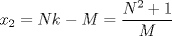 lo que implica que lo que implica que 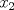 es un número natural. es un número natural. Luego por que 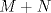 es un mínimo concluimos que es un mínimo concluimos que 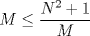 Lo cual implica que: 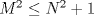 Pero como Pero como 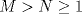 implica que implica que 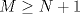 luego luego 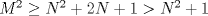 Lo cual es una contradicción. Lo cual es una contradicción.Entonces  y luego tenemos que: y luego tenemos que: 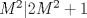 . De aquí se concluye que . De aquí se concluye que 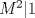 y entonces y entonces 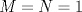 . Lo cual cumple que: . Lo cual cumple que: 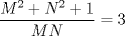 PD: Me pareció muy buena esa técnica del "Vieta Jumping" -------------------- Aquiles Esquivel Medrazo
Estudiante Cursando 7º Básico |
|
|
|
 Jun 1 2009, 10:57 PM Jun 1 2009, 10:57 PM
Publicado:
#8
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.139 Registrado: 11-June 08 Desde: UK Miembro Nº: 26.837 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Tomando las recomendaciones... Sea 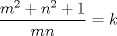 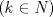 Se fija Se fija 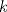 y se consideran todos los pares y se consideran todos los pares 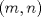 que satisfagan la ecuación es decir: que satisfagan la ecuación es decir: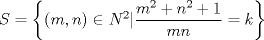 Sea 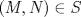 un para que minimize la suma un para que minimize la suma  . Sin pérdida de la generalidad asumamos que . Sin pérdida de la generalidad asumamos que 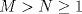 Luego consideremos la ecuación: Luego consideremos la ecuación: 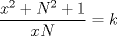 es decir es decir 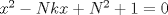 Notar que una de las raíces de la ecuación es 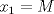 la otra se obtiene por las relaciones de las raíces de la ecuación cuadrática es decir la otra se obtiene por las relaciones de las raíces de la ecuación cuadrática es decir 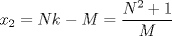 lo que implica que lo que implica que 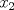 es un número natural. es un número natural. Luego por que 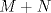 es un mínimo concluimos que es un mínimo concluimos que 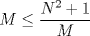 Lo cual implica que: 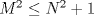 Pero como Pero como 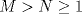 implica que implica que 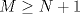 luego luego 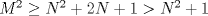 Lo cual es una contradicción. Lo cual es una contradicción.Entonces  y luego tenemos que: y luego tenemos que: 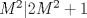 . De aquí se concluye que . De aquí se concluye que 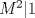 y entonces y entonces 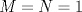 . Lo cual cumple que: . Lo cual cumple que: 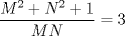 PD: Me pareció muy buena esa técnica del "Vieta Jumping" la solución es correcta pero al final justificaría por que m^2|1, lo cual es claro porque 2m^2+1 es coprimo con m^2 pero hay que convencer a los incrédulos saludos -------------------- blep
|
|
|
|
 Jun 9 2009, 06:04 PM Jun 9 2009, 06:04 PM
Publicado:
#9
|
|
 Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 193 Registrado: 22-March 07 Desde: San Miguel, Santiago Miembro Nº: 4.651 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
al qe le interese mas esta tecnica hay un pdf en una pagina qe se llama mathematical reflections, el link es el siguiente http://reflections.awesomemath.org/2007_5/vieta_jumping.pdf, la solucion mostrada es bastante similar a la del pdf... me gustaria recalcar qe aparece un problema de la imo de 2007 en vietnam a la cual me toco ir y no me salio hahaha no sabia esta tecnica... pero en fin, nunca es tarde para aprender
-------------------- |
|
|
|
 Feb 7 2011, 11:27 AM Feb 7 2011, 11:27 AM
Publicado:
#10
|
|
|
Matemático Grupo: Usuario FMAT Mensajes: 61 Registrado: 8-May 10 Miembro Nº: 70.464 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Estaba mirando este problema y me di cuenta qe esta malo solo un ejemplo (m,n)=(2,1) cumple, entonces no implica que m=n, por lo tanto la respuesta expuesta esta mala, la verdadera respuesta son (1,1) y
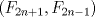 sonde F_k es el k-esimo término de la sucecion de fibonacci, los cuales cumplen que sonde F_k es el k-esimo término de la sucecion de fibonacci, los cuales cumplen que 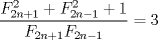
|
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 3rd April 2025 - 04:55 PM |










