Dimensión - Foro fmat.cl

Dimensión, Uno a bote pronto

coquitao Ver Perfil del Miembro Ver los mensajes de este miembro	Apr 2 2009, 01:13 PM Publicado: #1
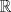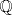Dios Matemático Supremo Grupo: Super Moderador Mensajes: 2.065 Registrado: 25-May 08 Desde: Pelotillehue Miembro Nº: 24.463	¿Cuál es la dimensión de $TEX: $\mathbb{R}$$ como espacio vectorial sobre $TEX: $\mathbb{Q}$$ ? Saludos. -------------------- "Please forget everything you have learned in school; for you haven't learned it... Please keep in mind at all times the corresponding portions of your school curriculum; for you haven't actually forgotten them." -- E. Landau

Respuestas

coquitao Ver Perfil del Miembro Ver los mensajes de este miembro	Mar 24 2010, 10:21 PM Publicado: #2
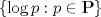Dios Matemático Supremo Grupo: Super Moderador Mensajes: 2.065 Registrado: 25-May 08 Desde: Pelotillehue Miembro Nº: 24.463	Denotemos con P al conjunto de números primos (positivos). 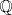Una alternativa de solución más consiste en emplear el TFA para demostrar que el conjunto $TEX: $\{\log p: p \in \mathbf{P} \}$$ es un subconjunto linealmente independiente de los reales (considerando que el campo subyacente al espacio es $TEX: $\mathbb{Q}$$ ). Así, de la infinitud de P se tendría que el grado de la extensión $TEX: $[\mathbb{R}: \mathbb{Q}]$$ no puede ser finito. QED. -------------------- "Please forget everything you have learned in school; for you haven't learned it... Please keep in mind at all times the corresponding portions of your school curriculum; for you haven't actually forgotten them." -- E. Landau

Mensajes en este tema

coquitao Dimensión Apr 2 2009, 01:13 PM

DressedToKill Es infinito. La forma usual de demostrarlo (supon... Nov 7 2009, 05:53 PM

coquitao Buena, [color=#A0522D]Dressed. Igual se puede mejo... Nov 7 2009, 06:07 PM

Kaissa $ $\\ Lema 1: Existen n\... Nov 7 2009, 08:09 PM

coquitao Y bien, he ahí una solución más. Muy buena, Kaissa... Nov 7 2009, 08:47 PM

daglnn0x0 Más simple aún; si $\mathbb{R}$ tu... Nov 19 2009, 10:08 AM

coquitao Más simple aún; si $\mathbb{R}$ tu... Dec 4 2009, 01:25 AM

coquitao Denotemos con P al conjunto de números primos (pos... Mar 24 2010, 10:21 PM

2 usuario(s) está(n) leyendo esta discusión (2 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Fecha y Hora actual: 7th April 2025 - 10:13 AM