 ayuda con demostracion |
|
|
|
|
|
|
Foro fmat.cl > Programa Enseñanza Universitaria > Consultas > Banco de Problemas Resueltos > Cálculo > Axiomas de Orden y Cuerpo  |
 Mar 30 2009, 03:24 PM
Publicado:
#1
|
|
 Doctor en Matemáticas  Grupo: Usuario FMAT Mensajes: 198 Registrado: 18-March 08 Desde: mi casa :P Miembro Nº: 17.225 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:   |
para todo x ey q pertenecen a los reales x<-1 y (conectivo) y >-1 implica x/(1+x) > y/(1+y)
|
 |
 
|
|
Mar 31 2009, 12:58 AM
Publicado:
#2
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 554 Registrado: 3-July 08 Desde: ... desde los pastos??? Miembro Nº: 28.965 Nacionalidad: Universidad:  Sexo: |
CITA(Mario_25 @ Mar 30 2009, 03:24 PM)  para todo x ey q pertenecen a los reales x<-1 y (conectivo) y >-1 implica x/(1+x) > y/(1+y) lo mismo pero en latex: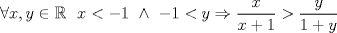 
-------------------- Si haces consultas, por lo menos lee las reglas del sitio...    Antes de ponerte a estudiar ¿Quieres un rico mate? Prepáralo con Hierba de Gauss |
|
|
|
|
Jan 15 2010, 12:21 AM
Publicado:
#3
|
|
 Staff FMAT  Grupo: Super Moderador Mensajes: 4.857 Registrado: 2-January 08 Miembro Nº: 14.268 Nacionalidad: Colegio/Liceo:  Universidad:  Sexo: |
![TEX: % MathType!MTEF!2!1!+-<br />% feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaadaqjEa<br />% qaaiaabseacaqGLbGaaeyBaiaab+gacaqGZbGaaeiDaiaabkhacaqG<br />% HbGaae4yaiaabMgacaqGVbGaaeOBaiaabccacaqG6aaaaaqaaiaabc<br />% facaqGVbGaaeOCaiaabccacaqGObGaaeyAaiaabchacaqGVbGaaeiD<br />% aiaabwgacaqGZbGaaeyAaiaabohacaqGGaGaae4CaiaabwgacaqGGa<br />% GaaeiDaiaabMgacaqGLbGaaeOBaiaabwgacaqGGaGaaeyCaiaabwha<br />% caqGLbGaaeiiaiaabccacaWG4bGaey4kaSIaaGymaiabgYda8iaaic<br />% dacaqGGaGaaeyzaiaabccacaqGGaGaamyEaiabgUcaRiaaigdacqGH<br />% +aGpcaaIWaGaaeilaiaabccacaqGKbGaaeyzaiaabccacaqGSbGaae<br />% 4BaiaabccacaqGHbGaaeOBaiaabshacaqGLbGaaeOCaiaabMgacaqG<br />% VbGaaeOCaiaabccacaqGZbGaaeyzaiaabccacaqGZbGaaeyAaiaabE<br />% gacaqG1bGaaeyzaiaabccacaqGXbGaaeyDaiaabwgacaqGGaGaaeii<br />% aiabgkHiTiaadIhacqGHsislcaaIXaGaeyicI4SaeSyhHe6aaWbaaS<br />% qabeaacqGHRaWkaaGccaGGSaaabaGaamyEaiabgUcaRiaaigdacqGH<br />% iiIZcqWIDesOdaahaaWcbeqaaiabgUcaRaaakiaabYcacaqGGaGaae<br />% iCaiaab+gacaqGYbGaaeiiaiaabshacaqGHbGaaeOBaiaabshacaqG<br />% VbGaaeiiaiaabccacaWG5bGaey4kaSIaaGymaiabgkHiTiaadIhacq<br />% GHsislcaaIXaGaeyicI4SaeSyhHe6aaWbaaSqabeaacqGHRaWkaaGc<br />% caqGGaGaaeizaiaabwgacaqGGaGaaeizaiaab+gacaqGUbGaaeizai<br />% aabwgacaqGGaGaaeiiaiaadMhacqGHsislcaWG4bGaeyicI4SaeSyh<br />% He6aaWbaaSqabeaacqGHRaWkaaGccaqGSaGaaeiiaiaabwgacaqGZb<br />% GaaeiiaiaabsgacaqGLbGaae4yaiaabMgacaqGYbGaaeiiaiaabcca<br />% caWG5bGaeyOpa4JaamiEaiaac6caaeaaaeaacaqGqbGaae4Baiaabk<br />% hacaqGGaGaae4yaiaab+gacaqGUbGaae4CaiaabMgacaqGNbGaaeyD<br />% aiaabMgacaqGLbGaaeOBaiaabshacaqGLbGaaeOoaiaabccacaqGGa<br />% GaamiEaiabgUcaRiaadIhacaWG5bGaeyipaWJaamiEaiaadMhacqGH<br />% RaWkcaWG5bGaeyi1HS9aaSaaaeaacaWG4bGaey4kaSIaamiEaiaadM<br />% haaeaacaWG4bGaey4kaSIaaGymaaaacqGH+aGpcaWG5bGaeyi1HS9a<br />% aSaaaeaacaWG4bWaaeWaaeaacaaIXaGaey4kaSIaamyEaaGaayjkai<br />% aawMcaaaqaaiaadIhacqGHRaWkcaaIXaaaaiabg6da+iaadMhacqGH<br />% uhY2daWcaaqaaiaadIhaaeaacaWG4bGaey4kaSIaaGymaaaacqGH+a<br />% GpdaWcaaqaaiaadMhaaeaacaWG5bGaey4kaSIaaGymaaaacaGGUaaa<br />% baaabaGaaeyuaiaab6cacaqGLbGaaeOlaiaabsgaaaaa!01E8!<br />\[<br />\begin{gathered}<br /> \boxed{{\text{Demostracion :}}} \hfill \\<br /> {\text{Por hipotesis se tiene que }}x + 1 < 0{\text{ e }}y + 1 > 0,{\text{ de lo anterior se sigue que }} - x - 1 \in \mathbb{R}^ + , \hfill \\<br /> y + 1 \in \mathbb{R}^ + {\text{, por tanto }}y + 1 - x - 1 \in \mathbb{R}^ + {\text{ de donde }}y - x \in \mathbb{R}^ + {\text{, es decir }}y > x. \hfill \\<br /> \hfill \\<br /> {\text{Por consiguiente: }}x + xy < xy + y \Leftrightarrow \frac{{x + xy}}<br />{{x + 1}} > y \Leftrightarrow \frac{{x\left( {1 + y} \right)}}<br />{{x + 1}} > y \Leftrightarrow \frac{x}<br />{{x + 1}} > \frac{y}<br />{{y + 1}}. \hfill \\<br /> \hfill \\<br /> {\text{Q}}{\text{.e}}{\text{.d}} \hfill \\ <br />\end{gathered} <br />\]](./tex/6619f5d2989109dc5c125fcbed503383.png) -------------------- Candidato a doctor en Cs. De la ingeniería mención modelamiento matemático, DIM. Universidad de Chile
Magíster en ciencias mención matemática, Profesor de estado en matemáticas y computación, Licenciado en educación matemáticas y computación, USACH |
|
|
|
|
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 18th February 2025 - 04:58 PM |
