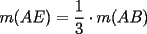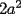|
|
|
|
|
|
|
  |
 Aug 8 2005, 10:29 AM Aug 8 2005, 10:29 AM
Publicado:
#1
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
La prueba por equipos en esta ocasión, trata sobre construcciones geométricas. Ya hubo una similar el año pasado, donde podíamos usar regla y compás. Habitualmente las construcciones geométricas se estudian con esas dos herramientas, pero... ¿Si no tuviénramos compás? La respuesta está en la siguiente prueba por equipos, pero nuestra regla es "especial"
Prueba por equipos, todos los niveles 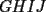 , como el que muestra la figura. , como el que muestra la figura. screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img249.imageshack.us/img249/897/regladedibujo8cx.jpg');}" /> screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img249.imageshack.us/img249/897/regladedibujo8cx.jpg');}" />Consideremos ahora una regla, sin ningún tipo de medida, en la cual sólo sabemos que los bordes 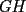 e e 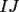 son rectos y paralelos. El ancho de la regla (o sea la distancia entre los bordes paralelos) es igual a son rectos y paralelos. El ancho de la regla (o sea la distancia entre los bordes paralelos) es igual a 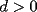 . La siguiente figura muestra esta regla especial: . La siguiente figura muestra esta regla especial: screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img246.imageshack.us/img246/5323/reglaespecial2ps.jpg');}" /> screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img246.imageshack.us/img246/5323/reglaespecial2ps.jpg');}" />Nota: los ángulos 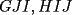 no son necesariamente rectos. Además no se permite doblar ni hacer marcas en la regla. Puede considerar que la regla tiene un largo suficiente como para marcar cualquier trazo que se necesite. no son necesariamente rectos. Además no se permite doblar ni hacer marcas en la regla. Puede considerar que la regla tiene un largo suficiente como para marcar cualquier trazo que se necesite.Además, dado un trazo 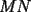 , denotaremos por , denotaremos por 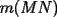 su longitud (o sea la medida del trazo su longitud (o sea la medida del trazo 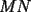 ) )Utilizando esta regla especial, y solamente ella, se pide realizar las siguientes construcciones geométricas: dado un trazo 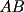 , con , con 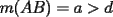 : :
Conviene tener en cuenta qué cosas se pueden hacer, y qué cosas NO se pueden hacer. Con una regla de dibujo pueden hacerse ángulos rectos de manera muy sencilla, ocupando los bordes. Esto NO se permite con la regla especial, porque no tenemos una idea sobre la forma de los bordes 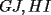 . También se prohíbe doblar o hacer marcas en la regla, porque eso tiene relación con recordar la medida de un segmento (al menos cuando se trata de construcciones matemáticas). Normalmente es el compás el que se usa para ese fin. El ancho constante de la regla, puede aprovecharse para dibujar rectas paralelas, pero dichas rectas quedan siempre a distancia . También se prohíbe doblar o hacer marcas en la regla, porque eso tiene relación con recordar la medida de un segmento (al menos cuando se trata de construcciones matemáticas). Normalmente es el compás el que se usa para ese fin. El ancho constante de la regla, puede aprovecharse para dibujar rectas paralelas, pero dichas rectas quedan siempre a distancia 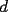 . Observamos que NO es cualquier paralela. . Observamos que NO es cualquier paralela.1º medio: 1, 2, 3, 5, 7 2º medio: 1, 2, 4, 6, 7 3º medio: 1, 4, 8, 9, 10 4º medio: 1, 4, 8, 11, 12 -------------------- |
|
|
|
 Aug 8 2005, 04:47 PM Aug 8 2005, 04:47 PM
Publicado:
#2
|
|
|
Matemático Grupo: Usuario FMAT Mensajes: 34 Registrado: 6-August 05 Desde: some place pwning noobs Miembro Nº: 167 |
si alguien tiene otra solucion porfavor posteenlo
(1) paso1: marcar punto A y B y trazar la recta paso2: sabemos con certeza que la regla que ocupamos tiene dos lados paralelos, con ellos inclinamos la regla ( como d < a ) para trazar dos paralela que pase por A y B paso3: tomando la paralela que pasa por B como y guia trazamos otra paralela usando el ancho "d" de la regla , el punto donde corta la tercera recta con la recta AB sera el punto C espero que me entiendan XD! -------------------- |
|
|
|
 Aug 8 2005, 05:45 PM Aug 8 2005, 05:45 PM
Publicado:
#3
|
|
|
Matemático Grupo: Usuario FMAT Mensajes: 34 Registrado: 6-August 05 Desde: some place pwning noobs Miembro Nº: 167 |
(2)
Bueno aqui es silimar al ejercicio (1), lo que hacemos es repeter el proceso de encontrar el punto C, una vez ubicado los puntos trazamos paralelas hacia el "otro lado" y los punto donde se cortan las dos paralelas exteriores de forma vertical trazamos una recta (eso puntos marcado con azul) y ya tenemos una recta perpendicular al a recata AB en el punto B [si no se convencen, traten de comprobar que los dos puntos azules + los puntos A y C forma un rombo 
-------------------- |
|
|
|
 Aug 8 2005, 06:02 PM Aug 8 2005, 06:02 PM
Publicado:
#4
|
|
|
Matemático Grupo: Usuario FMAT Mensajes: 34 Registrado: 6-August 05 Desde: some place pwning noobs Miembro Nº: 167 |
(3) y (4)
nuevamente similar al caso anterior una vez hecho las paralelas que pasa por los puntos A y B lo trazamos hacia el oto lado tb, al unir los puntos donde se intercectan las rectas paralelas de de forma vertical tenemos la simetral del trazo AB es ovbio decir que la simetral de un trazo cortan en ella en el punto medio 
-------------------- |
|
|
|
 Aug 8 2005, 10:35 PM Aug 8 2005, 10:35 PM
Publicado:
#5
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
En cuanto a las justificaciones, el 1 está correcto por teorema de Thales: al ser las paralelas equidistantes, esos dos segmentos miden lo mismo. Para los problemas del 2 al 4, es sencillo entender que formamos un paralelógramo. Para ver que es un rombo, cosa de fijarse que el triángulo superior (mirando el problema 4) y ver que es isósceles. Eso ocurre porque las rectas oblicuas tienen la misma inclinación. Si llamamos F al punto de arriba, tenemos que los ángulos ABF y BAF son iguales
Conozco una solución adicional para los problemas 1 y 4, que presentaré en su debido momento... primero deben responder las otras preguntas -------------------- |
|
|
|
 Aug 9 2005, 03:39 PM Aug 9 2005, 03:39 PM
Publicado:
#6
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 257 Registrado: 16-May 05 Desde: mmm perdio xD Miembro Nº: 34 Nacionalidad:  Colegio/Liceo:  Sexo:  |
mmmmm en esta parte de la fecha, la grupal tuvimos varios problemas......
Bueno .... es que nunca entendimos que las rectas las poniamos nosotros o tenia que estar buena en todos los ángulos en la recta.. aparte si nos salia en un solo caso, y por casualidad y luego lo probabamos con otro ángulo.... bueno eso.... -------------------- Trabajando en una nueva firma...
|
|
|
|
 Aug 9 2005, 04:10 PM Aug 9 2005, 04:10 PM
Publicado:
#7
|
|
|
Principiante Matemático Grupo: Usuario FMAT Mensajes: 4 Registrado: 8-August 05 Desde: Santiago Miembro Nº: 198 |
aaa...en esa prueba por ekipos...creo que al ver la prueba todos pensaban aa que facil...pero luego al pasar el rato...se empezo a ver un jugoseo extremo...= pudimos hacer dos de ellos...pero los otros ..salian respuestan totalemente nada que ver con lo que he visto aca...bueno....de acuerdo con SoLiD_UsHeR....esa fecha jajaaj fue como ....¬¬!...
ya..eso.. adios! tengo problemas jajajaja... y se ve tan facil las respuestas...U_U... -------------------- *Karen, la futura Diosa matemática...*
·:· |†| ..Poisoned Dreams.. |†| ·:· |
|
|
|
 Aug 10 2005, 05:46 PM Aug 10 2005, 05:46 PM
Publicado:
#8
|
|
|
Principiante Matemático Grupo: Usuario FMAT Mensajes: 2 Registrado: 10-August 05 Miembro Nº: 215 |
Encontre dificil la prueba por equipos de 1er nivel, pero habra que subir en la recuperativa no mas..
|
|
|
|
 Aug 10 2005, 07:39 PM Aug 10 2005, 07:39 PM
Publicado:
#9
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
CITA(Jonas Valdivieso @ Aug 10 2005, 06:46 PM) Encontre dificil la prueba por equipos de 1er nivel, pero habra que subir en la recuperativa no mas.. Efectivamente no fue tan sencilla...pero tampoco era imposible... Lo que pasa es que quizas no estaban acostumbrados a trabajar con cosas geometricas de ese estilo.. Bueno,y la intencion era que todos aprendieran a hacerlo...y creo que se logro el objetivo...ahora si les fue bien o mal..aun queda la recuperativa asi que hay que ponerle harto empeño pues es periodo de definiciones y todo puede cambiar con los resultados de esta ultima instancia... Te deseo la mejor de las suertes Saludos -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
 Aug 10 2005, 08:32 PM Aug 10 2005, 08:32 PM
Publicado:
#10
|
|
|
Matemático Grupo: Usuario FMAT Mensajes: 34 Registrado: 6-August 05 Desde: some place pwning noobs Miembro Nº: 167 |
CITA(SoLiD_UsHeR @ Aug 9 2005, 05:39 PM) mmmmm en esta parte de la fecha, la grupal tuvimos varios problemas...... Bueno .... es que nunca entendimos que las rectas las poniamos nosotros o tenia que estar buena en todos los ángulos en la recta.. aparte si nos salia en un solo caso, y por casualidad y luego lo probabamos con otro ángulo.... bueno eso.... bueno para eso estan los que tomamos pruebapo bueno y lo de angulos que mencionaste arriba, pues no era necesario trabaja con angulos -------------------- |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 11th April 2025 - 07:39 AM |





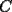 sobre la recta
sobre la recta 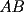 , distinto del punto
, distinto del punto 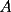 , tal que
, tal que 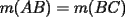
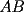 , que pasa por el punto
, que pasa por el punto 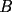
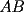
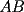
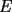 , sobre el trazo
, sobre el trazo 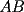 , tal que
, tal que 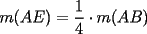 . Puede asumir que
. Puede asumir que 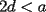
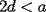
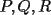 , encuentre la bisectriz del ángulo
, encuentre la bisectriz del ángulo 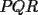
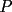 , fuera de la recta
, fuera de la recta 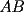 , y fuera de las rectas perpendiculares a la recta
, y fuera de las rectas perpendiculares a la recta 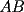 , pasando por
, pasando por 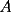 y por
y por 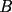 (o sea: las rectas
(o sea: las rectas 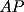 y
y 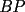 no son perpendiculares a la recta
no son perpendiculares a la recta 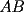 ), dibuje una recta paralela a la recta
), dibuje una recta paralela a la recta 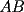 , que pase por el punto
, que pase por el punto 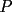
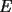 , sobre el trazo
, sobre el trazo 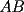 , tal que
, tal que 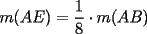
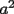
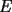 , sobre el trazo
, sobre el trazo 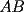 , tal que
, tal que