|
|
|
|
|
|
|
  |
 Aug 7 2005, 11:56 PM Aug 7 2005, 11:56 PM
Publicado:
#1
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
Y como lo prometido es deuda..partimos la nueva ronda de problemas...
Yo partire de inmediato con el problema 7,o sea el desafio de la semana Desafio de la Semana Sea ABC un triángulo y D el pie de la altura dese A. Consideramos dos puntos E y F, ambos distintos de D y pertenecientes a una misma recta por D, tales que AE es perpendicular a BE y AF es perpendicular a CF. Sean M y N los puntos medios de BC y EF, respectivamente. Demostrar que AN es perpendicular a NM. No es tan dificil...tampoco es facil..o sea es un muy buen problema para hacerlos pensar bastante..dado que se acerca la ultima fecha de la Interescolar y La Clasificacion de la Olimpiada Nacional Saludos -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
 Aug 8 2005, 10:06 PM Aug 8 2005, 10:06 PM
Publicado:
#2
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
Problema 1
Tenemos un conjunto de 221 números reales cuya suma es 110721. Los disponemos formando una tabla rectangular de modo que todas las filas y la primera y última columnas son progresiones aritméticas de más de un elemento. Probar que la suma de los elementos de las cuatro esquinas vale 2004 Suerte...y saludos -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
 Aug 8 2005, 10:43 PM Aug 8 2005, 10:43 PM
Publicado:
#3
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
Problema 2
Demostrar que si 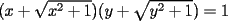 , entonces , entonces 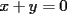 Suerte con este nuevo desafio..veamos si alguien nos da la solucion...y tambien veamos cual es la mas elegante...saludos -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
 Aug 8 2005, 11:20 PM Aug 8 2005, 11:20 PM
Publicado:
#4
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 293 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 3 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Aqui va la solucion para el problema 2)
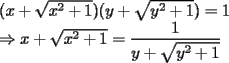 Racionalizando el lado derecho nos queda 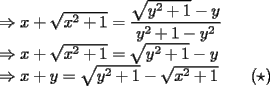 Análogamente, si comenzamos racionalizando el lado izquierdo (o bien, intercambiando los roles de  e e 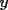 ): ):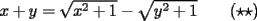 Sumando 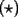 con con 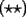 nos queda nos queda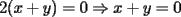 Saludos a todos --------------------  |
|
|
|
 Aug 10 2005, 11:09 AM Aug 10 2005, 11:09 AM
Publicado:
#5
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 558 Registrado: 14-May 05 Desde: Maipú, Stgo, Chile Miembro Nº: 27 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Problema 3:
Si a un triángulo le trazamos sus 3 transversales de gravedad, quedan 6 triángulos pequeños dentro del triángulo grande. Encuentre la relación entre las áreas de esos 6 triángulos. -------------------- El peor defecto del ignorante es que ignora su propia ignorancia................
|
|
|
|
| Corecrasher |
 Aug 10 2005, 01:10 PM Aug 10 2005, 01:10 PM
Publicado:
#6
|
|
Invitado |
CITA(Gp20 @ Aug 10 2005, 01:09 PM) Problema 3: Si a un triàngulo le trazamos sus 3 transversales de gravedad, quedan 6 triángulos pequeños dentro del triàngulo grande. Encuentre la relación entre las àreas de esos 6 triángulos.  Con el criterio posteado en este mensaje , en el que cuando hay 2 triangulos con la misma altura , se cumple las areas son a las bases ... , con esto podemos afirmar al cortar las transversales en puntos medios que hay 3 pares de areas iguales... , asu vez por lo mismo 2y+x=2z+x osea y=z luego mirando la relacion de las areas de los triangulos de base AD y DC podemos afirmar que 3z=2x+z osea x=z , concluimos que todas las areas son iguales |
|
|
|
 Aug 10 2005, 10:58 PM Aug 10 2005, 10:58 PM
Publicado:
#7
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
La solución a los problemas 2 y 3 están correctas. Ahora debemos publicar un nuevo problema (nos está pillando el tiempo)
Problema 4: Dado un 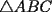 , y un punto , y un punto 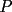 sobre su circunferencia circunscrita, llamaremos sobre su circunferencia circunscrita, llamaremos 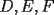 a las proyecciones ortogonales de a las proyecciones ortogonales de 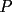 sobre los lados sobre los lados 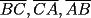 , respectivamente. Pruebe que los puntos , respectivamente. Pruebe que los puntos 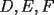 son colineales (esto abre una discusión sobre un "clásico" teorema geométrico) son colineales (esto abre una discusión sobre un "clásico" teorema geométrico)
-------------------- |
|
|
|
 Aug 10 2005, 11:36 PM Aug 10 2005, 11:36 PM
Publicado:
#8
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 293 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 3 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Mas vale tarde ke nunka
Problema 5 a)Determine para que enteros positivos  , , 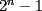 es divisible por 7 es divisible por 7b)Muestre que 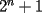 nunca es divisible por 7 nunca es divisible por 7c)Determine para que enteros positivos  , , 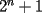 es divisible por 3 es divisible por 3Saludos a todos y suerte --------------------  |
|
|
|
 Aug 10 2005, 11:50 PM Aug 10 2005, 11:50 PM
Publicado:
#9
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Este problema me parece + entretenido que el 4 (que yo propuse hace un rato...). El nivel de ingenio lo hace de un nivel superior al CMAT, pero aún así la solución no deja de ser atractiva:
Problema 6: Sea 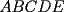 un pentágono convexo, tal que un pentágono convexo, tal que 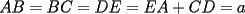 , y los ángulos en , y los ángulos en 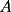 y y 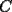 son rectos. Encuentre el área del pentágono en términos de son rectos. Encuentre el área del pentágono en términos de 
-------------------- |
|
|
|
 Aug 11 2005, 06:48 PM Aug 11 2005, 06:48 PM
Publicado:
#10
|
|
 Maestro Matemático Grupo: Usuario FMAT Mensajes: 116 Registrado: 14-May 05 Desde: Buin, Santiago Miembro Nº: 26 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
CITA(vverdugo @ Aug 11 2005, 01:36 AM) Mas vale tarde ke nunka Problema 5 a)Determine para que enteros positivos n, 2^n - 1 es divisible por 7 b)Muestre que 2^n + 1 nunca es divisible por 7 c)Determine para que enteros positivos n, 2^n + 1 es divisible por 3 Saludos a todos y suerte Ia..este problema es relativamente fácil..... a) Obviamente, para que se cumpla la condición del enunciado, se debe cumplir que 2^n = 1 (mod. 7). Pero, fijémonos las congruencias de las potencias de 2 e mod. 7 2^1 = 2 2^2 = 4 2^3 = 1 2^4 = 2 2^5= 4 2^6 = 1 ...... ...... ..... ..... Como ven se forma un ciclo 2,4,1 y por lo tanto para que 2^n = 1 (mod. 7), n = 3k, esto según el ciclo que se forma. b)Con lo mismo, no hay ninguna congruencia en el ciclo tal que 2^n = 6 (mod.7), asi que....no se puede ps... xD c)Ia...ahora hagamos lo mismo pero con las potencias de 2 en mod. 3 2^1 = -1 2^2 = 1 2^3 = -1 2^4 = 1 .... .... ... Y como ven se forma otro ciclo donde todas las potencia impares son congruentes con -1 y las pares con 1. Además, para que se cumpla que 2^n + 1 = 0 (mod. 3), entonces se debe cumplir que 2^n = -1 (mod. 3), y esto ocurre cuando n= 2k+1.... FIN!!! ....ven q era facilito?? ia...au revoir... QUEPD by MasTer® --------------------   "Lo que no entiendes hoy lo comprenderás mañana" |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 9th April 2025 - 02:51 AM |










