2 dudas pequeñitas - Foro fmat.cl

Reglamento Sector de Consultas

Para un correcto uso de este foro debes leer estas reglas:

Este Sector es donde pueden plantear sus dudas de Nivel Universitario.
- NO se debe usar el Banco de Problemas Resueltos para consultar.
Se solicita a los usuarios el uso de LaTeX, para que llevemos una conversación al nivel que este sector requiere
Hacer UNA CONSULTA por TEMA, ya que asi es mas facil enfocarse solo a la pregunta.
- Si desean hacer varias preguntas, tendran que crear un tema para cada una.
- con un limite de 5 de un mismo tema por usuario, pues lo mas probable es que se resuelvan de forma similar
Respecto al TITULO, tratar de ser lo mas claro posible de que trata la consulta.
- Ejemplo de lo que no se debe hacer: "ayuda porfis" ó "Heeeeeelp!"
NO hacer doble posteo de una misma duda
- Buscar antes de preguntar (se recomienda usar el Motor de Busqueda).
El usuario que realiza la consulta debe manifestar si la respuesta dada por la Comunidad le fue o no satisfactoria.
NO doble postear, demuestre compromiso con su consulta.
Use el botón "Editar" si olvido algún detalle.
Si necesita ayuda urgente, exprese lo que ha intentado para resolver el problema
Usuario que no cumpla estas reglas, sera advertido (en el mismo post o via MP).
- En caso que incurra nuevamente a faltar al reglamento, sera amonestado.

Staff FMAT

2 dudas pequeñitas, negación y conjuntos

alfacentauri Ver Perfil del Miembro Ver los mensajes de este miembro	Mar 20 2009, 05:41 PM Publicado: #1
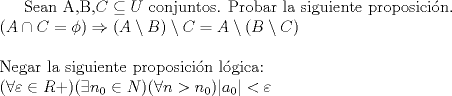
Maestro Matemático Grupo: Usuario FMAT Mensajes: 71 Registrado: 14-May 08 Desde: Santiago Miembro Nº: 23.151 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	hola...tengo problemas con 2 ejercicios $TEX: Sean A,B,$C\subseteq U$ conjuntos. Probar la siguiente proposición. \\<br />$(A\cap C = \phi) \Rightarrow (A\setminus B)\setminus C = A\setminus (B\setminus C)$ \\<br />\\<br />Negar la siguiente proposición lógica: \\<br />$(\forall \varepsilon \in R+)(\exists n_{0} \in N)(\forall n > n_{0})\|a_{0}\|< \varepsilon $$

Ussop Ver Perfil del Miembro Ver los mensajes de este miembro	Mar 20 2009, 05:50 PM Publicado: #2
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.349 Registrado: 8-October 07 Desde: Quilicura Miembro Nº: 11.057 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: \[<br />\begin{gathered}<br /> \left( {A \cap C = \emptyset } \right) \Rightarrow \left( {A - B} \right) - C = A - \left( {B - C} \right) \hfill \\<br /> \Rightarrow \left( {A \cap B^C } \right) \cap C^C = A \cap \left( {B \cap C^C } \right)^C \hfill \\<br /> \Rightarrow A \cap B^C \cap C^C = A \cap \left( {B^C \cup C} \right) \hfill \\<br /> \Rightarrow A \cap B^C = A \cap B^C \cup \emptyset \hfill \\<br /> \Rightarrow A \cap B^C = A \cap B^C \hfill \\ <br />\end{gathered} <br />\]<br />$ -------------------- Plan Comun Ingenieria USM 2009 Santiago Ingenieria Civil Electrica Usm 2010 Santiago

alfacentauri Ver Perfil del Miembro Ver los mensajes de este miembro	Mar 20 2009, 05:54 PM Publicado: #3
Maestro Matemático Grupo: Usuario FMAT Mensajes: 71 Registrado: 14-May 08 Desde: Santiago Miembro Nº: 23.151 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	¡¿¿HA???! ¿cómo eso que de la tercera a la cuarta linea desapareció el complemento de C?

Ussop Ver Perfil del Miembro Ver los mensajes de este miembro	Mar 20 2009, 05:57 PM Publicado: #4
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.349 Registrado: 8-October 07 Desde: Quilicura Miembro Nº: 11.057 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(alfacentauri @ Mar 20 2009, 06:54 PM) ¡¿¿HA???! ¿cómo eso que de la tercera a la cuarta linea desapareció el complemento de C? supuse pero no toy seguro, si la interseccion de A y C es un conjunto vacio A debe ser igual al complemento de C -------------------- Plan Comun Ingenieria USM 2009 Santiago Ingenieria Civil Electrica Usm 2010 Santiago

alfacentauri Ver Perfil del Miembro Ver los mensajes de este miembro	Mar 20 2009, 06:14 PM Publicado: #5
Maestro Matemático Grupo: Usuario FMAT Mensajes: 71 Registrado: 14-May 08 Desde: Santiago Miembro Nº: 23.151 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	y qué hay de la segunda?

kbzoon Ver Perfil del Miembro Ver los mensajes de este miembro	Mar 20 2009, 06:40 PM Publicado: #6
Dios Matemático Supremo Grupo: Colaborador Platinum Mensajes: 1.627 Registrado: 11-October 07 Desde: Suburbios de Conchalí Miembro Nº: 11.213 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Aquí les presento lo que hice: Si $TEX: \[<br />A \cap C = \emptyset \Rightarrow \left( {A\backslash B} \right)\backslash C = A\backslash \left( {B\backslash C} \right)<br />\]<br />$ podemos tomar cualquier lado de la igualdad para demostrar el resultado. En efecto: $TEX: \[<br />\left( {A\backslash B} \right)\backslash C = A \cap B^C \cap C^C \underbrace = _\underbrace {A \cap C^C }_A \cap B^C = A \cap B^C \underbrace = _{}\left( {A \cap B^C } \right) \cup \emptyset <br />\]<br />$ $TEX: \[<br /> = \left( {A \cap B^C } \right) \cup \left( {A \cap C} \right) = A \cap \left( {B^C \cup C} \right) = A \cap \left( {B\backslash C} \right)^C = A\backslash \left( {B\backslash C} \right)<br />\]<br />$ $TEX: \[<br />\blacksquare <br />\]<br />$ En $TEX: \[<br />\left( \right)<br />\]<br />$ se usó que $TEX: \[<br />A \cap C = \emptyset \Rightarrow A \subseteq C^C \vee C \subseteq A^C <br />\]<br />$ y en $TEX: \[<br />\left( {**} \right)<br />\]<br />$ se hace aparecer el neutro como $TEX: \[<br />A \cap C = \emptyset <br />\]<br />$ que viene de la hipótesis tb. Las propiedades usadas las pueden notar ustedes. Oye max, una cosa, cuando uno quiere probar una igualdad no puede asumir como cierta y atacar los dos lados paralelamente. Lo que se debe hacer es tomar un sólo lado de la igualdad y llegar al otro . Para la segunda recordar las negacioones del cuantificador existencial y el universal. Bye. -------------------- Injeniería de Minas. The best SpaceDream Radio ever

Ussop Ver Perfil del Miembro Ver los mensajes de este miembro	Mar 20 2009, 06:47 PM Publicado: #7
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.349 Registrado: 8-October 07 Desde: Quilicura Miembro Nº: 11.057 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(kbzoon @ Mar 20 2009, 07:40 PM) Aquí les presento lo que hice: Si $TEX: \[<br />A \cap C = \emptyset \Rightarrow \left( {A\backslash B} \right)\backslash C = A\backslash \left( {B\backslash C} \right)<br />\]<br />$ podemos tomar cualquier lado de la igualdad para demostrar el resultado. En efecto: $TEX: \[<br />\left( {A\backslash B} \right)\backslash C = A \cap B^C \cap C^C \underbrace = _\underbrace {A \cap C^C }_A \cap B^C = A \cap B^C \underbrace = _{}\left( {A \cap B^C } \right) \cup \emptyset <br />\]<br />$ $TEX: \[<br /> = \left( {A \cap B^C } \right) \cup \left( {A \cap C} \right) = A \cap \left( {B^C \cup C} \right) = A \cap \left( {B\backslash C} \right)^C = A\backslash \left( {B\backslash C} \right)<br />\]<br />$ $TEX: \[<br />\blacksquare <br />\]<br />$ En $TEX: \[<br />\left( \right)<br />\]<br />$ se usó que $TEX: \[<br />A \cap C = \emptyset \Rightarrow A \subseteq C^C \vee C \subseteq A^C <br />\]<br />$ y en $TEX: \[<br />\left( {**} \right)<br />\]<br />$ se hace aparecer el neutro como $TEX: \[<br />A \cap C = \emptyset <br />\]<br />$ que viene de la hipótesis tb. Las propiedades usadas las pueden notar ustedes. Oye max, una cosa, cuando uno quiere probar una igualdad no puede asumir como cierta y atacar los dos lados paralelamente. Lo que se debe hacer es tomar un sólo lado de la igualdad y llegar al otro . Para la segunda recordar las negacioones del cuantificador existencial y el universal. Bye. ok que bueno que me lo dijiste ahora y no un profesor despues de una prueba -------------------- Plan Comun Ingenieria USM 2009 Santiago Ingenieria Civil Electrica Usm 2010 Santiago

Ussop Ver Perfil del Miembro Ver los mensajes de este miembro	Mar 20 2009, 07:04 PM Publicado: #8
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.349 Registrado: 8-October 07 Desde: Quilicura Miembro Nº: 11.057 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: \[<br />\begin{gathered}<br /> p = \left( {\forall \varepsilon \in \mathbb{R} + } \right)\left( {\exists n_0 \in \mathbb{N}} \right)\left( {\forall n \succ n_0 } \right)\left\| {a_0 } \right\| \prec \varepsilon \hfill \\<br /> \neg p = \left( {\exists \varepsilon \in \mathbb{R} + } \right)\left( {\forall n_0 \in \mathbb{N}} \right)\left( {\exists n \leqslant n_0 } \right)\left\| {a_0 } \right\| \geqslant \varepsilon \hfill \\ <br />\end{gathered} <br />\]$ Mensaje modificado por Ussop el Mar 20 2009, 07:23 PM -------------------- Plan Comun Ingenieria USM 2009 Santiago Ingenieria Civil Electrica Usm 2010 Santiago

alfacentauri Ver Perfil del Miembro Ver los mensajes de este miembro	Mar 20 2009, 07:07 PM Publicado: #9
Maestro Matemático Grupo: Usuario FMAT Mensajes: 71 Registrado: 14-May 08 Desde: Santiago Miembro Nº: 23.151 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Una cosa sí...no entiendo muy bien este paso $TEX: \[<br /> \left( {A \cap B^C } \right) \cup \left( {A \cap C} \right) = A \cap \left( {B^C \cup C} \right)<br />\]<br /><br />$ porque si aplicara distributividad no quedaría 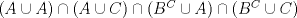$TEX: $(A\cup A)\cap (A \cup C)\cap (B^C \cup A)\cap (B^C \cup C)$$ ?

Ussop Ver Perfil del Miembro Ver los mensajes de este miembro	Mar 20 2009, 07:14 PM Publicado: #10
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.349 Registrado: 8-October 07 Desde: Quilicura Miembro Nº: 11.057 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(alfacentauri @ Mar 20 2009, 08:07 PM) Una cosa sí...no entiendo muy bien este paso $TEX: \[<br /> \left( {A \cap B^C } \right) \cup \left( {A \cap C} \right) = A \cap \left( {B^C \cup C} \right)<br />\]<br /><br />$ porque si aplicara distributividad no quedaría 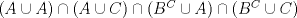$TEX: $(A\cup A)\cap (A \cup C)\cap (B^C \cup A)\cap (B^C \cup C)$$ ? Es que no aplico distribuidad, hizo que algo que estaba distribuido volviera a como era antes -------------------- Plan Comun Ingenieria USM 2009 Santiago Ingenieria Civil Electrica Usm 2010 Santiago

« Posterior · Consultas de la Semana · Anterior »

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):