|
|
|
|
|
|
|
  |
 Mar 14 2009, 11:10 PM Mar 14 2009, 11:10 PM
Publicado:
#1
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.189 Registrado: 17-September 08 Desde: chernobyl Miembro Nº: 34.593 Nacionalidad:  Universidad:  Sexo:  |
![TEX: \[<br />\begin{gathered}<br /> 1.\left( {p - 1} \right)! \equiv - 1\left( {\bmod p} \right) \hfill \\<br /> 2.\left( {a + b} \right)^p \equiv a^p + b^p \left( {\bmod p} \right) \hfill \\ <br />\end{gathered} <br />\]](./tex/fac4c6ab9471187667f1516b44a6baca.png) ojala me puedan ayudar, de antemano muchas gracias -------------------- Estudiante II año de Ingenieria Civil en Obras Civiles - UACh
|
|
|
|
 Mar 14 2009, 11:16 PM Mar 14 2009, 11:16 PM
Publicado:
#2
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.139 Registrado: 11-June 08 Desde: UK Miembro Nº: 26.837 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
ambos problemas estan demostrados en el sector de olimpiadas
saludos -------------------- blep
|
|
|
|
 Mar 15 2009, 01:18 AM Mar 15 2009, 01:18 AM
Publicado:
#3
|
|
 Dios Matemático Grupo: Team Ensayos FMAT Mensajes: 309 Registrado: 2-December 08 Desde: Cerro Navia Miembro Nº: 40.183 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Sugerencia:
El ejercicio tiene que decir que 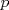 es primo. es primo. |
|
|
|
 Mar 18 2010, 12:53 AM Mar 18 2010, 12:53 AM
Publicado:
#4
|
|
|
Dios Matemático Supremo Grupo: Super Moderador Mensajes: 2.065 Registrado: 25-May 08 Desde: Pelotillehue Miembro Nº: 24.463 |
El primero es conocido bajo el nombre de teorema de Wilson. Ya ha sido discutido por acá. Para el segundo usa el teorema del binomio y el hecho de p divide a
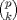 para cada natural k en [1,p-1]. para cada natural k en [1,p-1].
-------------------- "Please forget everything you have learned in school; for you haven't learned it... Please keep in mind at all times the corresponding portions of your school curriculum; for you haven't actually forgotten them." -- E. Landau
|
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 4th April 2025 - 05:02 AM |






![TEX: \[<br />\begin{gathered}<br /> \underline {{\text{Algunas Constantes}}} {\text{:}} \hfill \\<br /> \bullet {\text{ Constante de Catalan : }}G = \sum\limits_{K = 1}^\infty {\frac{{\left( { - 1} \right)^k }}<br />{{\left( {2k + 1} \right)^2 }}} {\text{ }}\left( {{\text{no demostrado}}} \right) \hfill \\<br /> \bullet {\text{ Constante de Liouville: }}\sum\limits_{k = 0}^\infty {10^{ - k} } = 0,1100010000000000.. \hfill \\<br /> \bullet {\text{ Constante de Hilbert: }}\sqrt 2 ^{\sqrt 2 } \hfill \\<br /> \bullet {\text{ Constante de Euler}} - {\text{Mascheroni: }}\gamma = 0,577215...({\text{no demostrado)}} \hfill \\<br /> \bullet {\text{ Constante de Morse}} - {\text{Thue: 0}}{\text{,01101001}}... \hfill \\<br /> \bullet {\text{ }}i^i = 0,207879576..... \hfill \\<br /> \bullet {\text{ Constante de Copeland}} - {\text{Erdos: 0}}{\text{,23571113171923}}... \hfill \\<br /> \bullet {\text{ }}\pi = 3,14159265... \hfill \\<br /> \bullet {\text{ }}e = 2,71828183.... \hfill \\ <br />\end{gathered} <br />\]](./tex/a801ee37e623c659a089977115a29b16.png)




