|
|
|
|
|
|
|
  |
 Mar 6 2009, 06:07 PM Mar 6 2009, 06:07 PM
Publicado:
#1
|
|
|
Principiante Matemático Destacado Grupo: Usuario FMAT Mensajes: 15 Registrado: 12-February 08 Miembro Nº: 15.484 Nacionalidad:  Sexo:  |
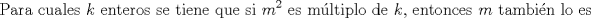 Gracias! |
|
|
|
 Mar 6 2009, 06:46 PM Mar 6 2009, 06:46 PM
Publicado:
#2
|
|
|
Principiante Matemático Destacado Grupo: Usuario FMAT Mensajes: 15 Registrado: 12-February 08 Miembro Nº: 15.484 Nacionalidad:  Sexo:  |
AYUDAAAAAAAAAAAAAAAAAAAAAAAA
ALGUIEN!!! |
|
|
|
 Mar 6 2009, 07:17 PM Mar 6 2009, 07:17 PM
Publicado:
#3
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.812 Registrado: 4-November 07 Desde: Santiago Miembro Nº: 12.213 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Como
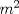 es múltiplo de es múltiplo de 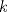 entonces se cumple que entonces se cumple que  para algún para algún  . Luego, si . Luego, si  también es múltiplo de también es múltiplo de 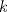 se deberá cumplir que se deberá cumplir que 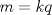 para algún para algún 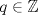 y por lo anterior, y por lo anterior, 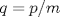 . .Es decir, la premisa es verdadera para todo 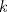 que al multiplicarlo por algún entero divisible por que al multiplicarlo por algún entero divisible por  resulte resulte 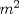 . .No sé si era lo que esperabas (o si se podrá profundizar más) PD: 45 mins, un viernes, semana novata... no será mucho? -------------------- |
|
|
|
 Mar 6 2009, 07:31 PM Mar 6 2009, 07:31 PM
Publicado:
#4
|
|
|
Principiante Matemático Destacado Grupo: Usuario FMAT Mensajes: 15 Registrado: 12-February 08 Miembro Nº: 15.484 Nacionalidad:  Sexo:  |
Es que en realidad a lo que yo llegué es que k puede ser alguna combinación (cualquiera) de los factores primos de m.
Pero, necesito como demostrarlo de manera "formal", porque llegué a eso haciendo mil ejemplos jaajja |
|
|
|
 Mar 6 2009, 07:42 PM Mar 6 2009, 07:42 PM
Publicado:
#5
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.812 Registrado: 4-November 07 Desde: Santiago Miembro Nº: 12.213 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Si, pero en gral para cualquier m q sea multiplo de k, k debe ser alguna combinacion de los factores primos de m y los que le faltan a la combinacion se los entrega q, así q no sé q tanto te sirva eso. De dónde es este ejercicio?
-------------------- |
|
|
|
 Mar 6 2009, 11:37 PM Mar 6 2009, 11:37 PM
Publicado:
#6
|
|
|
Principiante Matemático Destacado Grupo: Usuario FMAT Mensajes: 15 Registrado: 12-February 08 Miembro Nº: 15.484 Nacionalidad:  Sexo:  |
Si, pero en gral para cualquier m q sea multiplo de k, k debe ser alguna combinacion de los factores primos de m y los que le faltan a la combinacion se los entrega q, así q no sé q tanto te sirva eso. De dónde es este ejercicio? Sí po, cierto. Pero lo que digo es que "los enteros k" que cumplen la condición requerida, son necesariamente los k que se obtienen como alguna combinación de los múltiplos primos de m, y por lo tanto No existe un k, que no sea combinación de multiplos primos de m, que cumpla. Entonces, me parece que definiendo a k como combinación de multiplos primos de m, es razón suficiente para responder la pregunta. O dicho de otra forma: "TODOS los entero k que cumplen la condición requerida, son necesariamente factores primos de m, y no hay otros." Además, tomando en cuenta lo que me dijiste, si yo escribo 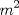 como  , luego puedo escribir cada m como una multiplicación de sus factores primos, y por lo tanto k TIENE que ser alguna combinación de esos múltiplos primos, ya que , luego puedo escribir cada m como una multiplicación de sus factores primos, y por lo tanto k TIENE que ser alguna combinación de esos múltiplos primos, ya que 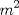 es múltiplo de k. No queda otra. es múltiplo de k. No queda otra.Ahora, el problema es que no me parece una respuesta muy convincente jaja. y tampoco llegué a esa conclusión "genéricamente" sino que probando con muchos casos, por eso necesito una demostración que en realidad avale lo que obtuve empíricamente. aaah, y el ejercicip es de cálculo 1 en la PUC Mensaje modificado por bellet el Mar 6 2009, 11:39 PM |
|
|
|
 Mar 7 2009, 12:58 AM Mar 7 2009, 12:58 AM
Publicado:
#7
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.812 Registrado: 4-November 07 Desde: Santiago Miembro Nº: 12.213 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Sí po, cierto. Pero lo que digo es que "los enteros k" que cumplen la condición requerida, son necesariamente los k que se obtienen como alguna combinación de los múltiplos primos de m, y por lo tanto No existe un k, que no sea combinación de multiplos primos de m, que cumpla. Entonces, me parece que definiendo a k como combinación de multiplos primos de m, es razón suficiente para responder la pregunta. O dicho de otra forma: "TODOS los entero k que cumplen la condición requerida, son necesariamente factores primos de m, y no hay otros." Además, tomando en cuenta lo que me dijiste, si yo escribo 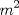 como  , luego puedo escribir cada m como una multiplicación de sus factores primos, y por lo tanto k TIENE que ser alguna combinación de esos múltiplos primos, ya que , luego puedo escribir cada m como una multiplicación de sus factores primos, y por lo tanto k TIENE que ser alguna combinación de esos múltiplos primos, ya que 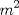 es múltiplo de k. No queda otra. es múltiplo de k. No queda otra.Ahora, el problema es que no me parece una respuesta muy convincente jaja. y tampoco llegué a esa conclusión "genéricamente" sino que probando con muchos casos, por eso necesito una demostración que en realidad avale lo que obtuve empíricamente. aaah, y el ejercicip es de cálculo 1 en la PUC Me refería a que la respuesta tenía un alto grado de trivialidad, es decir, andaba cerca de responder: k debe ser un entero. Yo no me manejo mucho más allá con el temita de los primos, números, etc. En too caso, este tipo de preguntas no es muy popular asi q no te preocupi mucho, dudo que te vaya a salir en una prueba. -------------------- |
|
|
|
 Mar 7 2009, 08:19 AM Mar 7 2009, 08:19 AM
Publicado:
#8
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.139 Registrado: 11-June 08 Desde: UK Miembro Nº: 26.837 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
 saludos Mensaje modificado por snw el Mar 7 2009, 08:20 AM -------------------- blep
|
|
|
|
 Mar 7 2009, 09:35 AM Mar 7 2009, 09:35 AM
Publicado:
#9
|
|
|
Principiante Matemático Destacado Grupo: Usuario FMAT Mensajes: 15 Registrado: 12-February 08 Miembro Nº: 15.484 Nacionalidad:  Sexo:  |
Ya, con las respuestas que me dieron ambos me parece suficiente para cerrar el ejercicio y "move on". No creo que haya más vuelta que darle en verdad jajaja.
Gracias!!! me sirvió harto! Mensaje modificado por bellet el Mar 7 2009, 10:23 AM |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 3rd April 2025 - 04:56 PM |











![TEX: \[\mathfrak{L}=\int_{-\infty}^\infty e^{-289x^2}dx=\frac{\Gamma (\frac{1}{2})}{17}=\frac{\sqrt{\pi}}{17}\]](./tex/e0e88dba678ca3ead120b088f41191b2.png)


