|
|
|
|
|
|
|
  |
 May 13 2005, 03:16 AM May 13 2005, 03:16 AM
Publicado:
#1
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
Bueno..pensando desde ya en la Olimpiada Nacional les posteo los problemas de la Clasificacion y de la Final Nacional del Nivel Mayor de la Olimpiada Nacional de Matematicas..asi que posteen sus soluciones...(aqui hasta los entrenadores se podrian pegar su ayudadita posteando los que ellos hicieron
![TEX: \noindent \underline{$Clasificacion\ Nacional$}\\<br />\\<br />\textbf{P1)} Investigue si existe un numero entero positivo $N$ tal que si se borra el primer digito de su expresion decimal, resulta un numero $p$ tal que $N$ es 58 veces $p$.\\<br />\\<br />\textbf{P2)} Influenciados por los triunfos de Gonzalez y Massu, en un curso de un colegio mixto decidieron organizar un torneo de tenis. Participaron $n$ ni\~nas y $2n$ ni\~nos.Cada par de participantes de los $3n$ estudiantes, se enfrento en exactamente un partido. Despues del torneo se calculo la razon entre el numero de victorias de las ni\~nas y el numero de victorias de los ni\~nos, \mbox{resultando} ser esta razon igual a 7:5. Determine $n$ y demuestre que en todo partido en que se enfrento una ni\~na con un ni\~no, la ni\~na resulto vencedora.\\<br />\\<br />\textbf{P3)} En cierto pais existe una comunicacion ferroviaria directa entre cualquier par de ciudades, pero los trenes viajan solamente en una direccion. Pruebe que existe una de dichas ciudades, desde la cual se puede llegar a cualquier otra ciudad pasando a lo mas por una intermedia.\\<br />\\<br />\textbf{P4)} Encuentre al menos un cuarteto de numeros enteros positivos $m$, $n$, $p$, $q$ disntintos entre si, que satisfagan las relaciones:\\<br />\\<br />$m+n=p+q$\\<br />$\sqrt{m}+\sqrt[3]{n}=\sqrt{p}+\sqrt[3]{q}>2004$\\<br />\\<br />\textbf{P5)} Sea $ABCD$ un cuadrilatero convexo tal que cada uno de sus lados es menos que 20. Prueba que para cualquier punto $P$ interior al cuadrilatero, al menos una de las distancias $PA$, $PB$, $PC$, $PD$ es menor que 15. ?` Puede afirmarse que al menos una de dichas distancias es menor que 14 ?\\<br />\\<br />\textbf{P6)} En el pizarron un profesor escribio varios ceros,unos y dos. Luego con estos numeros se hizo la siguiente operacion: se borro dos numeros \mbox{distintos} entre si y en vez de ellos en el pizarron se escribio un numero diferente a los borrados(por ejemplo, si se borra un 1 y un 2,despues se escribe un 0). Tras hacer varias veces esta operacion, en el pizarron quedo escrito un solo \mbox{numero}. Investigue si este numero depende del orden en el que se fue realizando las borraduras.](./tex/61113.gif)  Bueno...estoy algo cansado..espero mas ratito animarme a postear los problemas de la fase Final del Nivel Mayor... Saludos PD:Espero que posteen sus soluciones asi como espero que los entrenadores nos delumbren con las soluciones que ellos entregaron cuando dieron la prueba...(me consta que en ocasiones eran mas novedosas que las soluciones del jurado de la Olimpiada -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
 May 16 2005, 02:24 AM May 16 2005, 02:24 AM
Publicado:
#2
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
Bueno..y como lo prometido es deuda..aqui van los problemas de la Final Nacional
P1 ) Una empresa con 2004 trabajadores,celebro su aniversario invitando a todos a un almuerzo servido en una mesa redonda.Cuando se sentaron alrededor de esta mesa los 2004 trabajadores, formaron un circulo de personas y al poco tiempo descubrieron que todos ellos tenian salario distinto y ademas que la diferencia entre los sueldos de dos vecinos cualesquiera,en la mesa redonda,era de 2000 o bien 3000 pesos.Calcule la maxima diferencia que puede haber entre los sueldos de estos trabajadores. P2 ) Todo punto de una recta esta pintado de color rojo o bien de color azul.Demuestre que siempre existen tres puntos A,B,C que estan pintados de igual color y son tales que el punto B es el punto medio del segmento AC. P3 ) El perimetro,es decir, la suma de las longitudes de todos los lados de un cuadrilatero convexo ABCD, es igual a 2004 metros; mientras que la longitud de su diagonal AC es igual a 1001 metros. Investigue si la longitud de la otra diagonal BD puede: i)Ser igual a solo un metro ii)ser igual a la longitud de la diagonal AC P4 ) Se toma el numero 2^2004 y se calcula la suma S de todos sus digitos.Luego se calcula la suma de todos los digitos de S para obtener R.A continuacion se calcula la suma de todos los digitos de R y asi sucesivamentehasta llegar a un numero de un solo digito.Encuentrelo.(Por ejemplo si tomamos 2^7-128,encontramos que S=11,R=2.Asi en este caso de 2^7 el digito buscado sera 2) P5 ) Sobre la superficie infinita del mar flota una mancha de petroleo negra y acotada.Al cabo de cada minuto la mancha y el mar cambian segun la sigueinte ley:en cada punto P del mar(o de la mancha) se considera un disco D de radio 1 centrado en P.Si mas de la mitad del area dentro del disco D tiene color negro,el punto P permanecera negro durante el proximo minuto.Si mas de la mitad del area dentro del disco D esta de color azul marino,el punto P tendra color azul marino durante el minuto siguiente.En el caso de que tanto el area limpia como la contaminada dentro del disco D sean iguales,su centro P no cambiara de color.¿Puede aquella mancha "vivir" siempre o desaparecera en algun momento? P6 ) Los segmentos AB,BC y CD de la poligonal ABCD tienen la misma longitud y son tangentes a una circunferencia S,de centro el punto O.Sea P el punto de tangencia de BC con S, y sea Q el punto de interseccion de las rectas AC y BD.Demuestre que el punto Q es colineal con los puntos P y O. |
|
|
|
 May 29 2005, 05:36 PM May 29 2005, 05:36 PM
Publicado:
#3
|
|
 Matemático Grupo: Usuario FMAT Mensajes: 32 Registrado: 26-May 05 Desde: Santiago Miembro Nº: 59 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Ya pues chiquillos, animense a tratar de resolver los problemas, ya llevan algún tiempo ahí, y todavía ningún post tratando de solucionar alguno, bueno, ánimo y sigan intentando
-------------------- Orly
|
|
|
|
 Jun 10 2005, 12:47 AM Jun 10 2005, 12:47 AM
Publicado:
#4
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 293 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 3 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Solucion problema 6 final: (aprendiendo a ocupar cabri
 screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img112.imageshack.us/img112/7417/fmat113qu.png');}" /> screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img112.imageshack.us/img112/7417/fmat113qu.png');}" />Trazemos los segmentos OB y OC. Tenemos que <ABO=<OBC=x, puesto que los triangulos BTO y BPO son congruentes (<OTB=<OPB=90, entonces BT^2=OB^2 - OT^2 y BP^2=OB^2 - OP^2, pero OT=OP, por que son radios de S, entonces BT^2=BP^2 => BT=BP, y por lo tanto BTO y BPO son congruentes por LLL ), y analogamente <PCO=<RCO=y. Como los triangulos ABC y BCD son isosceles, entonces la bisectriz que va del angulo "verticial" tambien es altura, y por lo tanto OB perp AC y OC perp BD. Ahora notemos en el triangulo BOC ya hay dos alturas trazadas. y por lo tanto el segmento que va de O a BC pasando por Q tambien lo es, y por lo tanto OP' perp BC. Pero OP tambien es perp a BC (P es el punto de tangencia), y por lo tanto P y P' coinciden. Luego, O, Q y P son colineales. Nos vemos :hola: --------------------  |
|
|
|
 Jun 11 2005, 05:32 PM Jun 11 2005, 05:32 PM
Publicado:
#5
|
|
 Maestro Matemático Grupo: Usuario FMAT Mensajes: 116 Registrado: 14-May 05 Desde: Buin, Santiago Miembro Nº: 26 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Hola...taba bn desaperecido...pero...bueno....vamos a hacer algo...almenos la parte uno del problema 3 x ahora...la dos.,.no alcanzo a hacerla ahora....asi q después la posteo...
P3 ) El perimetro,es decir, la suma de las longitudes de todos los lados de un cuadrilatero convexo ABCD, es igual a 2004 metros; mientras que la longitud de su diagonal AC es igual a 1001 metros. Investigue si la longitud de la otra diagonal BD puede: i)Ser igual a solo un metro ii)ser igual a la longitud de la diagonal AC SOL i) Veamos la siguiente figura...  Como se ve en la figura, BD = BE + DE y AE + CE = 1001 Ahora bien, aplicaremos algunas desigualdades de triángulos... ¤ BE + AE > AB ¤ BE + CE > BC ¤ DE + CE > CD ¤ DE + AE > AD -------------------------------- SUMANDO 2(DE + BE) + 2 (AE + CE) > 2004 ( AB+BC+CD+AD=PERÍMETRO=2004) 2(DE + BE) + 2*1001 > 2004 2(DE + BE) + 2002 > 2004 / - 2002 2(DE + BE) > 2 / *1/2 DE + BE >1 -------------------- | BD >1 | --------------------- Por lo tanto no puede ser 1 ....gracias... De la dos...solo llevo esto CD + CB > BC AB + AD > BC ------------------ SUMANDO AB + CB + CD + AD > 2*BC 2004 > 2*BC 1002 > BC Pero creo que algo le falta a eso...no sé...no se ve muy bien lo último....bueno..eso...nos estamos viendo....Adiós by mAstEr® --------------------   "Lo que no entiendes hoy lo comprenderás mañana" |
|
|
|
 Aug 4 2005, 07:03 PM Aug 4 2005, 07:03 PM
Publicado:
#6
|
|
 Maestro Matemático Grupo: Usuario FMAT Mensajes: 116 Registrado: 14-May 05 Desde: Buin, Santiago Miembro Nº: 26 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
P1 Clasificación: Investigue si existe un numero entero positivo N tal que si se borra el primer digito de su expresion decimal,resulta un numero p tal que N es 58 veces p.
R= Sea N=a*10^k + p (donde k es un número entero positivo). Supongamos que el enunciado es verdadero, es decir que N=58p, tenemos que: 58p=a*10^k+p, entonces 57p=a*10^k La primera conclusión que podemos sacar es que p=10k (aunque esto no nos servirá en el resultado final Entonces, veamos que congruencia nos combiene utilizar. Fijémonos que 57=3*19, entonces, podemos usar congruencia en mod. 3 ó 9. Obsevermos que: 10 ≡ -9 (mod. 19) ==> 10^k ≡ (-9)^k (mod. 19) y que 10 ≡ 1 (mod. 3) ==> 10^k ≡ 1^k (mod. 3) ==> 10^k ≡ 1 (mod.3) Luego: 57p ≡ a*10^k (mod. 3) 3*19p ≡ a*1 (mod.3) 0 ≡ a (mod. 3) Entonces, a puede tomar los valores de 3,6 ó 9 (ya que a es un dígito distinto de 0) 57p ≡ a*10^k (mod.19) 3p*19 ≡ a*10^k (mod. 19) 0 ≡ a*(-9)^k (mod. 19) Luego a=19b , pero como a es un dígito, que puede ser 3,6 ó 9, tenemos una contradicción. Entonces, no existe N con las condiciones pedidas. by mAsTeR® --------------------   "Lo que no entiendes hoy lo comprenderás mañana" |
|
|
|
 Aug 4 2005, 07:46 PM Aug 4 2005, 07:46 PM
Publicado:
#7
|
|
 Maestro Matemático Grupo: Usuario FMAT Mensajes: 116 Registrado: 14-May 05 Desde: Buin, Santiago Miembro Nº: 26 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
P4 ) Se toma el numero 2^2004 y se calcula la suma S de todos sus digitos.Luego se calcula la suma de todos los digitos de S para obtener R.A continuacion se calcula la suma de todos los digitos de R y asi sucesivamentehasta llegar a un numero de un solo digito.Encuentrelo.(Por ejemplo si tomamos 2^7-128,encontramos que S=11,R=2.Asi en este caso de 2^7 el digito buscado sera 2)
Veamos los siguientes resultados siguiente del número buscado en cada caso: 2^0=1 ==> 1 2^1=2 ==> 2 2^2=4 ==> 4 2^3=8 ==> 8 2^4=16 ==>7 2^5=32 ==>5 2^6=64 =>10 ==> 1 2^7=128 =>11 ==> 2 2^8=256 =>13==> 4 2^9=512 ==>8 2^10= 1024 ==>7 2^11= 2048 =>14 ==> 5 2^12 = 4096=>19 =>10 ==> 1 ..... .... .... Y así se ve como se va formando un ciclo [1,2,4,8,7,5] Por lo tanto para calcular S de 2^2004 se deber ver el lugar de 2^2004 en el ciclo. Como el ciclo parte en 0, entonces se encuentra en la posición 2^2004 se encuentra en la posición 2005 del ciclo. Ahora 2005 deja resto 1 en la división por 6 (el total de elementos del ciclo), entonces, El número buscado es 1. by mAsTeR® --------------------   "Lo que no entiendes hoy lo comprenderás mañana" |
|
|
|
 Aug 4 2005, 08:54 PM Aug 4 2005, 08:54 PM
Publicado:
#8
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Viendo las soluciones que pusiste, comento brevemente una de ellas
El problema donde planteaste 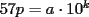 , fíjate que el lado derecho es múltiplo de 19, pero no es posible ver que , fíjate que el lado derecho es múltiplo de 19, pero no es posible ver que 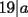 o bien que o bien que 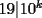 . El problema es rápido de resolver . El problema es rápido de resolver
-------------------- |
|
|
|
 Dec 31 2010, 10:10 AM Dec 31 2010, 10:10 AM
Publicado:
#9
|
|
 Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 193 Registrado: 22-March 07 Desde: San Miguel, Santiago Miembro Nº: 4.651 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Clasificación Problema 1
Sea 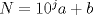 donde donde  es un dígito y es un dígito y 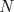 tiene tiene 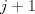 dígitos. Por enunciado dígitos. Por enunciado 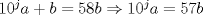 y como y como 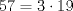 y y 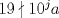 tal tal 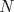 no existe. no existe.
-------------------- |
|
|
|
 Dec 31 2010, 10:52 AM Dec 31 2010, 10:52 AM
Publicado:
#10
|
|
 Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 193 Registrado: 22-March 07 Desde: San Miguel, Santiago Miembro Nº: 4.651 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Final Problema 4
Recordemos que todo numero es congruente a la suma de sus cifras en mod.9 (Propuesto para el lector, como indicación utilizar descomposición decimal y mod.9). Usando lo anterior sucesivamente tenemos que el numero final es congruente al inicial en mod.9, notemos que 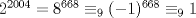 , así el numero final necesariamente es , así el numero final necesariamente es 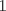 . .
-------------------- |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 26th April 2025 - 05:46 AM |








