|
|
|
|
|
|
|
  |
 Feb 19 2009, 10:28 PM Feb 19 2009, 10:28 PM
Publicado:
#1
|
|
 Dios Matemático Grupo: Team Ensayos FMAT Mensajes: 309 Registrado: 2-December 08 Desde: Cerro Navia Miembro Nº: 40.183 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Hallar la probabilidad de que una cuerda trazada al azar sobre una circunferencia sea mayor que el radio.
(Fundamente su respuesta). Saludos Mensaje modificado por psepulveda el Feb 19 2009, 10:33 PM |
|
|
|
 Feb 19 2009, 11:10 PM Feb 19 2009, 11:10 PM
Publicado:
#2
|
|
|
Dios Matemático Supremo Grupo: Baneado Mensajes: 1.737 Registrado: 6-September 07 Miembro Nº: 9.900 |
Mensaje modificado por deixo el Feb 19 2009, 11:46 PM |
|
|
|
 Feb 19 2009, 11:20 PM Feb 19 2009, 11:20 PM
Publicado:
#3
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 920 Registrado: 14-October 08 Miembro Nº: 36.137 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
[attachment=21389:Dibujo.PNG]
![TEX: \[<br />\begin{gathered}<br /> {\text{la probabilidad es igual al couciente entre el perimetro circular}} \hfill \\<br /> {\text{del pedazo celeste y perimetro total de la circunferencia}} \hfill \\<br /> \frac{2}<br />{3} \hfill \\ <br />\end{gathered} <br />\]](./tex/4e263cd03c36cd4887bd8d802eacb72f.png)
Mensaje modificado por pablomarcelo el Feb 19 2009, 11:21 PM |
|
|
|
 Feb 19 2009, 11:24 PM Feb 19 2009, 11:24 PM
Publicado:
#4
|
|
 Dios Matemático Grupo: Team Ensayos FMAT Mensajes: 309 Registrado: 2-December 08 Desde: Cerro Navia Miembro Nº: 40.183 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
|
|
|
|
 Feb 19 2009, 11:29 PM Feb 19 2009, 11:29 PM
Publicado:
#5
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 920 Registrado: 14-October 08 Miembro Nº: 36.137 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
|
|
|
|
 Feb 19 2009, 11:36 PM Feb 19 2009, 11:36 PM
Publicado:
#6
|
|
 Dios Matemático Grupo: Team Ensayos FMAT Mensajes: 309 Registrado: 2-December 08 Desde: Cerro Navia Miembro Nº: 40.183 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
No sé si estoy pensando igual que tú, pero creo que estás dejando de lado muchos casos favorables. |
|
|
|
 Feb 19 2009, 11:41 PM Feb 19 2009, 11:41 PM
Publicado:
#7
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.767 Registrado: 21-January 08 Desde: Santiago - Ancud Miembro Nº: 14.865 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Qué hay de la respuesta que te envié por mp psepulveda? no he puesto el desarrollo porque es un poco largo x)
-------------------- Estudia para superarte a ti mismo, no al resto. |
|
|
|
 Feb 20 2009, 12:26 AM Feb 20 2009, 12:26 AM
Publicado:
#8
|
|
|
Dios Matemático Supremo Grupo: Baneado Mensajes: 1.737 Registrado: 6-September 07 Miembro Nº: 9.900 |
Yo creo que los casos favorables están dentro de la circunferencia inscrita en el hexágono. por eso te faltaron unos trazos por destacar... Saludos! |
|
|
|
 Feb 20 2009, 02:06 PM Feb 20 2009, 02:06 PM
Publicado:
#9
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.767 Registrado: 21-January 08 Desde: Santiago - Ancud Miembro Nº: 14.865 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
La probabilidad de que una cuerda trazada al azar sobre una circunferencia sea mayor que el radio, estará dada por el cociente área sobreada/área total:
 asdf.png ( 47.03k )
Número de descargas: 6
asdf.png ( 47.03k )
Número de descargas: 6donde el área está limitada por dos cuerdas mínimas paralelas de largo r (es decir, estaríamos encerrando toda el área del círculo en la que si se traza una cuerda, esta medirá a lo menos r). La posición de los trazos respecto a la circunferencia es genérica, por lo que si se traza una cuerda no paralela a las trazadas en el dibujo, bastaría rotar los trazos para así conseguir lo pedido. Ahora, determinamos el área de la figura:  asdf2.png ( 51.74k )
Número de descargas: 5
asdf2.png ( 51.74k )
Número de descargas: 5como vemos en la figura, para determinar el área sombreadad, sólo debemos determinar el doble del área de un triángulo equilátero de lado r, y dos sectores circulares de arco de 60º (o equivalentemente, uno de 120º): 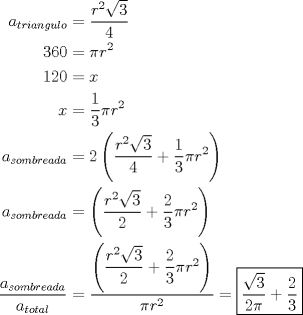 créditos a gastón por la ayuda con el tex xd espero esté bien el desarrollo -------------------- Estudia para superarte a ti mismo, no al resto. |
|
|
|
 Feb 20 2009, 02:13 PM Feb 20 2009, 02:13 PM
Publicado:
#10
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad:  Colegio/Liceo:  Sexo:  |
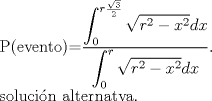
Mensaje modificado por Kaissa el Feb 20 2009, 02:19 PM -------------------- |
|
|
|
  |
2 usuario(s) está(n) leyendo esta discusión (2 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 23rd November 2024 - 05:02 PM |













![TEX: % MathType!MTEF!2!1!+-<br />% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaaca<br />% qGdbGaaeyyaiaabohacaqGVbGaae4CaiaabccacaqGMbGaaeyyaiaa<br />% bAhacaqGVbGaaeOCaiaabggacaqGIbGaaeiBaiaabwgacaqGZbaaba<br />% Gaae4qaiaabggacaqGZbGaae4BaiaabohacaqGGaGaaeiuaiaab+ga<br />% caqGZbGaaeyAaiaabkgacaqGSbGaaeyzaiaabohaaaGaeyOKH46aaS<br />% aaaeaacqaHapaCdaqadaqaamaalaaabaGaamOCamaakaaabaGaaGOm<br />% aaWcbeaaaOqaaiaaikdaaaaacaGLOaGaayzkaaWaaWbaaSqabeaaca<br />% aIYaaaaaGcbaGaeqiWda3aaeWaaeaacaWGYbaacaGLOaGaayzkaaWa<br />% aWbaaSqabeaacaaIYaaaaaaakiabg2da9maalaaabaWaaSaaaeaaca<br />% aIYaGaamOCamaaCaaaleqabaGaaGOmaaaaaOqaaiaaisdaaaaabaGa<br />% amOCamaaCaaaleqabaGaaGOmaaaaaaGccqGH9aqpdaWcaaqaamaala<br />% aabaGaamOCamaaCaaaleqabaGaaGOmaaaaaOqaaiaaikdaaaaabaGa<br />% amOCamaaCaaaleqabaGaaGOmaaaaaaGccqGH9aqpdaqjEaqaamaala<br />% aabaGaaGymaaqaaiaaikdaaaaaaaaa!6DF7!<br />\[<br />\frac{{{\text{Casos favorables}}}}<br />{{{\text{Casos Posibles}}}} \to \frac{{\pi \left( {\frac{{r\sqrt 2 }}<br />{2}} \right)^2 }}<br />{{\pi \left( r \right)^2 }} = \frac{{\frac{{2r^2 }}<br />{4}}}<br />{{r^2 }} = \frac{{\frac{{r^2 }}<br />{2}}}<br />{{r^2 }} = \boxed{\frac{1}<br />{2}}<br />\]<br />](./tex/cc5f3e278b383607acd9e60674436b97.png)
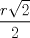 ?
?![TEX: \[<br />\begin{gathered}<br /> {\text{la probabilidad es igual al couciente entre el perimetro CIRCULAR}} \hfill \\<br /> {\text{del pedazo celeste y perimetro total de la circunferencia}} \hfill \\<br /> \frac{2}<br />{3} \hfill \\ <br />\end{gathered} <br />\]](./tex/d0bf8bb21bd33db438dbea35c1dc6ad2.png)

