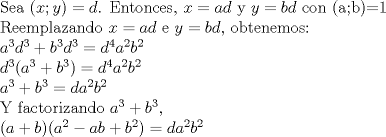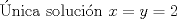|
|
|
|
|
|
|
  |
 Feb 11 2009, 05:49 PM Feb 11 2009, 05:49 PM
Publicado:
#1
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 836 Registrado: 9-January 07 Desde: Santiasko Miembro Nº: 3.659 Nacionalidad:  Sexo:  |
Resuelva en
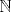 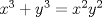 cualquiera puede responder! |
|
|
|
 Feb 11 2009, 06:53 PM Feb 11 2009, 06:53 PM
Publicado:
#2
|
|
|
Principiante Matemático Grupo: Usuario FMAT Mensajes: 3 Registrado: 22-January 09 Desde: Concepción Miembro Nº: 42.436 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Me siento tonta... no logro razonar... igual eta bueno el problemita... |
|
|
|
 Feb 11 2009, 11:23 PM Feb 11 2009, 11:23 PM
Publicado:
#3
|
|
 Dios Matemático Grupo: Team Ensayos FMAT Mensajes: 309 Registrado: 2-December 08 Desde: Cerro Navia Miembro Nº: 40.183 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Solución:
![TEX: <br />\[<br />\begin{gathered}<br /> {\text{Sea }}x = k \cdot y,{\text{ (con }}k \in N{\text{) el cambio de variable a usar}}{\text{.}} \hfill \\<br /> \hfill \\<br /> \Rightarrow (ky)^3 + y^3 = (ky)^2 y^2 \hfill \\<br /> \Rightarrow (k^3 + 1)y^3 = (k^2 )y^4 \hfill \\<br /> \hfill \\<br /> {\text{Como estamos buscando soluciones enteras, podemos afirmar que }}y \ne 0. \hfill \\<br /> \Rightarrow (k^3 + 1) = (k^2 )y \hfill \\<br /> \hfill \\<br /> {\text{Despejando }}y{\text{ se obtiene:}} \hfill \\<br /> \hfill \\<br /> y = \frac{{k^3 + 1}}<br />{{k^2 }} = k + \frac{1}<br />{{k^2 }} \hfill \\<br /> \hfill \\<br /> {\text{Luego, el valor de }}x{\text{ est\'a dado por:}} \hfill \\<br /> \hfill \\<br /> x = k \cdot (k + \frac{1}<br />{{k^2 }}) = k^2 + \frac{1}<br />{k} \hfill \\<br /> \hfill \\<br /> {\text{Finalmente el conjunto soluci\'on est\'a dado por:}} \hfill \\<br /> \hfill \\<br /> {\text{(x, y) = (}}k^2 + \frac{1}<br />{k},k + \frac{1}<br />{{k^2 }}{\text{)}} \hfill \\<br /> \hfill \\<br /> {\text{Y como se nos est\'a pidiendo soluciones naturales, se tiene que dar:}} \hfill \\<br /> \hfill \\<br /> \frac{1}<br />{k},\frac{1}<br />{{k^2 }} \in N{\text{ (y esto se logra solamente cuando }}k = 1{\text{)}}{\text{.}} \hfill \\<br /> \hfill \\<br /> {\text{Por lo tanto la soluci\'on buscada es: (x, y) = (2,2)}}{\text{.}} \hfill \\<br /> \hfill \\<br /> {\text{Salu2}}{\text{.}} \hfill \\ <br />\end{gathered} <br />\]](./tex/4774402f52bb4a50365188b426064277.png) |
|
|
|
 Feb 12 2009, 12:05 PM Feb 12 2009, 12:05 PM
Publicado:
#4
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Estás diciendo que todas las soluciones son de la forma (ky,y), con k natural. Es decir: estás diciendo que x debe ser múltiplo de y.
No estás justificando esa suposición, por lo tanto todavía esperamos una solución para el problema -------------------- |
|
|
|
 Feb 12 2009, 12:14 PM Feb 12 2009, 12:14 PM
Publicado:
#5
|
|
 Dios Matemático Grupo: Team Ensayos FMAT Mensajes: 309 Registrado: 2-December 08 Desde: Cerro Navia Miembro Nº: 40.183 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Estás diciendo que todas las soluciones son de la forma (ky,y), con k natural. Es decir: estás diciendo que x debe ser múltiplo de y. No estás justificando esa suposición, por lo tanto todavía esperamos una solución para el problema Justificación: Caso 1: Si x e y son impares: Este caso no puede ocurrir ya que 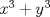 sería par, y sería par, y 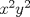 sería impar. sería impar.Caso 2: x par, y impar (S.P.G): Este caso no puede ocurrir ya que 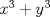 sería impar, y sería impar, y 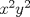 sería par. sería par.Luego el único caso posible de solución es que x e y sean pares. Luego es posible encontrar un 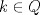 (sorry), que cumple la propiedad de que (sorry), que cumple la propiedad de que 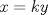 Pd: Creo que con eso debe quedar claro. Saludos. |
|
|
|
 Dec 3 2009, 05:44 PM Dec 3 2009, 05:44 PM
Publicado:
#6
|
|
|
Principiante Matemático Grupo: Usuario FMAT Mensajes: 12 Registrado: 27-July 09 Miembro Nº: 56.040 Nacionalidad:  Sexo:  |
|
|
|
|
 Dec 3 2009, 10:00 PM Dec 3 2009, 10:00 PM
Publicado:
#7
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 532 Registrado: 19-October 08 Desde: Santa Cruz de la Sierra Miembro Nº: 36.531 Nacionalidad:  Sexo:  |
la solucion esta correcta, bienvenido al foro
-------------------- "I've never let my school interfere with my education.”
|
|
|
|
 Feb 20 2010, 12:30 AM Feb 20 2010, 12:30 AM
Publicado:
#8
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 688 Registrado: 8-November 09 Desde: Villarrica Miembro Nº: 61.657 Nacionalidad:  Colegio/Liceo:  Universidad: .png) Sexo:  |
Aca va otra respuesta,
 Saludos Mensaje modificado por Pedantic Anarchy el Mar 4 2010, 02:09 PM -------------------- yo no soy especial
a pesar que ella lo dijo tengo unos krk y un celular hechizo aún vácilo SFDK en el segundo piso y la frase final da igual la improviso |
|
|
|
 Mar 4 2010, 02:07 PM Mar 4 2010, 02:07 PM
Publicado:
#9
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 688 Registrado: 8-November 09 Desde: Villarrica Miembro Nº: 61.657 Nacionalidad:  Colegio/Liceo:  Universidad: .png) Sexo:  |
.
Mensaje modificado por Pedantic Anarchy el Apr 3 2010, 03:55 PM -------------------- yo no soy especial
a pesar que ella lo dijo tengo unos krk y un celular hechizo aún vácilo SFDK en el segundo piso y la frase final da igual la improviso |
|
|
|
 Dec 28 2011, 02:20 PM Dec 28 2011, 02:20 PM
Publicado:
#10
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 532 Registrado: 19-October 08 Desde: Santa Cruz de la Sierra Miembro Nº: 36.531 Nacionalidad:  Sexo:  |
Aqui otra solucion:
Supongamos que  y y 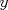 son distintos, entonces existe un primo son distintos, entonces existe un primo 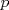 tal que tal que 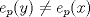 , y wlog que , y wlog que 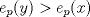 . Entonces . Entonces 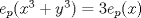 y y 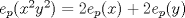 . Entonces . Entonces 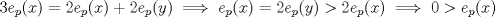 , contradiccion. Asi que , contradiccion. Asi que 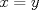 de donde trivialmente de donde trivialmente 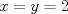
-------------------- "I've never let my school interfere with my education.”
|
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 3rd April 2025 - 04:25 PM |