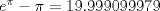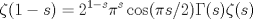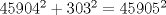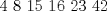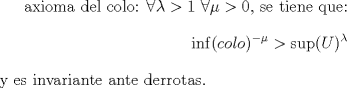|
|
|
|
|
|
|
  |
 Feb 7 2009, 12:38 PM Feb 7 2009, 12:38 PM
Publicado:
#1
|
|
|
Dios Matemático Supremo Grupo: Baneado Mensajes: 3.360 Registrado: 11-March 08 Miembro Nº: 16.617 |
  Editado Mensaje modificado por vivanco el Feb 7 2009, 01:07 PM |
|
|
|
 Feb 7 2009, 12:40 PM Feb 7 2009, 12:40 PM
Publicado:
#2
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.139 Registrado: 11-June 08 Desde: UK Miembro Nº: 26.837 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
que pasa con
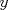 ? ?
-------------------- blep
|
|
|
|
 Feb 7 2009, 01:36 PM Feb 7 2009, 01:36 PM
Publicado:
#3
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.139 Registrado: 11-June 08 Desde: UK Miembro Nº: 26.837 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
notar que esta desigualdad es bastante parecida a :
bastara tomar 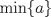 y generalizar y generalizar
Mensaje modificado por snw el Feb 7 2009, 01:39 PM -------------------- blep
|
|
|
|
 Feb 8 2009, 06:57 PM Feb 8 2009, 06:57 PM
Publicado:
#4
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.139 Registrado: 11-June 08 Desde: UK Miembro Nº: 26.837 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
bueno como no han pescado mi indicacion daré el resultado...
tomemos 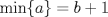 entonces: entonces:![TEX: $\dfrac{1+b(1+\dfrac{x}{b})}{b+1}\ge \sqrt[b+1]{\left(1+\dfrac{x}{b}\right)^b}\Rightarrow \left(1+\dfrac{x}{b+1}\right)^{b+1}\ge \left(1+\dfrac{x}{b}\right)^b$](./tex/4a112f50375fbb343312e91045a3cc5e.png) Luego si 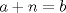 con con 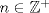 haciendo un procedimiento analogo se tendrá que: haciendo un procedimiento analogo se tendrá que: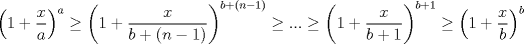 Finalmente por transitividad se concluye lo pedido -------------------- blep
|
|
|
|
 Feb 26 2016, 05:19 AM Feb 26 2016, 05:19 AM
Publicado:
#5
|
|
|
Maestro Matemático Grupo: Usuario FMAT Mensajes: 133 Registrado: 9-June 15 Desde: Valporro - Puerto Ron Miembro Nº: 138.365 Nacionalidad:  Universidad:  Sexo:  |
![TEX: Consideremos la función $f: (0, \infty) \rightarrow \mathbb{R}$ dada por $f(t)= \left(1+ \dfrac{x}{t} \right)^{t}$, con $x>0$.<br />Derivando $f$ respecto a $t$ se tiene que \\$f'(t)=\left(1+ \dfrac{x}{t} \right)^{t}\cdot \left[Ln \left(1+\dfrac{x}{t} \right)-\dfrac{t}{x+t} \right].$](/tex-image/590c3581fe106b2b1bc3bfcf319dff90.png) 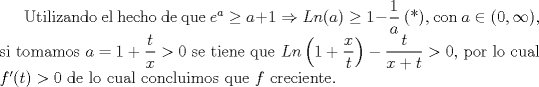   |
|
|
|
 Feb 26 2016, 12:34 PM Feb 26 2016, 12:34 PM
Publicado:
#6
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.879 Registrado: 27-December 07 Desde: ∂Ω©ȹʕѺϧگἐᾋ1©Ӹ█₯►☻X TH.....I FORGOR Miembro Nº: 14.122 Nacionalidad:  Universidad:  Sexo:  |
En realidad hay que repetir lo indicado por snw.
Note que como a>b y x>0: 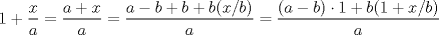 Y por MA-MG: 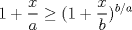 GG IZI. Saludos Claudio. PD: igual la derivada salva, pero se siente como si jugaras GTA usando trampa. La idea de las desigualdades es tratar de no usar calculo salvo cuando sea estrictamente necesario. -------------------- Claudio Henriquez Tapia Ingeniero Civil Matemático UTFSM y Prof. DMAT UTFSM Candidato a Doctor en Estadística UC. Campus San Joaquin Si todo sale bien, estaría defendiendo en Julio 2024. [indent] everywhere at the end of FMAT fmat needs .... To Survive... 3ch03s facts: Frases para el bronce by 3ch03s: Fmat dejame subir mas citas! TB-3030303 que es YTP-Tennis: |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 3rd April 2025 - 11:06 PM |