parecida a cauchy - Foro fmat.cl

parecida a cauchy, pero no...

snw Ver Perfil del Miembro Ver los mensajes de este miembro	Feb 5 2009, 09:05 AM Publicado: #1
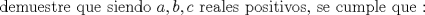Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.139 Registrado: 11-June 08 Desde: UK Miembro Nº: 26.837 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	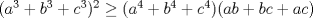$TEX: demuestre que siendo $a,b,c$ reales positivos, se cumple que :$ $TEX: $(a^3+b^3+c^3)^2\ge (a^4+b^4+c^4)(ab+bc+ac)$$ saludos, perdón si ya está -------------------- blep

mamboraper Ver Perfil del Miembro Ver los mensajes de este miembro	Feb 16 2018, 06:52 PM Publicado: #2
Maestro Matemático Grupo: Usuario FMAT Mensajes: 134 Registrado: 28-March 14 Miembro Nº: 128.100 Nacionalidad: Sexo:	$TEX: Por Muirhead tenemos que $(3,3,0)>(1,5,0)$: $$\Rightarrow 2(a^3b^3 + b^3c^3 + a^3c^3)\geq a^5b + ab^5 + b^5c + bc^5 + a^5c + ac^5 \ \text{(i)}$$ Además $(6,0,0)>(4,1,1)$: $$a^6 + b^6 + c^6 \geq a^4bc + ab^4c + abc^4 \ \text{(ii)}$$ sumando (i) y (ii) y factorizando obtenemos: $$(a^3 + b^3 + c^3)^2\geq (ab+bc+ac)(a^4 + b^4 + c^4) \ \blacksquare$$$ -------------------- Hago clases particulares (activo 2024). Cualquier consulta por MP.

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Fecha y Hora actual: 23rd November 2024 - 06:53 AM