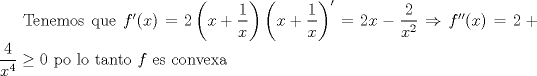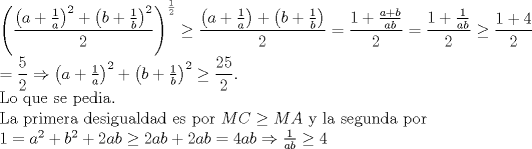Una clasica - Foro fmat.cl

Una clasica, No se si este

xdanielx Ver Perfil del Miembro Ver los mensajes de este miembro	Feb 3 2009, 12:18 PM Publicado: #1
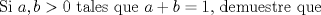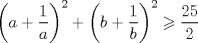Dios Matemático Supremo Grupo: Baneado Mensajes: 3.360 Registrado: 11-March 08 Miembro Nº: 16.617	$TEX: Si $a,b > 0$ tales que $a + b = 1$, demuestre que$ $TEX: $$<br />\left( {a + \frac{1}<br />{a}} \right)^2 + \left( {b + \frac{1}<br />{b}} \right)^2 \geqslant \frac{{25}}<br />{2}<br />$$$

snw Ver Perfil del Miembro Ver los mensajes de este miembro	Feb 23 2009, 12:02 AM Publicado: #2
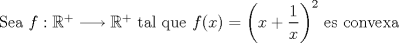Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.139 Registrado: 11-June 08 Desde: UK Miembro Nº: 26.837 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: Sea $f:{\Bbb R^+}\longrightarrow{\Bbb R^+}$ tal que $f(x)=\left(x+\dfrac{1}{x}\right)^2$ es convexa$ dem: $TEX: Tenemos que $f'(x)=2\left(x+\dfrac{1}{x}\right)\left(x+\dfrac{1}{x}\right)'=2x-\dfrac{2}{x^2}\Rightarrow f''(x)=2+\dfrac{4}{x^4}\ge 0$ po lo tanto $f$ es convexa$ $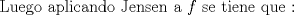TEX: Luego aplicando Jensen a $f$ se tiene que :$ $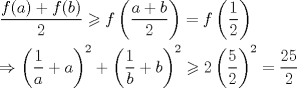TEX: <br />$<br />\begin{gathered}<br /> \dfrac{f(a) + f(b)}{2} \geqslant f\left( {\frac{{a + b}}<br />{2}} \right) = f\left( {\frac{1}<br />{2}} \right) \hfill \\<br />\Rightarrow \left( {\frac{1}<br />{a} + a} \right)^2 + \left( {\frac{1}<br />{b} + b} \right)^2 \geqslant 2\left( {\frac{5}<br />{2}} \right)^2 = \frac{{25}}<br />{2} \hfill \\ <br />\end{gathered} <br />$<br />$ Que es lo que se queria probar Mensaje modificado por snw el Feb 23 2009, 11:07 AM -------------------- blep

the return of Ver Perfil del Miembro Ver los mensajes de este miembro	Mar 31 2009, 03:57 PM Publicado: #3
Principiante Matemático Grupo: Usuario FMAT Mensajes: 5 Registrado: 31-March 09 Miembro Nº: 46.646 Nacionalidad: Sexo:	CITA(vivanco @ Feb 3 2009, 01:18 PM) $TEX: Si $a,b > 0$ tales que $a + b = 1$, demuestre que$ $TEX: $$<br />\left( {a + \frac{1}<br />{a}} \right)^2 + \left( {b + \frac{1}<br />{b}} \right)^2 \geqslant \frac{{25}}<br />{2}<br />$$$ $TEX: \noindent $\left(\dfrac{\left( a+\frac{1}{a}\right)^2+\left( b+\frac{1}{b} \right)^2}{2}\right)^{\frac{1}{2}}\ge \dfrac{\left(a+\frac{1}{a}\right)+\left(b+\frac{1}{b}\right)}{2}=\dfrac{1+\frac{a+b}{ab}}{2}=\dfrac{1+\frac{1}{ab}}{2}\ge \dfrac{1+4}{2}\\<br />=\dfrac{5}{2}\Rightarrow \left( a+\frac{1}{a}\right)^2+\left( b+\frac{1}{b} \right)^2\ge \dfrac{25}{2}$.\\<br />Lo que se pedia.\\<br />La primera desigualdad es por $MC\ge MA$ y la segunda por \\<br />$1=a^2+b^2+2ab\ge 2ab+2ab=4ab\Rightarrow \frac{1}{ab}\ge 4$$

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Fecha y Hora actual: 23rd November 2024 - 04:03 PM