 Reparametrización por longitud |
|
|
|
|
|
|
Foro fmat.cl > Programa Enseñanza Universitaria > Consultas > Banco de Problemas Resueltos > Cálculo > Cálculo Vectorial  |
 Jan 28 2009, 05:54 PM
Publicado:
#1
|
|
|
Maestro Matemático  Grupo: Usuario FMAT Mensajes: 109 Registrado: 25-February 08 Miembro Nº: 15.863  |
Reparametrizar:
![TEX: <br /><br />\[<br />r(t) = e^t senti + e^t \cos tj<br />\]<br />](./tex/5ca43d4305ffc322bf5a696bd7a08a18.png) en t = 0 Mmmm... lo hice, pero me da un resultado nada que ver a lo que está en el libro... Obtuve r'(t) y luego apliqué la formulita: ![TEX: \[<br />\int\limits_0^t {2e^x \cos xdx = \cos xe^x } \left| {_0^t + senxe^x } \right.\left| {_0^t } \right.<br />\]<br />](./tex/c11e34a308f687576f12cd36f18ee906.png) Ahí apliqué integración por partes (quizás en eso me equivoqué) y resulta que t me da t = ln(s+1) pero según el libro no es eso  gracias Mensaje modificado por ÑAKA el Jan 28 2009, 05:54 PM |
 |
 
|
|
Jan 28 2009, 06:49 PM
Publicado:
#2
|
|
 Dios Matemático Supremo  Grupo: Colaborador Platinum Mensajes: 824 Registrado: 15-October 07 Desde: Valparaíso Miembro Nº: 11.342 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Calculaste mal la norma de
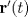 .![TEX: \[<br />\begin{gathered}<br /> {\mathbf{r}}'(t) = e^t \left( {\sin t + \cos t} \right){\mathbf{i}} + e^t \left( {\cos t - \sin t} \right){\mathbf{j}} \hfill \\<br /> \Rightarrow \left\| {{\mathbf{r}}'(t)} \right\| = \sqrt {e^{2t} \left( {\sin ^2 t + 2\sin t\cos t + \cos ^2 t} \right) + e^{2t} \left( {\sin ^2 t - 2\sin t\cos t + \cos ^2 t} \right)} = e^t \sqrt 2 \hfill \\ <br />\end{gathered} <br />\]<br /><br />](./tex/fd91418438f5224030fdc6d519b14fd6.png) Saludos -------------------- Pedro P. Montero Silva Estudiante de Licenciatura en Ciencias, Mención Matemática - Mechón 2009 "One rather curious conclusion emerges, that pure mathematics is on the whole distinctly more useful than applied. A pure mathematician seems to have the advantage on the practical as well as on the aesthetic side. For what is useful above all is technique, and mathematical technique is taught mainly through pure mathematics." G.H. Hardy |
|
|
|
|
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 23rd November 2024 - 07:35 PM |
